//<p>给定一个由非重叠的轴对齐矩形的数组 <code>rects</code> ，其中 <code>rects[i] = [ai, bi, xi, yi]</code> 表示 <code>(ai, bi)</code> 是第 <code>i</code> 个矩形的左下角点，<code>(xi, yi)</code> 是第 <code>i</code> 个矩形的右上角点。设计一个算法来随机挑选一个被某一矩形覆盖的整数点。矩形周长上的点也算做是被矩形覆盖。所有满足要求的点必须等概率被返回。</p>
//
//<p>在给定的矩形覆盖的空间内的任何整数点都有可能被返回。</p>
//
//<p><strong>请注意&nbsp;</strong>，整数点是具有整数坐标的点。</p>
//
//<p>实现&nbsp;<code>Solution</code>&nbsp;类:</p>
//
//<ul>
//	<li><code>Solution(int[][] rects)</code>&nbsp;用给定的矩形数组&nbsp;<code>rects</code> 初始化对象。</li>
//	<li><code>int[] pick()</code>&nbsp;返回一个随机的整数点 <code>[u, v]</code> 在给定的矩形所覆盖的空间内。</li>
//</ul>
//
//<ol>
//</ol>
//
//<p>&nbsp;</p>
//
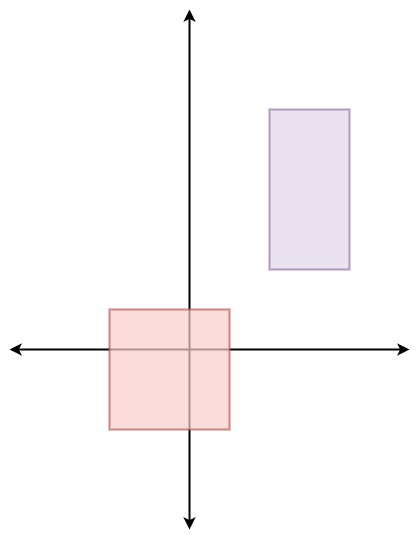
//<p><strong>示例 1：</strong></p>
//
//<p><img src="https://assets.leetcode.com/uploads/2021/07/24/lc-pickrandomrec.jpg" style="height: 539px; width: 419px;" /></p>
//
//<pre>
//<strong>输入: 
//</strong>["Solution", "pick", "pick", "pick", "pick", "pick"]
//[[[[-2, -2, 1, 1], [2, 2, 4, 6]]], [], [], [], [], []]
//<strong>输出: 
//</strong>[null, [1, -2], [1, -1], [-1, -2], [-2, -2], [0, 0]]
//
//<strong>解释：</strong>
//Solution solution = new Solution([[-2, -2, 1, 1], [2, 2, 4, 6]]);
//solution.pick(); // 返回 [1, -2]
//solution.pick(); // 返回 [1, -1]
//solution.pick(); // 返回 [-1, -2]
//solution.pick(); // 返回 [-2, -2]
//solution.pick(); // 返回 [0, 0]</pre>
//
//<p>&nbsp;</p>
//
//<p><strong>提示：</strong></p>
//
//<ul>
//	<li><code>1 &lt;= rects.length &lt;= 100</code></li>
//	<li><code>rects[i].length == 4</code></li>
//	<li><code>-10<sup>9</sup>&nbsp;&lt;= a<sub>i</sub>&nbsp;&lt; x<sub>i</sub>&nbsp;&lt;= 10<sup>9</sup></code></li>
//	<li><code>-10<sup>9</sup>&nbsp;&lt;= b<sub>i</sub>&nbsp;&lt; y<sub>i</sub>&nbsp;&lt;= 10<sup>9</sup></code></li>
//	<li><code>x<sub>i</sub>&nbsp;- a<sub>i</sub>&nbsp;&lt;= 2000</code></li>
//	<li><code>y<sub>i</sub>&nbsp;- b<sub>i</sub>&nbsp;&lt;= 2000</code></li>
//	<li>所有的矩形不重叠。</li>
//	<li><code>pick</code> 最多被调用&nbsp;<code>10<sup>4</sup></code>&nbsp;次。</li>
//</ul>
//<div><div>Related Topics</div><div><li>水塘抽样</li><li>数学</li><li>二分查找</li><li>有序集合</li><li>前缀和</li><li>随机化</li></div></div><br><div><li>👍 98</li><li>👎 0</li></div>
package leetcode.editor.cn;

import java.util.Random;

// 497:非重叠矩形中的随机点
public class RandomPointInNonOverlappingRectangles {
    public static void main(String[] args) {
        // TO TEST
    }

    //leetcode submit region begin(Prohibit modification and deletion)
    class Solution {
        int[][] rects;
        int[] mul;
        int count;
        Random random = new Random();

        public Solution(int[][] rects) {
            this.rects = rects;
            count = this.rects.length;
            mul = new int[count + 1];
            for (int i = 1; i <= count; i++) {
                mul[i] = mul[i - 1] + (this.rects[i - 1][2] - this.rects[i - 1][0] + 1) *
                        (this.rects[i - 1][3] - this.rects[i - 1][1] + 1);
            }
        }

        public int[] pick() {
            int index = random.nextInt(mul[count]) + 1;
            int left = 0;
            int right = count;
            while (left < right) {
                int mid = left + right >> 1;
                if (mul[mid] >= index) {
                    right = mid;
                } else {
                    left = mid + 1;
                }
            }
            return new int[]{
                    random.nextInt(rects[right - 1][2] - rects[right - 1][0] + 1) + rects[right - 1][0],
                    random.nextInt(rects[right - 1][3] - rects[right - 1][1] + 1) + rects[right - 1][1]
            };
        }
    }

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(rects);
 * int[] param_1 = obj.pick();
 */
//leetcode submit region end(Prohibit modification and deletion)

}