修改忽略文件
This commit is contained in:
parent
c8ddb46c9d
commit
d1a180bbab
2
.gitignore
vendored
2
.gitignore
vendored
@ -3,5 +3,3 @@
|
||||
/src/test/
|
||||
/target/
|
||||
/src/main/java/leetcode/editor/cn/*.txt
|
||||
/src/main/java/leetcode/editor/cn/doc/solution/
|
||||
/src/main/java/leetcode/editor/cn/doc/submission/
|
||||
|
||||
@ -0,0 +1,48 @@
|
||||
### 解题思路
|
||||
|
||||
f(s,i) 表示字符串s从i开始的大小写变化结果。
|
||||
|
||||
大小写一致时候返回一组结果
|
||||
否则返回两组结果
|
||||
|
||||
by 瓦片
|
||||
|
||||
### 代码
|
||||
|
||||
* java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public List<String> letterCasePermutation(String s) {
|
||||
return f(s, 0);
|
||||
}
|
||||
|
||||
private List<String> f(String s, int i) {
|
||||
List<String> result = new ArrayList<>();
|
||||
if (i == s.length() -1 ) {
|
||||
String s1 = ("" + s.charAt(i)).toLowerCase();
|
||||
String s2 = ("" + s.charAt(i)).toUpperCase();
|
||||
if(s1.equals(s2)) {
|
||||
result.add(s1);
|
||||
}else {
|
||||
result.add(s1);
|
||||
result.add(s2);
|
||||
}
|
||||
} else {
|
||||
List<String> rest = f(s, i + 1);
|
||||
String s1 = ("" + s.charAt(i)).toLowerCase();
|
||||
String s2 = ("" + s.charAt(i)).toUpperCase();
|
||||
for (String r : rest) {
|
||||
if(s1.equals(s2)) {
|
||||
result.add(s1 + r);
|
||||
}else {
|
||||
result.add(s1 + r);
|
||||
result.add(s2 + r);
|
||||
}
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -0,0 +1,50 @@
|
||||
## 题解
|
||||
|
||||
显然,如果洗衣机的数量 不能整除 所有洗衣机的衣服之和,则不能使每台洗衣机中衣物的数量相等。
|
||||
|
||||
反之,都可以使每台洗衣机中衣物的数量相等。
|
||||
|
||||
**每台洗衣机,每次只能将一件衣服送到相邻的一台洗衣机。**
|
||||
|
||||
设 $Max=max_{i=0}^{n-1} machine[i]$, 即所有洗衣机中最多的衣服数量,$Avg=\frac{\sum_{i=0}^{n-1}machine[i]}{n}$ 等于最后每台洗衣机中衣物的数量相等的数量。
|
||||
|
||||
- 因为每次只能移动一件衣服,所有对于衣服数量最多的一个洗衣机,最少需要 $Max - Avg$ 次转移。
|
||||
- 因为每次只能往相邻的洗衣机转移一件衣服,所以假设前 $i$ 个洗衣机的衣服总和为 $sum$,那么至少需要 $|sum - i * Avg|$ 次转移,才能使 前$i$个 和 前$i$个后面 洗衣机中的衣服相等。若 $sum - i * Avg>0$ 则表示 前$i$个洗衣机的衣服,需要向 前$i$个洗衣机后面里 转移;,若 $sum - i * Avg<=0$ 则表示 前$i$个后面的洗衣机的衣服,需要向 前$i$个洗衣机里 转移。
|
||||
|
||||
两者情况取最大值。
|
||||
|
||||
时间复杂度: $O(n)$。
|
||||
|
||||
空间复杂度: $O(1)$。
|
||||
|
||||
## 代码
|
||||
|
||||
* c++
|
||||
|
||||
```c++
|
||||
class Solution {
|
||||
public:
|
||||
int findMinMoves(vector<int>& machines) {
|
||||
int ans = 0, sum = 0, presum = 0;
|
||||
for (int i = 0; i < machines.size(); i++)
|
||||
sum += machines[i];
|
||||
|
||||
if (sum % machines.size() != 0)
|
||||
return -1;
|
||||
|
||||
int avg = sum / machines.size();
|
||||
|
||||
for (int i = 0; i < machines.size(); i++) {
|
||||
presum += machines[i];
|
||||
ans = max(ans, max(machines[i] - avg, abs(presum - avg * (i + 1))));
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||

|
||||
|
||||
## 最后
|
||||
|
||||
大家好,我是编程熊,字节跳动、旷视科技前员工,ACM亚洲区域赛金牌,欢迎 [关注我](https://leetcode-cn.com/u/bianchengxiong/)
|
||||
@ -0,0 +1,237 @@
|
||||
#### 方法一:前缀和 + 二分查找
|
||||
|
||||
**思路与算法**
|
||||
|
||||
设数组 $w$ 的权重之和为 $\textit{total}$。根据题目的要求,我们可以看成将 $[1, \textit{total}]$ 范围内的所有整数分成 $n$ 个部分(其中 $n$ 是数组 $w$ 的长度),第 $i$ 个部分恰好包含 $w[i]$ 个整数,并且这 $n$ 个部分两两的交集为空。随后我们在 $[1, \textit{total}]$ 范围内随机选择一个整数 $x$,如果整数 $x$ 被包含在第 $i$ 个部分内,我们就返回 $i$。
|
||||
|
||||
一种较为简单的划分方法是按照从小到大的顺序依次划分每个部分。例如 $w = [3, 1, 2, 4]$ 时,权重之和 $\textit{total} = 10$,那么我们按照 $[1, 3], [4, 4], [5, 6], [7, 10]$ 对 $[1, 10]$ 进行划分,使得它们的长度恰好依次为 $3, 1, 2, 4$。可以发现,每个区间的左边界是在它之前出现的所有元素的和加上 $1$,右边界是到它为止的所有元素的和。因此,如果我们用 $\textit{pre}[i]$ 表示数组 $w$ 的前缀和:
|
||||
|
||||
$$
|
||||
\textit[i] = \sum_^i w[k]
|
||||
$$
|
||||
|
||||
那么第 $i$ 个区间的左边界就是 $\textit{pre}[i] - w[i] + 1$,右边界就是 $\textit{pre}[i]$。
|
||||
|
||||
当划分完成后,假设我们随机到了整数 $x$,我们希望找到满足:
|
||||
|
||||
$$
|
||||
\textit[i] - w[i] + 1 \leq x \leq \textit[i]
|
||||
$$
|
||||
|
||||
的 $i$ 并将其作为答案返回。由于 $\textit{pre}[i]$ 是单调递增的,因此我们可以使用二分查找在 $O(\log n)$ 的时间内快速找到 $i$,即找出最小的满足 $x \leq \textit{pre}[i]$ 的下标 $i$。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
mt19937 gen;
|
||||
uniform_int_distribution<int> dis;
|
||||
vector<int> pre;
|
||||
|
||||
public:
|
||||
Solution(vector<int>& w): gen(random_device{}()), dis(1, accumulate(w.begin(), w.end(), 0)) {
|
||||
partial_sum(w.begin(), w.end(), back_inserter(pre));
|
||||
}
|
||||
|
||||
int pickIndex() {
|
||||
int x = dis(gen);
|
||||
return lower_bound(pre.begin(), pre.end(), x) - pre.begin();
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
int[] pre;
|
||||
int total;
|
||||
|
||||
public Solution(int[] w) {
|
||||
pre = new int[w.length];
|
||||
pre[0] = w[0];
|
||||
for (int i = 1; i < w.length; ++i) {
|
||||
pre[i] = pre[i - 1] + w[i];
|
||||
}
|
||||
total = Arrays.stream(w).sum();
|
||||
}
|
||||
|
||||
public int pickIndex() {
|
||||
int x = (int) (Math.random() * total) + 1;
|
||||
return binarySearch(x);
|
||||
}
|
||||
|
||||
private int binarySearch(int x) {
|
||||
int low = 0, high = pre.length - 1;
|
||||
while (low < high) {
|
||||
int mid = (high - low) / 2 + low;
|
||||
if (pre[mid] < x) {
|
||||
low = mid + 1;
|
||||
} else {
|
||||
high = mid;
|
||||
}
|
||||
}
|
||||
return low;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
int[] pre;
|
||||
int total;
|
||||
Random ran = new Random();
|
||||
|
||||
public Solution(int[] w) {
|
||||
pre = new int[w.Length];
|
||||
pre[0] = w[0];
|
||||
for (int i = 1; i < w.Length; ++i) {
|
||||
pre[i] = pre[i - 1] + w[i];
|
||||
}
|
||||
total = w.Sum();
|
||||
}
|
||||
|
||||
public int PickIndex() {
|
||||
int x = ran.Next(1, total + 1);
|
||||
return BinarySearch(x);
|
||||
}
|
||||
|
||||
private int BinarySearch(int x) {
|
||||
int low = 0, high = pre.Length - 1;
|
||||
while (low < high) {
|
||||
int mid = (high - low) / 2 + low;
|
||||
if (pre[mid] < x) {
|
||||
low = mid + 1;
|
||||
} else {
|
||||
high = mid;
|
||||
}
|
||||
}
|
||||
return low;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
|
||||
def __init__(self, w: List[int]):
|
||||
self.pre = list(accumulate(w))
|
||||
self.total = sum(w)
|
||||
|
||||
def pickIndex(self) -> int:
|
||||
x = random.randint(1, self.total)
|
||||
return bisect_left(self.pre, x)
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var Solution = function(w) {
|
||||
pre = new Array(w.length).fill(0);
|
||||
pre[0] = w[0];
|
||||
for (let i = 1; i < w.length; ++i) {
|
||||
pre[i] = pre[i - 1] + w[i];
|
||||
}
|
||||
this.total = _.sum(w);
|
||||
};
|
||||
|
||||
Solution.prototype.pickIndex = function() {
|
||||
const x = Math.floor((Math.random() * this.total)) + 1;
|
||||
const binarySearch = (x) => {
|
||||
let low = 0, high = pre.length - 1;
|
||||
while (low < high) {
|
||||
const mid = Math.floor((high - low) / 2) + low;
|
||||
if (pre[mid] < x) {
|
||||
low = mid + 1;
|
||||
} else {
|
||||
high = mid;
|
||||
}
|
||||
}
|
||||
return low;
|
||||
}
|
||||
return binarySearch(x);
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
type Solution struct {
|
||||
pre []int
|
||||
}
|
||||
|
||||
func Constructor(w []int) Solution {
|
||||
for i := 1; i < len(w); i++ {
|
||||
w[i] += w[i-1]
|
||||
}
|
||||
return Solution{w}
|
||||
}
|
||||
|
||||
func (s *Solution) PickIndex() int {
|
||||
x := rand.Intn(s.pre[len(s.pre)-1]) + 1
|
||||
return sort.SearchInts(s.pre, x)
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
typedef struct {
|
||||
int* pre;
|
||||
int preSize;
|
||||
int total;
|
||||
} Solution;
|
||||
|
||||
Solution* solutionCreate(int* w, int wSize) {
|
||||
Solution* obj = malloc(sizeof(Solution));
|
||||
obj->pre = malloc(sizeof(int) * wSize);
|
||||
obj->preSize = wSize;
|
||||
obj->total = 0;
|
||||
for (int i = 0; i < wSize; i++) {
|
||||
obj->total += w[i];
|
||||
if (i > 0) {
|
||||
obj->pre[i] = obj->pre[i - 1] + w[i];
|
||||
} else {
|
||||
obj->pre[i] = w[i];
|
||||
}
|
||||
}
|
||||
return obj;
|
||||
}
|
||||
|
||||
int binarySearch(Solution* obj, int x) {
|
||||
int low = 0, high = obj->preSize - 1;
|
||||
while (low < high) {
|
||||
int mid = (high - low) / 2 + low;
|
||||
if (obj->pre[mid] < x) {
|
||||
low = mid + 1;
|
||||
} else {
|
||||
high = mid;
|
||||
}
|
||||
}
|
||||
return low;
|
||||
}
|
||||
|
||||
int solutionPickIndex(Solution* obj) {
|
||||
int x = rand() % obj->total + 1;
|
||||
return binarySearch(obj, x);
|
||||
}
|
||||
|
||||
void solutionFree(Solution* obj) {
|
||||
free(obj->pre);
|
||||
free(obj);
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:初始化的时间复杂度为 $O(n)$,每次选择的时间复杂度为 $O(\log n)$,其中 $n$ 是数组 $w$ 的长度。
|
||||
|
||||
- 空间复杂度:$O(n)$,即为前缀和数组 $\textit{pre}$ 需要使用的空间。
|
||||
|
||||
@ -0,0 +1,64 @@
|
||||
# 核心思想:
|
||||
|
||||
依次遍历比较同位置上的字符是否相同,且数量必须为偶数。因为若不相同的数量为奇数,则肯定不能交换成相同的字符串;
|
||||
**证明:**
|
||||
若```[s1[i], s2[i]] == ["x", "y"]```的个数为n1,```[s1[i], s2[i]] == ["y", "x"]```的个数为n2;所以字符'x'和'y'的个数都为n1+n2。
|
||||
1. 当n1+n2为奇数时,字符'x'和'y'无法分配到两个字符串中,则肯定无法交换成为两个相同的字符串。
|
||||
2. 当n1+n2为偶数时,则可以通过交换两个字符串的字符使得两个字符串完全相等。
|
||||
|
||||
字符不相等分为两种情况讨论:
|
||||
s1 : "xy"
|
||||
s2 : "yx"
|
||||
和
|
||||
s1 : "xx"
|
||||
s2 : "yy"
|
||||
第一种需要交换两次才能都变成"xy"或"yx"。第二种则只需要交换一次即可。
|
||||
因此在遍历时分别统计这两种情况的数量,最后再统一计算需要交换的次数。
|
||||
|
||||
# 复杂度分析
|
||||
|
||||
时间复杂度:O(n), n为字符串的长度
|
||||
空间复杂度:O(1)
|
||||
|
||||
* []
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def minimumSwap(self, s1: str, s2: str) -> int:
|
||||
cnt1, cnt2 = 0, 0
|
||||
for i in range(len(s1)):
|
||||
if s1[i] == 'x' and s2[i] == 'y':
|
||||
cnt1 += 1
|
||||
elif s1[i] == 'y' and s2[i] == 'x':
|
||||
cnt2 += 1
|
||||
if (cnt1 + cnt2) % 2 != 0:
|
||||
return -1
|
||||
n1, m1 = divmod(cnt1, 2)
|
||||
n2, m2 = divmod(cnt2, 2)
|
||||
return n1 + n2 + 2 * m1
|
||||
```
|
||||
|
||||
* []
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int minimumSwap(string s1, string s2) {
|
||||
int cnt1 = 0;
|
||||
int cnt2 = 0;
|
||||
for (int i = 0; i < s1.size(); i++) {
|
||||
if (s1[i] == 'x' && s2[i] == 'y') {
|
||||
cnt1++;
|
||||
} else if (s1[i] == 'y' && s2[i] == 'x') {
|
||||
cnt2++;
|
||||
}
|
||||
}
|
||||
if ((cnt1 + cnt2) % 2 != 0) {
|
||||
return -1;
|
||||
}
|
||||
return cnt1 / 2 + cnt2 / 2 + 2 * (cnt1 % 2);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||

|
||||
@ -0,0 +1,124 @@
|
||||
## 概述
|
||||
|
||||
这篇文章是为初级读者准备的,文章中会介绍了以下几种方法和数据结构:
|
||||
线性搜索,二分搜索和散列表。
|
||||
|
||||
#### 方法一 (线性搜索) 【超时】
|
||||
|
||||
**思路**
|
||||
将每个元素与它之前的 $k$ 个元素中比较查看它们是否相等。
|
||||
|
||||
**算法**
|
||||
|
||||
这个算法维护了一个 $k$ 大小的滑动窗口,然后在这个窗口里面搜索是否存在跟当前元素相等的元素。
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
public boolean containsNearbyDuplicate(int[] nums, int k) {
|
||||
for (int i = 0; i < nums.length; ++i) {
|
||||
for (int j = Math.max(i - k, 0); j < i; ++j) {
|
||||
if (nums[i] == nums[j]) return true;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
// Time Limit Exceeded.
|
||||
```
|
||||
|
||||
**时间复杂度分析**
|
||||
|
||||
* 时间复杂度:$O(n \min(k,n))$
|
||||
每次搜索都要花费 $O(\min(k, n))$ 的时间,哪怕$k$比$n$大,一次搜索中也只需比较 $n$ 次。
|
||||
|
||||
* 空间复杂度:$O(1)$
|
||||
|
||||
#### 方法二 (二叉搜索树) 【超时】
|
||||
|
||||
**思路**
|
||||
|
||||
通过自平衡二叉搜索树来维护一个 $k$ 大小的滑动窗口。
|
||||
|
||||
**算法**
|
||||
|
||||
这个方法的核心在于降低方法一中搜索前 $k$ 个元素所耗费的时间。可以想一下,我们能不能用一个更复杂的数据结构来维持这个 $k$ 大小的滑动窗口内元素的有序性呢?考虑到滑动窗口内元素是严格遵守先进先出的,那么队列会是一个非常自然就能想到的数据结构。链表实现的队列可以支持在常数时间内的 `删除`,`插入`,然而 `搜索` 耗费的时间却是线性的,所以如果用队列来实现的话结果并不会比方法一更好。
|
||||
|
||||
一个更好的选择是使用自平衡二叉搜索树(BST)。 BST 中`搜索`,`删除`,`插入`都可以保持 $O(\log k)$ 的时间复杂度,其中 $k$ 是 BST 中元素的个数。在大部分面试中你都不需要自己去实现一个 BST,所以把 BST 当成一个黑盒子就可以了。大部分的编程语言都会在标准库里面提供这些常见的数据结构。在 Java 里面,你可以用 `TreeSet` 或者是 `TreeMap`。在 C++ STL 里面,你可以用 `std::set` 或者是 `std::map`。
|
||||
|
||||
假设你已经有了这样一个数据结构,伪代码是这样的:
|
||||
|
||||
* 遍历数组,对于每个元素做以下操作:
|
||||
* 在 BST 中搜索当前元素,如果找到了就返回 `true`。
|
||||
* 在 BST 中插入当前元素。
|
||||
* 如果当前 BST 的大小超过了 $k$,删除当前 BST 中最旧的元素。
|
||||
* 返回 `false`。
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
public boolean containsNearbyDuplicate(int[] nums, int k) {
|
||||
Set<Integer> set = new TreeSet<>();
|
||||
for (int i = 0; i < nums.length; ++i) {
|
||||
if (set.contains(nums[i])) return true;
|
||||
set.add(nums[i]);
|
||||
if (set.size() > k) {
|
||||
set.remove(nums[i - k]);
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
// Time Limit Exceeded.
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
* 时间复杂度:$O(n \log (\min(k,n)))$
|
||||
我们会做 $n$ 次 `搜索`,`删除`,`插入` 操作。每次操作将耗费对数时间,即为 $\log (\min(k, n))$。注意,虽然 $k$ 可以比 $n$ 大,但滑动窗口大小不会超过 $n$。
|
||||
|
||||
* 空间复杂度:$O(\min(n,k))$
|
||||
只有滑动窗口需要开辟额外的空间,而滑动窗口的大小不会超过 $O(\min(n,k))$。
|
||||
|
||||
**注意事项**
|
||||
|
||||
这个算法在 $n$ 和 $k$ 很大的时候依旧会超时。
|
||||
|
||||
#### 方法三 (散列表) 【通过】
|
||||
|
||||
**思路**
|
||||
|
||||
用散列表来维护这个$k$大小的滑动窗口。
|
||||
|
||||
**算法**
|
||||
|
||||
在之前的方法中,我们知道了对数时间复杂度的 `搜索` 操作是不够的。在这个方法里面,我们需要一个支持在常量时间内完成 `搜索`,`删除`,`插入` 操作的数据结构,那就是散列表。这个算法的实现跟方法二几乎是一样的。
|
||||
|
||||
* 遍历数组,对于每个元素做以下操作:
|
||||
* 在散列表中搜索当前元素,如果找到了就返回 `true`。
|
||||
* 在散列表中插入当前元素。
|
||||
* 如果当前散列表的大小超过了 $k$, 删除散列表中最旧的元素。
|
||||
* 返回 `false`。
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
public boolean containsNearbyDuplicate(int[] nums, int k) {
|
||||
Set<Integer> set = new HashSet<>();
|
||||
for (int i = 0; i < nums.length; ++i) {
|
||||
if (set.contains(nums[i])) return true;
|
||||
set.add(nums[i]);
|
||||
if (set.size() > k) {
|
||||
set.remove(nums[i - k]);
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
* 时间复杂度:$O(n)$
|
||||
我们会做 $n$ 次 `搜索`,`删除`,`插入` 操作,每次操作都耗费常数时间。
|
||||
|
||||
* 空间复杂度:$O(\min(n, k))$
|
||||
开辟的额外空间取决于散列表中存储的元素的个数,也就是滑动窗口的大小 $O(\min(n,k))$。
|
||||
|
||||
@ -0,0 +1,53 @@
|
||||
### 解题思路
|
||||
|
||||
[参考大佬解法](https://leetcode.com/problems/largest-palindrome-product/discuss/276101/Python3-Math-and-Non-math-solutions-with-detailed-explanation)
|
||||
方法一 迭代+剪枝
|
||||
|
||||
### 代码
|
||||
|
||||
* python3
|
||||
|
||||
```python3
|
||||
# 1迭代法
|
||||
class Solution:
|
||||
def largestPalindrome(self, n: int) -> int:
|
||||
if n == 1: return 9
|
||||
hi = 10 ** n - 1 # 最大的n位数
|
||||
lo = 10 ** (n - 1) # 最小的n位数
|
||||
maxfirst = (hi ** 2) // (10 ** n) # 前半部分最大值
|
||||
for first in range(maxfirst, lo - 1, -1):
|
||||
palidrome = int(str(first) + str(first)[::-1])
|
||||
# 因为长度为偶数的palidrom一定能被11整除,所以我们假设其中一个的因数能被11整除,即可以进行11的步长搜索结果
|
||||
x = hi // 11 * 11 # 从高往低搜索
|
||||
for factor in range(x, lo - 1, -11):
|
||||
if palidrome % factor == 0 and lo <= palidrome // factor <= hi:d
|
||||
return palidrome % 1337
|
||||
if palidrome // factor > hi:
|
||||
break
|
||||
```
|
||||
|
||||
方法二 数学法
|
||||
设因数为`X,Y`,令$X,Y=10^{n}-i,10^{n}-j$,此时`i>=1,j>=1`; 设`a=i+j`; 设回文序列为`p`,并令$p=X*Y=upper*10^{n}+lower\\$
|
||||
->又$p=X*Y=10^{n}*10^{n}-10^{n}*j-10^{n}*i+i*j=(10^{n}-i-j)*10^{n}+i*j=(10^n-a)*10^n+lower$,此时$upper=10^{n}-a,lower=i*j=i*(a-i)\\$
|
||||
->则$(i-a/2)^{2}=0.25*a^{2}-lower\\$
|
||||
又因为`i,j`均为整数,那么`2*i-a`也一定为整数,所以$\sqrt{a^{2}-4*lower}$一定为整数,那么从`a>=2`开始,找到以`upper`为前半部分,`lower`为后半部分的回文序列,再筛选符合$\sqrt{a^{2}-4*lower}$为整数的`lower`和`a`
|
||||
|
||||
* python3
|
||||
|
||||
```python3
|
||||
# 2数学法
|
||||
class Solution:
|
||||
def largestPalindrome(self, n: int) -> int:
|
||||
if n == 1: return 9
|
||||
a = 2
|
||||
hi = 10 ** n - 1
|
||||
lo = 10 ** (n - 1)
|
||||
while a < 2 * 10 ** n:
|
||||
upper = 10 ** n - a
|
||||
lower = int(str(upper)[::-1])
|
||||
if a ** 2 - 4 * lower >= 0 and (a ** 2 - 4 * lower) ** 0.5 == int((a ** 2 - 4 * lower)**0.5):
|
||||
num = int(str(upper)+ str(upper)[::-1])
|
||||
return num % 1337
|
||||
a += 1
|
||||
```
|
||||
|
||||
@ -0,0 +1,90 @@
|
||||
#### 方法一:贪心
|
||||
|
||||
**分析**
|
||||
|
||||
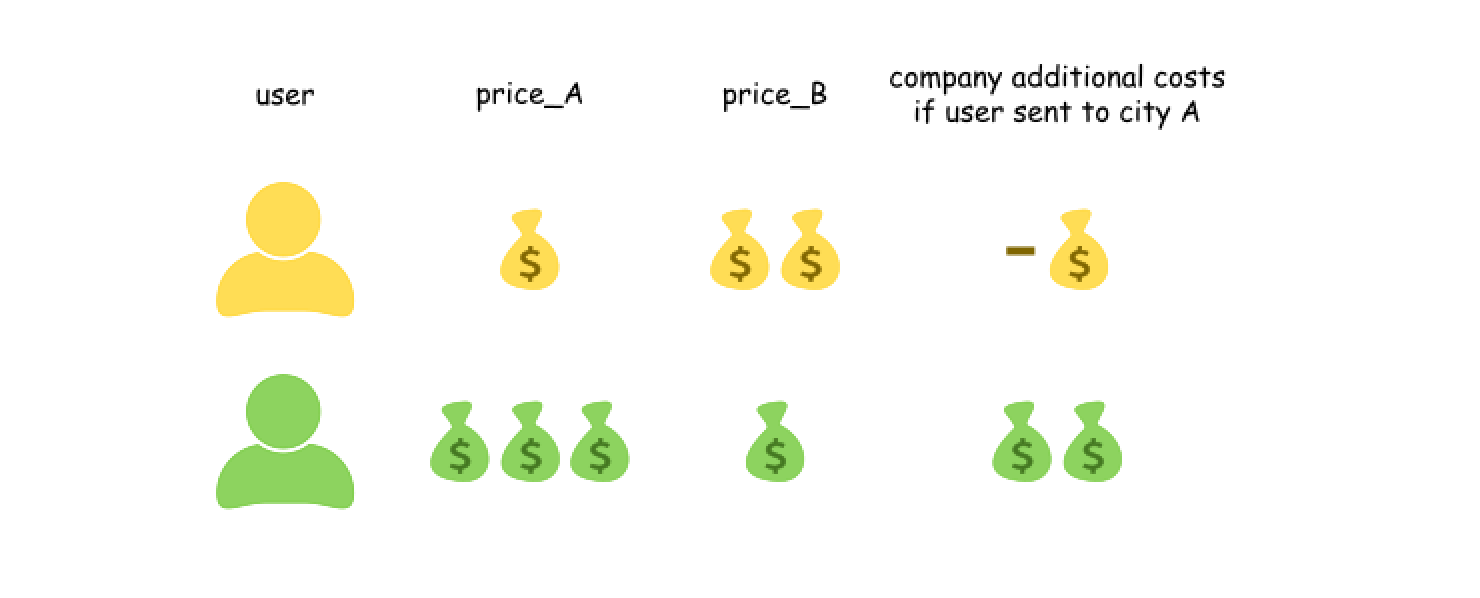
我们这样来看这个问题,公司首先将这 $2N$ 个人全都安排飞往 $B$ 市,再选出 $N$ 个人改变它们的行程,让他们飞往 $A$ 市。如果选择改变一个人的行程,那么公司将会额外付出 `price_A - price_B` 的费用,这个费用可正可负。
|
||||
|
||||
|
||||
|
||||
因此最优的方案是,选出 `price_A - price_B` 最小的 $N$ 个人,让他们飞往 `A` 市,其余人飞往 `B` 市。
|
||||
|
||||
**算法**
|
||||
|
||||
- 按照 `price_A - price_B` 从小到大排序;
|
||||
|
||||
- 将前 $N$ 个人飞往 `A` 市,其余人飞往 `B` 市,并计算出总费用。
|
||||
|
||||
* [sol1]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def twoCitySchedCost(self, costs: List[List[int]]) -> int:
|
||||
# Sort by a gain which company has
|
||||
# by sending a person to city A and not to city B
|
||||
costs.sort(key = lambda x : x[0] - x[1])
|
||||
|
||||
total = 0
|
||||
n = len(costs) // 2
|
||||
# To optimize the company expenses,
|
||||
# send the first n persons to the city A
|
||||
# and the others to the city B
|
||||
for i in range(n):
|
||||
total += costs[i][0] + costs[i + n][1]
|
||||
return total
|
||||
```
|
||||
|
||||
* [sol1]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int twoCitySchedCost(int[][] costs) {
|
||||
// Sort by a gain which company has
|
||||
// by sending a person to city A and not to city B
|
||||
Arrays.sort(costs, new Comparator<int[]>() {
|
||||
@Override
|
||||
public int compare(int[] o1, int[] o2) {
|
||||
return o1[0] - o1[1] - (o2[0] - o2[1]);
|
||||
}
|
||||
});
|
||||
|
||||
int total = 0;
|
||||
int n = costs.length / 2;
|
||||
// To optimize the company expenses,
|
||||
// send the first n persons to the city A
|
||||
// and the others to the city B
|
||||
for (int i = 0; i < n; ++i) total += costs[i][0] + costs[i + n][1];
|
||||
return total;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int twoCitySchedCost(vector<vector<int>>& costs) {
|
||||
// Sort by a gain which company has
|
||||
// by sending a person to city A and not to city B
|
||||
sort(begin(costs), end(costs),
|
||||
[](const vector<int> &o1, const vector<int> &o2) {
|
||||
return (o1[0] - o1[1] < o2[0] - o2[1]);
|
||||
});
|
||||
|
||||
int total = 0;
|
||||
int n = costs.size() / 2;
|
||||
// To optimize the company expenses,
|
||||
// send the first n persons to the city A
|
||||
// and the others to the city B
|
||||
for (int i = 0; i < n; ++i) total += costs[i][0] + costs[i + n][1];
|
||||
return total;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
* 时间复杂度:$O(N \log N)$,需要对 `price_A - price_B` 进行排序。
|
||||
|
||||
* 空间复杂度:$O(1)$。
|
||||
|
||||
@ -0,0 +1,393 @@
|
||||
#### 方法一:两次遍历
|
||||
|
||||
**思路及解法**
|
||||
|
||||
我们可以将「相邻的孩子中,评分高的孩子必须获得更多的糖果」这句话拆分为两个规则,分别处理。
|
||||
|
||||
- 左规则:当 $\textit{ratings}[i - 1] < \textit{ratings}[i]$ 时,$i$ 号学生的糖果数量将比 $i - 1$ 号孩子的糖果数量多。
|
||||
|
||||
- 右规则:当 $\textit{ratings}[i] > \textit{ratings}[i + 1]$ 时,$i$ 号学生的糖果数量将比 $i + 1$ 号孩子的糖果数量多。
|
||||
|
||||
我们遍历该数组两次,处理出每一个学生分别满足左规则或右规则时,最少需要被分得的糖果数量。每个人最终分得的糖果数量即为这两个数量的最大值。
|
||||
|
||||
具体地,以左规则为例:我们从左到右遍历该数组,假设当前遍历到位置 $i$,如果有 $\textit{ratings}[i - 1] < \textit{ratings}[i]$ 那么 $i$ 号学生的糖果数量将比 $i - 1$ 号孩子的糖果数量多,我们令 $\textit{left}[i] = \textit{left}[i - 1] + 1$ 即可,否则我们令 $\textit{left}[i] = 1$。
|
||||
|
||||
在实际代码中,我们先计算出左规则 $\textit{left}$ 数组,在计算右规则的时候只需要用单个变量记录当前位置的右规则,同时计算答案即可。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int candy(vector<int>& ratings) {
|
||||
int n = ratings.size();
|
||||
vector<int> left(n);
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (i > 0 && ratings[i] > ratings[i - 1]) {
|
||||
left[i] = left[i - 1] + 1;
|
||||
} else {
|
||||
left[i] = 1;
|
||||
}
|
||||
}
|
||||
int right = 0, ret = 0;
|
||||
for (int i = n - 1; i >= 0; i--) {
|
||||
if (i < n - 1 && ratings[i] > ratings[i + 1]) {
|
||||
right++;
|
||||
} else {
|
||||
right = 1;
|
||||
}
|
||||
ret += max(left[i], right);
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int candy(int[] ratings) {
|
||||
int n = ratings.length;
|
||||
int[] left = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (i > 0 && ratings[i] > ratings[i - 1]) {
|
||||
left[i] = left[i - 1] + 1;
|
||||
} else {
|
||||
left[i] = 1;
|
||||
}
|
||||
}
|
||||
int right = 0, ret = 0;
|
||||
for (int i = n - 1; i >= 0; i--) {
|
||||
if (i < n - 1 && ratings[i] > ratings[i + 1]) {
|
||||
right++;
|
||||
} else {
|
||||
right = 1;
|
||||
}
|
||||
ret += Math.max(left[i], right);
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func candy(ratings []int) (ans int) {
|
||||
n := len(ratings)
|
||||
left := make([]int, n)
|
||||
for i, r := range ratings {
|
||||
if i > 0 && r > ratings[i-1] {
|
||||
left[i] = left[i-1] + 1
|
||||
} else {
|
||||
left[i] = 1
|
||||
}
|
||||
}
|
||||
right := 0
|
||||
for i := n - 1; i >= 0; i-- {
|
||||
if i < n-1 && ratings[i] > ratings[i+1] {
|
||||
right++
|
||||
} else {
|
||||
right = 1
|
||||
}
|
||||
ans += max(left[i], right)
|
||||
}
|
||||
return
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def candy(self, ratings: List[int]) -> int:
|
||||
n = len(ratings)
|
||||
left = [0] * n
|
||||
for i in range(n):
|
||||
if i > 0 and ratings[i] > ratings[i - 1]:
|
||||
left[i] = left[i - 1] + 1
|
||||
else:
|
||||
left[i] = 1
|
||||
|
||||
right = ret = 0
|
||||
for i in range(n - 1, -1, -1):
|
||||
if i < n - 1 and ratings[i] > ratings[i + 1]:
|
||||
right += 1
|
||||
else:
|
||||
right = 1
|
||||
ret += max(left[i], right)
|
||||
|
||||
return ret
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var candy = function(ratings) {
|
||||
const n = ratings.length;
|
||||
const left = new Array(n).fill(0);
|
||||
for (let i = 0; i < n; i++) {
|
||||
if (i > 0 && ratings[i] > ratings[i - 1]) {
|
||||
left[i] = left[i - 1] + 1;
|
||||
} else {
|
||||
left[i] = 1;
|
||||
}
|
||||
}
|
||||
|
||||
let right = 0, ret = 0;
|
||||
for (let i = n - 1; i > -1; i--) {
|
||||
if (i < n - 1 && ratings[i] > ratings[i + 1]) {
|
||||
right++;
|
||||
} else {
|
||||
right = 1;
|
||||
}
|
||||
ret += Math.max(left[i], right);
|
||||
}
|
||||
return ret;
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
int candy(int* ratings, int ratingsSize) {
|
||||
int left[ratingsSize];
|
||||
for (int i = 0; i < ratingsSize; i++) {
|
||||
if (i > 0 && ratings[i] > ratings[i - 1]) {
|
||||
left[i] = left[i - 1] + 1;
|
||||
} else {
|
||||
left[i] = 1;
|
||||
}
|
||||
}
|
||||
int right = 0, ret = 0;
|
||||
for (int i = ratingsSize - 1; i >= 0; i--) {
|
||||
if (i < ratingsSize - 1 && ratings[i] > ratings[i + 1]) {
|
||||
right++;
|
||||
} else {
|
||||
right = 1;
|
||||
}
|
||||
ret += fmax(left[i], right);
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n)$,其中 $n$ 是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。
|
||||
|
||||
- 空间复杂度:$O(n)$,其中 $n$ 是孩子的数量。我们需要保存所有的左规则对应的糖果数量。
|
||||
|
||||
#### 方法二:常数空间遍历
|
||||
|
||||
**思路及解法**
|
||||
|
||||
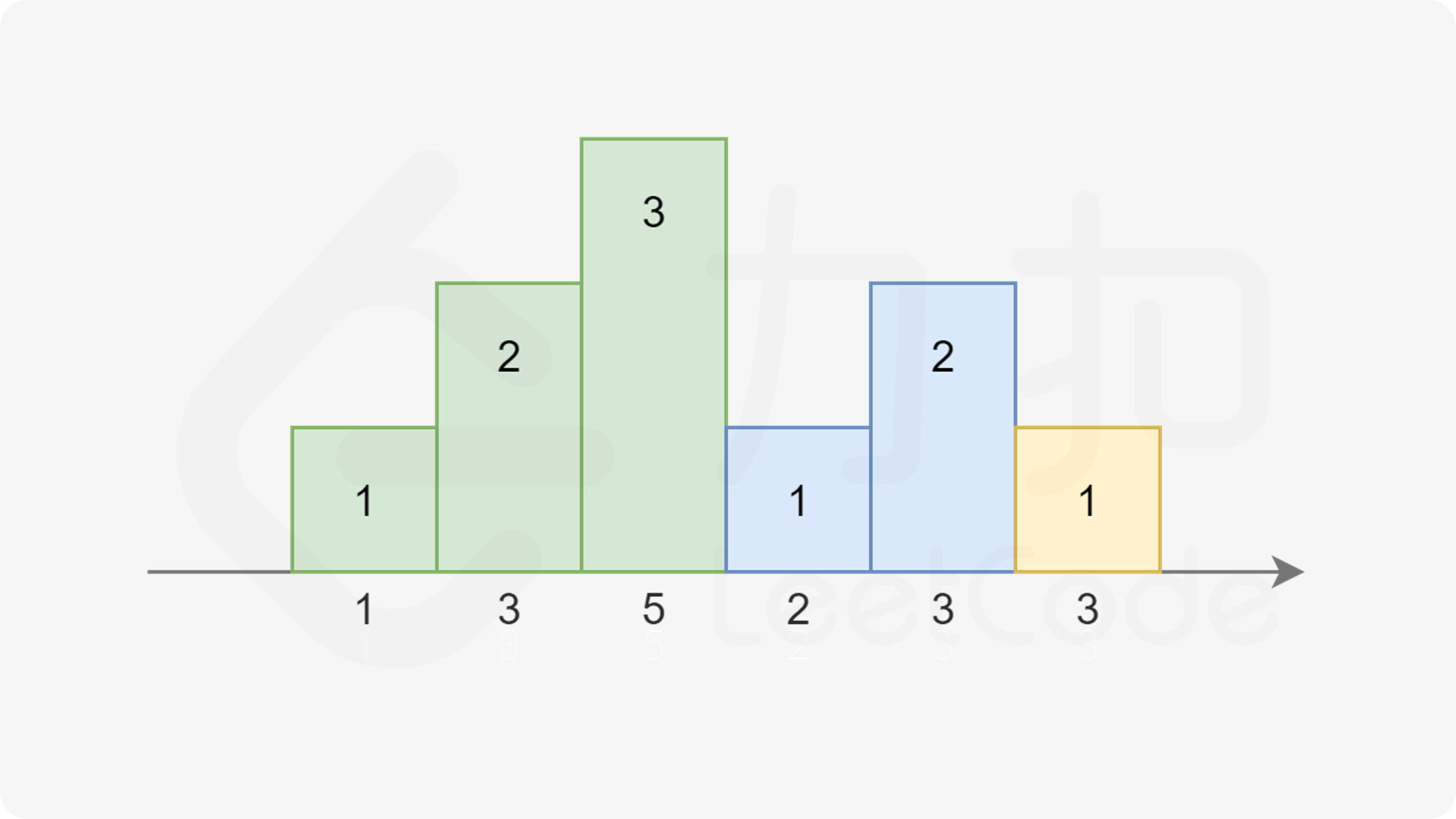
注意到糖果总是尽量少给,且从 $1$ 开始累计,每次要么比相邻的同学多给一个,要么重新置为 $1$。依据此规则,我们可以画出下图:
|
||||
|
||||
|
||||
|
||||
其中相同颜色的柱状图的高度总恰好为 $1,2,3 \dots$。
|
||||
|
||||
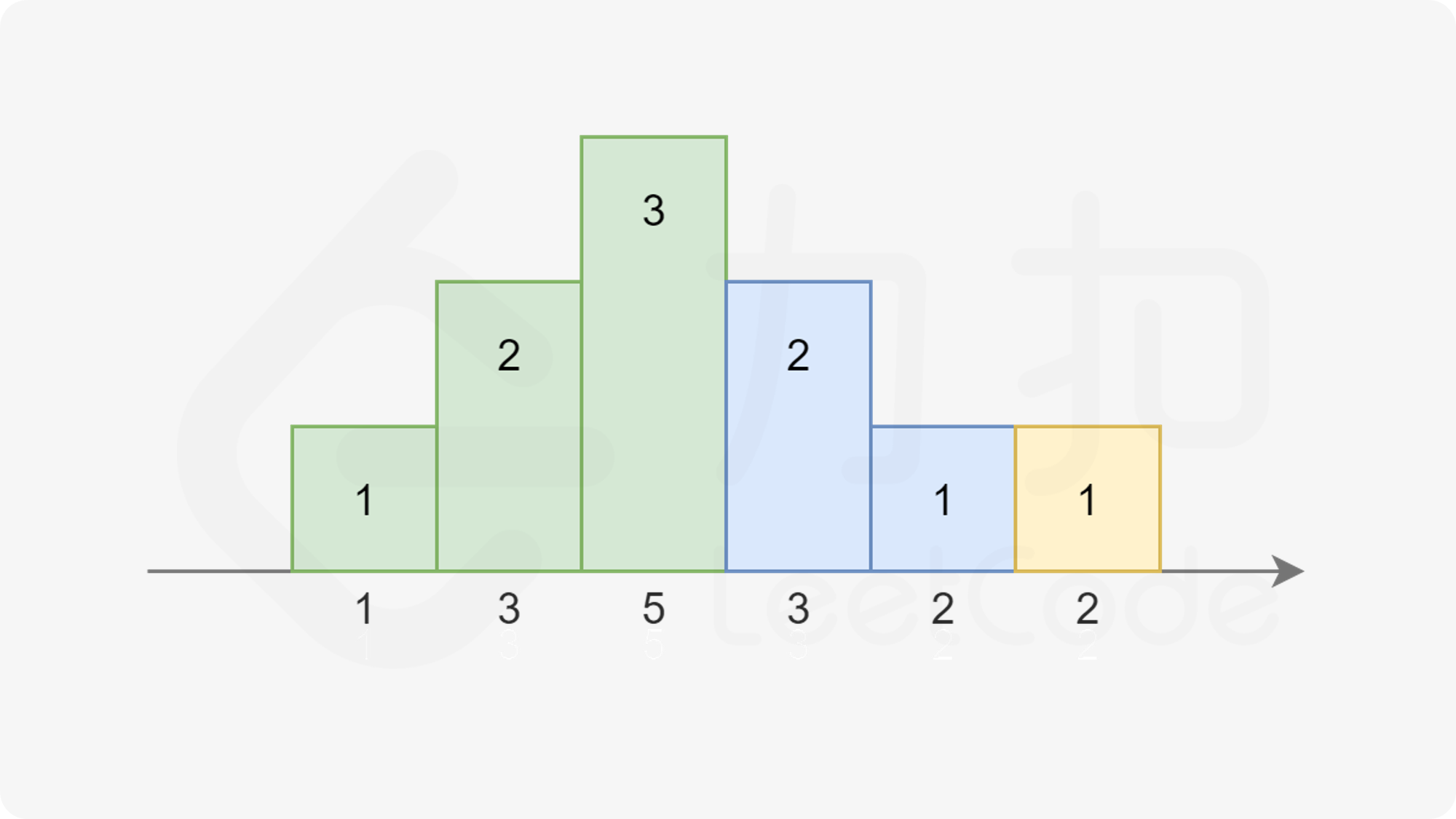
而高度也不一定一定是升序,也可能是 $\dots 3,2,1$ 的降序:
|
||||
|
||||
|
||||
|
||||
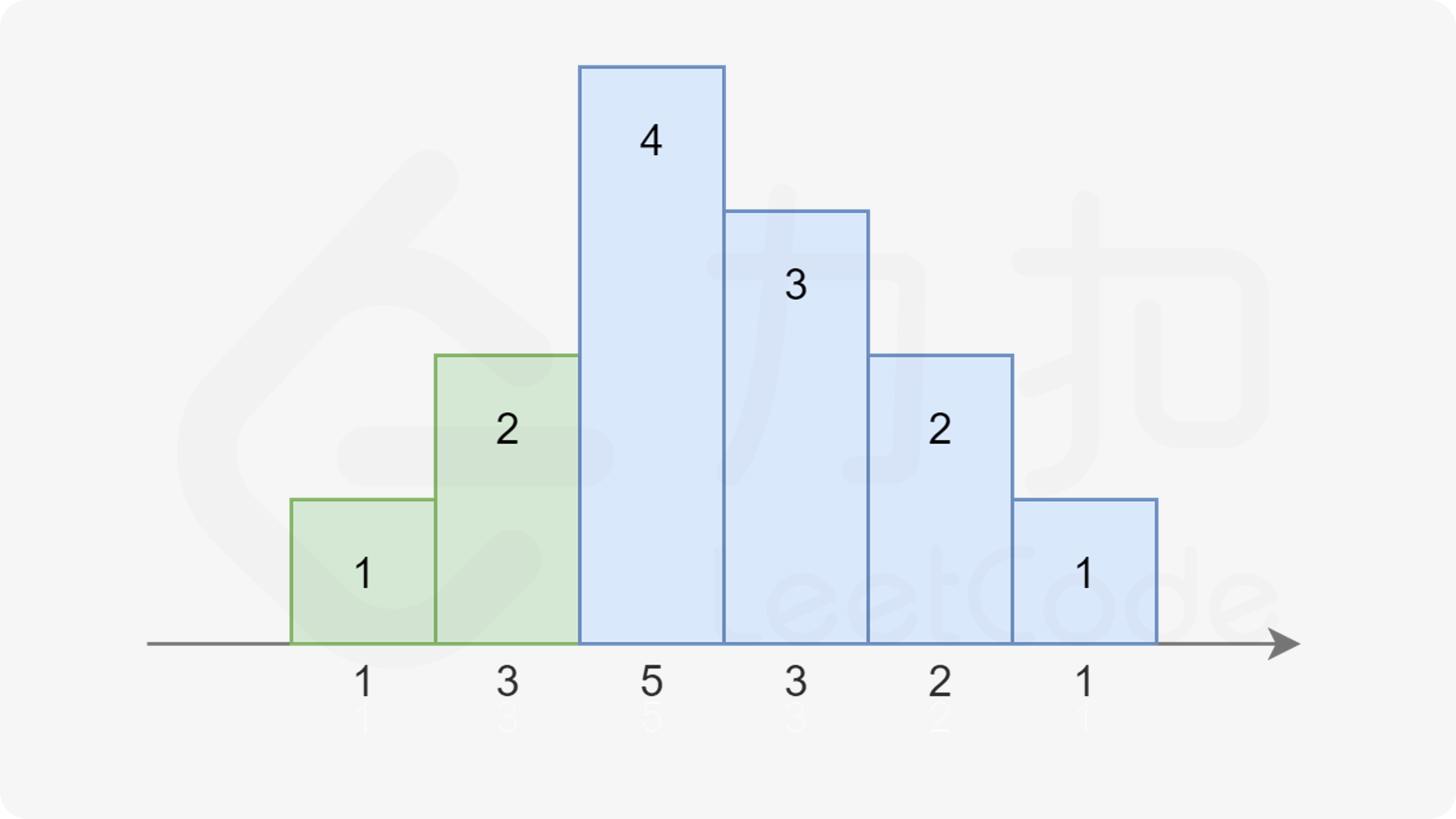
注意到在上图中,对于第三个同学,他既可以被认为是属于绿色的升序部分,也可以被认为是属于蓝色的降序部分。因为他同时比两边的同学评分更高。我们对序列稍作修改:
|
||||
|
||||
|
||||
|
||||
注意到右边的升序部分变长了,使得第三个同学不得不被分配 $4$ 个糖果。
|
||||
|
||||
依据前面总结的规律,我们可以提出本题的解法。我们从左到右枚举每一个同学,记前一个同学分得的糖果数量为 $\textit{pre}$:
|
||||
|
||||
- 如果当前同学比上一个同学评分高,说明我们就在最近的递增序列中,直接分配给该同学 $\textit{pre} + 1$ 个糖果即可。
|
||||
|
||||
- 否则我们就在一个递减序列中,我们直接分配给当前同学一个糖果,并把该同学所在的递减序列中所有的同学都再多分配一个糖果,以保证糖果数量还是满足条件。
|
||||
- 我们无需显式地额外分配糖果,只需要记录当前的递减序列长度,即可知道需要额外分配的糖果数量。
|
||||
|
||||
- 同时注意当当前的递减序列长度和上一个递增序列等长时,需要把最近的递增序列的最后一个同学也并进递减序列中。
|
||||
|
||||
这样,我们只要记录当前递减序列的长度 $\textit{dec}$,最近的递增序列的长度 $\textit{inc}$ 和前一个同学分得的糖果数量 $\textit{pre}$ 即可。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol2-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int candy(vector<int>& ratings) {
|
||||
int n = ratings.size();
|
||||
int ret = 1;
|
||||
int inc = 1, dec = 0, pre = 1;
|
||||
for (int i = 1; i < n; i++) {
|
||||
if (ratings[i] >= ratings[i - 1]) {
|
||||
dec = 0;
|
||||
pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;
|
||||
ret += pre;
|
||||
inc = pre;
|
||||
} else {
|
||||
dec++;
|
||||
if (dec == inc) {
|
||||
dec++;
|
||||
}
|
||||
ret += dec;
|
||||
pre = 1;
|
||||
}
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int candy(int[] ratings) {
|
||||
int n = ratings.length;
|
||||
int ret = 1;
|
||||
int inc = 1, dec = 0, pre = 1;
|
||||
for (int i = 1; i < n; i++) {
|
||||
if (ratings[i] >= ratings[i - 1]) {
|
||||
dec = 0;
|
||||
pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;
|
||||
ret += pre;
|
||||
inc = pre;
|
||||
} else {
|
||||
dec++;
|
||||
if (dec == inc) {
|
||||
dec++;
|
||||
}
|
||||
ret += dec;
|
||||
pre = 1;
|
||||
}
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Golang]
|
||||
|
||||
```go
|
||||
func candy(ratings []int) int {
|
||||
n := len(ratings)
|
||||
ans, inc, dec, pre := 1, 1, 0, 1
|
||||
for i := 1; i < n; i++ {
|
||||
if ratings[i] >= ratings[i-1] {
|
||||
dec = 0
|
||||
if ratings[i] == ratings[i-1] {
|
||||
pre = 1
|
||||
} else {
|
||||
pre++
|
||||
}
|
||||
ans += pre
|
||||
inc = pre
|
||||
} else {
|
||||
dec++
|
||||
if dec == inc {
|
||||
dec++
|
||||
}
|
||||
ans += dec
|
||||
pre = 1
|
||||
}
|
||||
}
|
||||
return ans
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def candy(self, ratings: List[int]) -> int:
|
||||
n = len(ratings)
|
||||
ret = 1
|
||||
inc, dec, pre = 1, 0, 1
|
||||
|
||||
for i in range(1, n):
|
||||
if ratings[i] >= ratings[i - 1]:
|
||||
dec = 0
|
||||
pre = (1 if ratings[i] == ratings[i - 1] else pre + 1)
|
||||
ret += pre
|
||||
inc = pre
|
||||
else:
|
||||
dec += 1
|
||||
if dec == inc:
|
||||
dec += 1
|
||||
ret += dec
|
||||
pre = 1
|
||||
|
||||
return ret
|
||||
```
|
||||
|
||||
* [sol2-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var candy = function(ratings) {
|
||||
const n = ratings.length;
|
||||
let ret = 1;
|
||||
let inc = 1, dec = 0, pre = 1;
|
||||
|
||||
for (let i = 1; i < n; i++) {
|
||||
if (ratings[i] >= ratings[i - 1]) {
|
||||
dec = 0;
|
||||
if (ratings[i] === ratings[i - 1]) pre = 1;
|
||||
else pre++;
|
||||
ret += pre;
|
||||
inc = pre;
|
||||
} else {
|
||||
dec++;
|
||||
if (dec === inc) {
|
||||
dec++;
|
||||
}
|
||||
ret += dec;
|
||||
pre = 1;
|
||||
}
|
||||
}
|
||||
return ret;
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-C]
|
||||
|
||||
```C
|
||||
int candy(int* ratings, int ratingsSize) {
|
||||
int ret = 1;
|
||||
int inc = 1, dec = 0, pre = 1;
|
||||
for (int i = 1; i < ratingsSize; i++) {
|
||||
if (ratings[i] >= ratings[i - 1]) {
|
||||
dec = 0;
|
||||
pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;
|
||||
ret += pre;
|
||||
inc = pre;
|
||||
} else {
|
||||
dec++;
|
||||
if (dec == inc) {
|
||||
dec++;
|
||||
}
|
||||
ret += dec;
|
||||
pre = 1;
|
||||
}
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n)$,其中 $n$ 是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。
|
||||
|
||||
- 空间复杂度:$O(1)$。我们只需要常数的空间保存若干变量。
|
||||
|
||||
@ -0,0 +1,233 @@
|
||||
## 二分
|
||||
|
||||
往常我们使用「二分」进行查值,需要确保序列本身满足「二段性」:当选定一个端点(基准值)后,结合「一段满足 & 另一段不满足」的特性来实现“折半”的查找效果。
|
||||
|
||||
但本题求的是峰顶索引值,如果我们选定数组头部或者尾部元素,其实无法根据大小关系“直接”将数组分成两段。
|
||||
|
||||
但可以利用题目发现如下性质:**由于 `arr` 数值各不相同,因此峰顶元素左侧必然满足严格单调递增,峰顶元素右侧必然不满足。**
|
||||
|
||||
因此 **以峰顶元素为分割点的 `arr` 数组,根据与 前一元素/后一元素 的大小关系,具有二段性:**
|
||||
|
||||
* 峰顶元素左侧满足 $arr[i-1] < arr[i]$ 性质,右侧不满足
|
||||
* 峰顶元素右侧满足 $arr[i] > arr[i+1]$ 性质,左侧不满足
|
||||
|
||||
因此我们可以选择任意条件,写出若干「二分」版本。
|
||||
|
||||
代码:
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
// 根据 arr[i-1] < arr[i] 在 [1,n-1] 范围内找值
|
||||
// 峰顶元素为符合条件的最靠近中心的元素
|
||||
public int peakIndexInMountainArray(int[] arr) {
|
||||
int n = arr.length;
|
||||
int l = 1, r = n - 1;
|
||||
while (l < r) {
|
||||
int mid = l + r + 1 >> 1;
|
||||
if (arr[mid - 1] < arr[mid]) l = mid;
|
||||
else r = mid - 1;
|
||||
}
|
||||
return r;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
// 根据 arr[i] > arr[i+1] 在 [0,n-2] 范围内找值
|
||||
// 峰顶元素为符合条件的最靠近中心的元素值
|
||||
public int peakIndexInMountainArray(int[] arr) {
|
||||
int n = arr.length;
|
||||
int l = 0, r = n - 2;
|
||||
while (l < r) {
|
||||
int mid = l + r >> 1;
|
||||
if (arr[mid] > arr[mid + 1]) r = mid;
|
||||
else l = mid + 1;
|
||||
}
|
||||
return r;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
// 根据 arr[i-1] > arr[i] 在 [1,n-1] 范围内找值
|
||||
// 峰顶元素为符合条件的最靠近中心的元素的前一个值
|
||||
public int peakIndexInMountainArray(int[] arr) {
|
||||
int n = arr.length;
|
||||
int l = 1, r = n - 1;
|
||||
while (l < r) {
|
||||
int mid = l + r >> 1;
|
||||
if (arr[mid - 1] > arr[mid]) r = mid;
|
||||
else l = mid + 1;
|
||||
}
|
||||
return r - 1;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
// 根据 arr[i] < arr[i+1] 在 [0,n-2] 范围内找值
|
||||
// 峰顶元素为符合条件的最靠近中心的元素的下一个值
|
||||
public int peakIndexInMountainArray(int[] arr) {
|
||||
int n = arr.length;
|
||||
int l = 0, r = n - 2;
|
||||
while (l < r) {
|
||||
int mid = l + r + 1 >> 1;
|
||||
if (arr[mid] < arr[mid + 1]) l = mid;
|
||||
else r = mid - 1;
|
||||
}
|
||||
return r + 1;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(\log{n})$
|
||||
* 空间复杂度:$O(1)$
|
||||
|
||||
---
|
||||
|
||||
## 三分
|
||||
|
||||
事实上,我们还可以利用「三分」来解决这个问题。
|
||||
|
||||
顾名思义,**「三分」就是使用两个端点将区间分成三份,然后通过每次否决三分之一的区间来逼近目标值。**
|
||||
|
||||
具体的,由于峰顶元素为全局最大值,因此我们可以每次将当前区间分为 $[l, m1]$、$[m1, m2]$ 和 $[m2, r]$ 三段,如果满足 $arr[m1] > arr[m2]$,说明峰顶元素不可能存在与 $[m2, r]$ 中,让 $r = m2 - 1$ 即可。另外一个区间分析同理。
|
||||
|
||||
代码:
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int peakIndexInMountainArray(int[] arr) {
|
||||
int n = arr.length;
|
||||
int l = 0, r = n - 1;
|
||||
while (l < r) {
|
||||
int m1 = l + (r - l) / 3;
|
||||
int m2 = r - (r - l) / 3;
|
||||
if (arr[m1] > arr[m2]) r = m2 - 1;
|
||||
else l = m1 + 1;
|
||||
}
|
||||
return r;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(\log{n})$
|
||||
* 空间复杂度:$O(1)$
|
||||
|
||||
---
|
||||
|
||||
## 二分 & 三分 & k 分 ?
|
||||
|
||||
必须说明一点,「二分」和「三分」在渐进复杂度上都是一样的,都可以通过换底公式转化为可忽略的常数,因此两者的复杂度都是 $O(\log{n})$。
|
||||
|
||||
因此选择「二分」还是「三分」取决于要解决的是什么问题:
|
||||
|
||||
* 二分通常用来解决单调函数的找 $target$ 问题,但进一步深入我们发现只需要满足「二段性」就能使用「二分」来找分割点;
|
||||
* 三分则是解决单峰函数极值问题。
|
||||
|
||||
**因此一般我们将「通过比较两个端点,每次否决 1/3 区间 来解决单峰最值问题」的做法称为「三分」;而不是简单根据单次循环内将区间分为多少份来判定是否为「三分」。**
|
||||
|
||||
随手写了一段反例代码:
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int peakIndexInMountainArray(int[] arr) {
|
||||
int left = 0, right = arr.length - 1;
|
||||
while(left < right) {
|
||||
int m1 = left + (right - left) / 3;
|
||||
int m2 = right - (right - left + 2) / 3;
|
||||
if (arr[m1] > arr[m1 + 1]) {
|
||||
right = m1;
|
||||
} else if (arr[m2] < arr[m2 + 1]) {
|
||||
left = m2 + 1;
|
||||
} else {
|
||||
left = m1;
|
||||
right = m2;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这并不是「三分」做法,最多称为「变形二分」。本质还是利用「二段性」来做分割的,只不过同时 check 了两个端点而已。
|
||||
|
||||
如果这算「三分」的话,那么我能在一次循环里面划分 $k - 1$ 个端点来实现 $k$ 分?
|
||||
|
||||
**显然这是没有意义的,因为按照这种思路写出来的所谓的「四分」、「五分」、「k 分」是需要增加同等数量的分支判断的。这时候单次 `while` 决策就不能算作 $O(1)$ 了,而是需要在 $O(k)$ 的复杂度内决定在哪个分支,就跟上述代码有三个分支进行判断一样。** 因此,这种写法只能算作是「变形二分」。
|
||||
|
||||
**综上,只有「二分」和「三分」的概念,不存在所谓的 $k$ 分。** 同时题解中的「三分」部分提供的做法就是标准的「三分」做法。
|
||||
|
||||
---
|
||||
|
||||
## 进阶
|
||||
|
||||
更进一步的,如果存在多个峰值,返回任意一个的话,是否还可以二分?为什么?
|
||||
|
||||
[(原题)162. 寻找峰值](https://leetcode-cn.com/problems/find-peak-element/) : [(题解)关于能够「二分」的两点证明](https://leetcode-cn.com/problems/find-peak-element/solution/gong-shui-san-xie-noxiang-xin-ke-xue-xi-qva7v/)
|
||||
|
||||
---
|
||||
|
||||
## 其他「二分」内容
|
||||
|
||||
题目简单?考虑加餐一道 [01 背包变形题](https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247488868&idx=1&sn=5e54a1d091a8249d3033a28fc299076d&chksm=fd9cbe7bcaeb376d1ee8a753ebc57358e5605fc1a3b51865eb0f758fb3e6e4688e1b0acfa902&token=730964724&lang=zh_CN#rd)。
|
||||
|
||||
或是考虑加练如下「二分」题目 🍭🍭
|
||||
|
||||
| 题目 | 题解 | 难度 | 推荐指数 |
|
||||
| --------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------ | ---- | -------- |
|
||||
| [4. 寻找两个正序数组的中位数](https://leetcode-cn.com/problems/median-of-two-sorted-arrays/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/shua-chuan-lc-po-su-jie-fa-fen-zhi-jie-f-wtu2/) | 困难 | 🤩🤩🤩🤩 |
|
||||
| [29. 两数相除](https://leetcode-cn.com/problems/divide-two-integers/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/divide-two-integers/solution/shua-chuan-lc-er-fen-bei-zeng-cheng-fa-j-m73b) | 中等 | 🤩🤩🤩 |
|
||||
| [33. 搜索旋转排序数组](https://leetcode-cn.com/problems/search-in-rotated-sorted-array/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/search-in-rotated-sorted-array/solution/shua-chuan-lc-yan-ge-ologn100yi-qi-kan-q-xifo/) | 中等 | 🤩🤩🤩🤩🤩 |
|
||||
| [34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/solution/sha-sha-gao-bu-qing-ru-he-ding-yi-er-fen-rrj1/) | 中等 | 🤩🤩🤩🤩🤩 |
|
||||
| [35. 搜索插入位置](https://leetcode-cn.com/problems/search-insert-position/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/search-insert-position/solution/shua-chuan-lc-jian-dan-mo-ni-ti-by-ac_oi-7d5t/) | 简单 | 🤩🤩🤩🤩🤩 |
|
||||
| [74. 搜索二维矩阵](https://leetcode-cn.com/problems/search-a-2d-matrix/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/search-a-2d-matrix/solution/gong-shui-san-xie-yi-ti-shuang-jie-er-fe-l0pq/) | 中等 | 🤩🤩🤩🤩 |
|
||||
| [81. 搜索旋转排序数组 II](https://leetcode-cn.com/problems/search-in-rotated-sorted-array-ii/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/search-in-rotated-sorted-array-ii/solution/gong-shui-san-xie-xiang-jie-wei-he-yuan-xtam4//) | 中等 | 🤩🤩🤩🤩 |
|
||||
| [153. 寻找旋转排序数组中的最小值](https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/solution/gong-shui-san-xie-yan-ge-olognyi-qi-kan-6d969/) | 中等 | 🤩🤩🤩 |
|
||||
| [154. 寻找旋转排序数组中的最小值 II](https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/solution/gong-shui-san-xie-xiang-jie-wei-he-yuan-7xbty/) | 困难 | 🤩🤩🤩 |
|
||||
| [162. 寻找峰值](https://leetcode-cn.com/problems/find-peak-element/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/find-peak-element/solution/gong-shui-san-xie-noxiang-xin-ke-xue-xi-qva7v/) | 中等 | 🤩🤩🤩🤩🤩 |
|
||||
| [220. 存在重复元素 III](https://leetcode-cn.com/problems/contains-duplicate-iii/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/contains-duplicate-iii/solution/gong-shui-san-xie-yi-ti-shuang-jie-hua-d-dlnv/) | 中等 | 🤩🤩🤩 |
|
||||
| [274. H 指数](https://leetcode-cn.com/problems/h-index/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/h-index/solution/gong-shui-san-xie-li-yong-er-duan-xing-z-1jxw/) | 中等 | 🤩🤩🤩 |
|
||||
| [275. H 指数 II](https://leetcode-cn.com/problems/h-index-ii/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/h-index-ii/solution/gong-shui-san-xie-liang-chong-er-fen-ji-sovjb/) | 中等 | 🤩🤩🤩 |
|
||||
| [278. 第一个错误的版本](https://leetcode-cn.com/problems/first-bad-version/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/first-bad-version/solution/gong-shui-san-xie-shi-yong-jiao-hu-han-s-8hpv/) | 简单 | 🤩🤩🤩🤩 |
|
||||
| [352. 将数据流变为多个不相交区间](https://leetcode-cn.com/problems/data-stream-as-disjoint-intervals/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/data-stream-as-disjoint-intervals/solution/gong-shui-san-xie-yi-ti-shuang-jie-er-fe-afrk/) | 困难 | 🤩🤩🤩🤩 |
|
||||
| [354. 俄罗斯套娃信封问题](https://leetcode-cn.com/problems/russian-doll-envelopes/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/russian-doll-envelopes/solution/zui-chang-shang-sheng-zi-xu-lie-bian-xin-6s8d/) | 困难 | 🤩🤩🤩 |
|
||||
| [363. 矩形区域不超过 K 的最大数值和](https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/solution/gong-shui-san-xie-you-hua-mei-ju-de-ji-b-dh8s/) | 困难 | 🤩🤩🤩 |
|
||||
| [374. 猜数字大小](https://leetcode-cn.com/problems/guess-number-higher-or-lower/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/guess-number-higher-or-lower/solution/gong-shui-san-xie-shi-yong-jiao-hu-han-s-tocm/) | 简单 | 🤩🤩🤩 |
|
||||
| [441. 排列硬币](https://leetcode-cn.com/problems/arranging-coins/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/arranging-coins/solution/gong-shui-san-xie-yi-ti-shuang-jie-shu-x-sv9o/) | 简单 | 🤩🤩🤩 |
|
||||
| [528. 按权重随机选择](https://leetcode-cn.com/problems/random-pick-with-weight/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/random-pick-with-weight/solution/gong-shui-san-xie-yi-ti-shuang-jie-qian-8bx50/) | 中等 | 🤩🤩🤩🤩 |
|
||||
| [611. 有效三角形的个数](https://leetcode-cn.com/problems/valid-triangle-number/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/valid-triangle-number/solution/gong-shui-san-xie-yi-ti-san-jie-jian-dan-y1we/) | 中等 | 🤩🤩🤩🤩 |
|
||||
| [704. 二分查找](https://leetcode-cn.com/problems/binary-search/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/binary-search/solution/gong-shui-san-xie-yun-yong-er-fen-zhao-f-5jyj/) | 简单 | 🤩🤩🤩🤩🤩 |
|
||||
| [778. 水位上升的泳池中游泳](https://leetcode-cn.com/problems/swim-in-rising-water/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/swim-in-rising-water/solution/gong-shui-san-xie-yi-ti-shuang-jie-krusk-7c6o/) | 困难 | 🤩🤩🤩 |
|
||||
| [852. 山脉数组的峰顶索引](https://leetcode-cn.com/problems/peak-index-in-a-mountain-array/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/peak-index-in-a-mountain-array/solution/gong-shui-san-xie-er-fen-san-fen-cha-zhi-5gfv/) | 简单 | 🤩🤩🤩🤩🤩 |
|
||||
| [981. 基于时间的键值存储](https://leetcode-cn.com/problems/time-based-key-value-store/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/time-based-key-value-store/solution/gong-shui-san-xie-yi-ti-shuang-jie-ha-xi-h5et/) | 中等 | 🤩🤩🤩🤩 |
|
||||
| [1004. 最大连续1的个数 III](https://leetcode-cn.com/problems/max-consecutive-ones-iii/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/max-consecutive-ones-iii/solution/san-chong-jie-fa-cong-dong-tai-gui-hua-d-gxks/) | 中等 | 🤩🤩🤩 |
|
||||
| [1011. 在 D 天内送达包裹的能力](https://leetcode-cn.com/problems/capacity-to-ship-packages-within-d-days/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/capacity-to-ship-packages-within-d-days/solution/gong-shui-san-xie-li-yong-er-duan-xing-z-95zj/) | 中等 | 🤩🤩🤩🤩 |
|
||||
| [1208. 尽可能使字符串相等](https://leetcode-cn.com/problems/get-equal-substrings-within-budget/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/get-equal-substrings-within-budget/solution/ni-bu-ke-neng-kan-bu-dong-de-qian-zhui-h-u4l1/) | 中等 | 🤩🤩🤩 |
|
||||
| [1337. 矩阵中战斗力最弱的 K 行](https://leetcode-cn.com/problems/the-k-weakest-rows-in-a-matrix/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/the-k-weakest-rows-in-a-matrix/solution/gong-shui-san-xie-yi-ti-shuang-jie-po-su-7okx/) | 简单 | 🤩🤩🤩 |
|
||||
| [1438. 绝对差不超过限制的最长连续子数组](https://leetcode-cn.com/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/solution/xiang-jie-er-fen-hua-dong-chuang-kou-dan-41g1/) | 中等 | 🤩🤩🤩 |
|
||||
| [1482. 制作 m 束花所需的最少天数](https://leetcode-cn.com/problems/minimum-number-of-days-to-make-m-bouquets/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/minimum-number-of-days-to-make-m-bouquets/solution/gong-shui-san-xie-li-yong-er-duan-xing-z-ysv4/) | 中等 | 🤩🤩🤩 |
|
||||
| [1707. 与数组中元素的最大异或值](https://leetcode-cn.com/problems/maximum-xor-with-an-element-from-array/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/maximum-xor-with-an-element-from-array/solution/gong-shui-san-xie-jie-zhe-ge-wen-ti-lai-lypqr/) | 困难 | 🤩🤩🤩 |
|
||||
| [1713. 得到子序列的最少操作次数](https://leetcode-cn.com/problems/minimum-operations-to-make-a-subsequence/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/minimum-operations-to-make-a-subsequence/solution/gong-shui-san-xie-noxiang-xin-ke-xue-xi-oj7yu/) | 困难 | 🤩🤩🤩 |
|
||||
| [1751. 最多可以参加的会议数目 II](https://leetcode-cn.com/problems/maximum-number-of-events-that-can-be-attended-ii/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/maximum-number-of-events-that-can-be-attended-ii/solution/po-su-dp-er-fen-dp-jie-fa-by-ac_oier-88du/) | 困难 | 🤩🤩🤩 |
|
||||
| [1818. 绝对差值和](https://leetcode-cn.com/problems/minimum-absolute-sum-difference/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/minimum-absolute-sum-difference/solution/gong-shui-san-xie-tong-guo-er-fen-zhao-z-vrmq/) | 中等 | 🤩🤩🤩🤩🤩 |
|
||||
| [1838. 最高频元素的频数](https://leetcode-cn.com/problems/frequency-of-the-most-frequent-element/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/frequency-of-the-most-frequent-element/solution/gong-shui-san-xie-cong-mei-ju-dao-pai-xu-kxnk/) | 中等 | 🤩🤩🤩 |
|
||||
| [1894. 找到需要补充粉笔的学生编号](https://leetcode-cn.com/problems/find-the-student-that-will-replace-the-chalk/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/find-the-student-that-will-replace-the-chalk/solution/gong-shui-san-xie-yi-ti-shuang-jie-qian-kpqsk/) | 中等 | 🤩🤩🤩🤩 |
|
||||
| [剑指 Offer 53 - I. 在排序数组中查找数字 I](https://leetcode-cn.com/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/solution/gong-shui-san-xie-liang-chong-er-fen-ton-3epx/) | 简单 | 🤩🤩🤩🤩🤩 |
|
||||
|
||||
**注:以上目录整理来自 [wiki](https://github.com/SharingSource/LogicStack-LeetCode/wiki/二分),任何形式的转载引用请保留出处。**
|
||||
@ -0,0 +1,89 @@
|
||||
## 数学
|
||||
|
||||
一个不能再朴素的做法是将 $n$ 对 $3$ 进行试除,直到 $n$ 不再与 $3$ 呈倍数关系,最后判断 $n$ 是否为 $3^0 = 1$ 即可。
|
||||
|
||||
代码:
|
||||
|
||||
* Java
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public boolean isPowerOfThree(int n) {
|
||||
if (n <= 0) return false;
|
||||
while (n % 3 == 0) n /= 3;
|
||||
return n == 1;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(\log_{3}n)$
|
||||
* 空间复杂度:$O(1)$
|
||||
|
||||
---
|
||||
|
||||
## 倍数 & 约数
|
||||
|
||||
题目要求不能使用循环或递归来做,而传参 $n$ 的数据类型为 `int`,这引导我们首先分析出 `int` 范围内的最大 $3$ 次幂是多少,约为 $3^{19} = 1162261467$。
|
||||
|
||||
如果 $n$ 为 $3$ 的幂的话,那么必然满足 $n * 3^k = 1162261467$,即 $n$ 与 $1162261467$ 存在倍数关系。
|
||||
|
||||
因此,我们只需要判断 $n$ 是否为 $1162261467$ 的约数即可。
|
||||
|
||||
代码:
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public boolean isPowerOfThree(int n) {
|
||||
return n > 0 && 1162261467 % n == 0;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(1)$
|
||||
* 空间复杂度:$O(1)$
|
||||
|
||||
---
|
||||
|
||||
## 打表
|
||||
|
||||
另外一个更容易想到的「不使用循环/递归」的做法是进行打表预处理。
|
||||
|
||||
使用 `static` 代码块,预处理出不超过 `int` 数据范围的所有 $3$ 的幂,这样我们在跑测试样例时,就不需要使用「循环/递归」来实现逻辑,可直接 $O(1)$ 查表返回。
|
||||
|
||||
代码:
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
static Set<Integer> set = new HashSet<>();
|
||||
static {
|
||||
int cur = 1;
|
||||
set.add(cur);
|
||||
while (cur <= Integer.MAX_VALUE / 3) {
|
||||
cur *= 3;
|
||||
set.add(cur);
|
||||
}
|
||||
}
|
||||
public boolean isPowerOfThree(int n) {
|
||||
return n > 0 && set.contains(n);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* 时间复杂度:将打表逻辑交给 $OJ$ 执行的话,复杂度为 $O(\log_3{C})$,$C$ 固定为 $2147483647$;将打表逻辑放到本地执行,复杂度为 $O(1)$
|
||||
* 空间复杂度:$O(n)$
|
||||
|
||||
---
|
||||
|
||||
## 其他「$x$ 的幂」问题
|
||||
|
||||
可以尝试加练如下的「$x$ 的幂」问题 🍭🍭🍭
|
||||
|
||||
| 题目 | 题解 | 难度 | 推荐指数 |
|
||||
| ------------------------------------------------------------ | ------------------------------------------------------------ | ---- | -------- |
|
||||
| [231. 2 的幂](https://leetcode-cn.com/problems/power-of-two/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/power-of-two/solution/gong-shui-san-xie-2-de-mi-by-ac_oier-qm6e/) | 简单 | 🤩🤩🤩🤩 |
|
||||
| [342. 4的幂](https://leetcode-cn.com/problems/power-of-four/) | [LeetCode 题解链接](https://leetcode-cn.com/problems/power-of-four/solution/gong-shui-san-xie-zhuan-hua-wei-2-de-mi-y21lq/) | 简单 | 🤩🤩🤩🤩 |
|
||||
|
||||
@ -0,0 +1,45 @@
|
||||
最新价格从《时间-价格表》HashMap中取
|
||||
最大最小值从 《价格-数量表》TreeMap中取
|
||||
|
||||
|
||||
*
|
||||
|
||||
```
|
||||
class StockPrice {
|
||||
HashMap<Integer, Integer> tsMap;
|
||||
TreeMap<Integer, Integer> priceMap;
|
||||
int currentTs;
|
||||
|
||||
public StockPrice() {
|
||||
tsMap = new HashMap<>();
|
||||
priceMap = new TreeMap<>();
|
||||
currentTs = 0;
|
||||
}
|
||||
|
||||
public void update(int timestamp, int price) {
|
||||
if (tsMap.containsKey(timestamp)) {
|
||||
int oldPrice = tsMap.get(timestamp);
|
||||
priceMap.put(oldPrice, priceMap.get(oldPrice) - 1);
|
||||
if (priceMap.get(oldPrice) == 0) {
|
||||
priceMap.remove(oldPrice);
|
||||
}
|
||||
}
|
||||
priceMap.put(price, priceMap.getOrDefault(price, 0) + 1);
|
||||
tsMap.put(timestamp, price);
|
||||
currentTs = Math.max(currentTs, timestamp);
|
||||
}
|
||||
|
||||
public int current() {
|
||||
return tsMap.get(currentTs);
|
||||
}
|
||||
|
||||
public int maximum() {
|
||||
return priceMap.lastKey();
|
||||
}
|
||||
|
||||
public int minimum() {
|
||||
return priceMap.firstKey();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -0,0 +1,151 @@
|
||||
#### 方法一:利用堆的贪心算法
|
||||
|
||||
**思路与算法**
|
||||
|
||||
我们首先思考,如果不限制次数下我们可以获取的最大利润,我们应该如何处理?我们只需将所有的项目按照资本的大小进行排序,依次购入项目 $i$,同时手中持有的资本增加 $\textit{profits}[i]$,直到手中的持有的资本无法启动当前的项目为止。
|
||||
|
||||
+ 如果初始资本 $w \ge \max(\textit{capital})$,我们直接返回利润中的 $k$ 个最大元素的和即可。
|
||||
|
||||
+ 当前的题目中限定了可以选择的次数最多为 $k$ 次,这就意味着我们应该贪心地保证选择每次投资的项目获取的利润最大,这样就能保持选择 $k$ 次后获取的利润最大。
|
||||
|
||||
+ 我们首先将项目按照所需资本的从小到大进行排序,每次进行选择时,假设当前手中持有的资本为 $w$,我们应该从所有投入资本小于等于 $w$ 的项目中选择利润最大的项目 $j$,然后此时我们更新手中持有的资本为 $w + \textit{profits}[j]$,同时再从所有花费资本小于等于 $w + \textit{profits}[j]$ 的项目中选择,我们按照上述规则不断选择 $k$ 次即可。
|
||||
|
||||
+ 我们利用大根堆的特性,我们将所有能够投资的项目的利润全部压入到堆中,每次从堆中取出最大值,然后更新手中持有的资本,同时将待选的项目利润进入堆,不断重复上述操作。
|
||||
|
||||
+ 如果当前的堆为空,则此时我们应当直接返回。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
typedef pair<int,int> pii;
|
||||
|
||||
class Solution {
|
||||
public:
|
||||
int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {
|
||||
int n = profits.size();
|
||||
int curr = 0;
|
||||
priority_queue<int, vector<int>, less<int>> pq;
|
||||
vector<pii> arr;
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
arr.push_back({capital[i], profits[i]});
|
||||
}
|
||||
sort(arr.begin(), arr.end());
|
||||
for (int i = 0; i < k; ++i) {
|
||||
while (curr < n && arr[curr].first <= w) {
|
||||
pq.push(arr[curr].second);
|
||||
curr++;
|
||||
}
|
||||
if (!pq.empty()) {
|
||||
w += pq.top();
|
||||
pq.pop();
|
||||
} else {
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
return w;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
|
||||
int n = profits.length;
|
||||
int curr = 0;
|
||||
int[][] arr = new int[n][2];
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
arr[i][0] = capital[i];
|
||||
arr[i][1] = profits[i];
|
||||
}
|
||||
Arrays.sort(arr, (a, b) -> a[0] - b[0]);
|
||||
|
||||
PriorityQueue<Integer> pq = new PriorityQueue<>((x, y) -> y - x);
|
||||
for (int i = 0; i < k; ++i) {
|
||||
while (curr < n && arr[curr][0] <= w) {
|
||||
pq.add(arr[curr][1]);
|
||||
curr++;
|
||||
}
|
||||
if (!pq.isEmpty()) {
|
||||
w += pq.poll();
|
||||
} else {
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
return w;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def findMaximizedCapital(self, k: int, w: int, profits: List[int], capital: List[int]) -> int:
|
||||
if w >= max(capital):
|
||||
return w + sum(nlargest(k, profits))
|
||||
|
||||
n = len(profits)
|
||||
curr = 0
|
||||
arr = [(capital[i], profits[i]) for i in range(n)]
|
||||
arr.sort(key = lambda x : x[0])
|
||||
|
||||
pq = []
|
||||
for _ in range(k):
|
||||
while curr < n and arr[curr][0] <= w:
|
||||
heappush(pq, -arr[curr][1])
|
||||
curr += 1
|
||||
|
||||
if pq:
|
||||
w -= heappop(pq)
|
||||
else:
|
||||
break
|
||||
|
||||
return w
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func findMaximizedCapital(k, w int, profits, capital []int) int {
|
||||
n := len(profits)
|
||||
type pair struct{ c, p int }
|
||||
arr := make([]pair, n)
|
||||
for i, p := range profits {
|
||||
arr[i] = pair{capital[i], p}
|
||||
}
|
||||
sort.Slice(arr, func(i, j int) bool { return arr[i].c < arr[j].c })
|
||||
|
||||
h := &hp{}
|
||||
for cur := 0; k > 0; k-- {
|
||||
for cur < n && arr[cur].c <= w {
|
||||
heap.Push(h, arr[cur].p)
|
||||
cur++
|
||||
}
|
||||
if h.Len() == 0 {
|
||||
break
|
||||
}
|
||||
w += heap.Pop(h).(int)
|
||||
}
|
||||
return w
|
||||
}
|
||||
|
||||
type hp struct{ sort.IntSlice }
|
||||
func (h hp) Less(i, j int) bool { return h.IntSlice[i] > h.IntSlice[j] }
|
||||
func (h *hp) Push(v interface{}) { h.IntSlice = append(h.IntSlice, v.(int)) }
|
||||
func (h *hp) Pop() interface{} { a := h.IntSlice; v := a[len(a)-1]; h.IntSlice = a[:len(a)-1]; return v }
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O((n + k) \log n)$,其中 $n$ 是数组 $\textit{profits}$ 和 $\textit{capital}$ 的长度,$k$ 表示最多的选择数目。我们需要 $O(n \log n)$ 的时间复杂度来来创建和排序项目,往堆中添加元素的时间不超过 $O(n \log n)$,每次从堆中取出最大值并更新资本的时间为 $O(k \log n)$,因此总的时间复杂度为 $O(n \log n + n \log n + k \log n) = O((n + k) \log n)$。
|
||||
|
||||
- 空间复杂度:$O(n)$,其中 $n$ 是数组 $\textit{profits}$ 和 $\textit{capital}$ 的长度。空间复杂度主要取决于创建用于排序的数组和大根堆。
|
||||
|
||||
@ -0,0 +1,77 @@
|
||||

|
||||
|
||||
# 如果视频失效,还请到B站观看 https://space.bilibili.com/479038960
|
||||
|
||||
# code
|
||||
|
||||
* java
|
||||
|
||||
```java
|
||||
/*
|
||||
|
||||
1. 定界限
|
||||
n = 2
|
||||
int upperBound = 99 99 / 10 + 1
|
||||
int lowerBound = 10
|
||||
|
||||
2.手动生成回文串
|
||||
long maxNumber = 99 * 99 = 9801 9889
|
||||
9779
|
||||
9669
|
||||
9559
|
||||
|
||||
|
||||
1001
|
||||
手动生成 98 89
|
||||
|
||||
3.
|
||||
判断, 是否回文串
|
||||
|
||||
4.
|
||||
return
|
||||
|
||||
|
||||
1 --> 9 1 .... 81
|
||||
|
||||
77 66 55 44 33 22 11
|
||||
7 * 11 3 * 11
|
||||
*/
|
||||
public int largestPalindrome(int n) {
|
||||
if(n == 1)
|
||||
return 9;
|
||||
|
||||
long upperBound = (long)Math.pow(10, n) - 1;
|
||||
long lowerBound = upperBound / 10 + 1;
|
||||
|
||||
long maxNumber = upperBound * upperBound; //9801
|
||||
long half = (long)(maxNumber / (Math.pow(10, n))); //98 89
|
||||
|
||||
boolean found = false;
|
||||
long res = 0;
|
||||
|
||||
while(!found){
|
||||
res = createPalindrome(half);
|
||||
for(long i = upperBound; i >= lowerBound; i--){
|
||||
if(i * i < res)
|
||||
break;
|
||||
|
||||
if(res % i == 0){
|
||||
found = true;
|
||||
break;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
half--;
|
||||
}
|
||||
|
||||
return (int)(res % 1337);
|
||||
}
|
||||
|
||||
private long createPalindrome(long num) {
|
||||
String pStr = num + new StringBuilder().append(num).reverse().toString();
|
||||
return Long.parseLong(pStr);
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
@ -0,0 +1,78 @@
|
||||
### 解题思路
|
||||
|
||||
|
||||
|
||||
遍历words,一行一行进行处理。
|
||||
|
||||
对words中的单词进行读取,用curlen记录读取的长度,curlen>maxWidth时进行排版处理。
|
||||
当curlen>maxWidth时证明已经多读了一个单词了,所以要减去最后读取的单词长度。
|
||||
此时curlen<maxWidth的差值就是需要补的空格数。
|
||||
|
||||
排版时:计算出该行总共的空格数:addSpace,以及间隙数:map
|
||||
allAddSpace = addSpace/map; 为每个间隙必加的最少空格数;
|
||||
left = addSpace % map + si; 为余出来的空格数,要从si开始,依次加在间隙中
|
||||
|
||||
排版时要注意“只有一个单词”,以及“最后一行”,这两种特殊情况。
|
||||
|
||||
### 代码
|
||||
|
||||
* java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public List<String> fullJustify(String[] words, int maxWidth) {
|
||||
//定义0-maxWidth个空格字符串,方便之后直接调用
|
||||
final String[] space = new String[maxWidth+1];
|
||||
StringBuffer s = new StringBuffer();
|
||||
for(int i = 0;i<maxWidth+1;i++){
|
||||
space[i] = s.toString();
|
||||
s.append(" ");
|
||||
}
|
||||
//新建List,用来存最后的结果。
|
||||
List<String> pWords = new ArrayList<String>();
|
||||
//遍历整个words,一行一行的排版
|
||||
for(int i=0; i<words.length; i++){
|
||||
int curlen = words[i].length(); //记录当前已读取单词的长度,当>=maxWidth时进行排版
|
||||
int startI = i; //记录本次读取单词的起点
|
||||
while(i < words.length-1 && curlen<maxWidth){
|
||||
i++;
|
||||
curlen = curlen+words[i].length()+1; // 每多读一个单词都要加一个空格
|
||||
}
|
||||
if(curlen>maxWidth){ //当前长度>maxWidth,说明已经多读取了一个单词
|
||||
curlen = curlen-words[i].length()-1;
|
||||
i--;
|
||||
}
|
||||
//一行一行的排版
|
||||
pWords.add(processCurline(words,startI,i,curlen,maxWidth,space));
|
||||
}
|
||||
return pWords;
|
||||
}
|
||||
public String processCurline(String[] words,int si,int ei,int curlen,int maxWidth,String[] space){
|
||||
StringBuffer sb = new StringBuffer(); //用来进行排版
|
||||
int map = ei-si; // 记录单词之间的有几个间隙
|
||||
int addSpace = maxWidth - curlen+map; //记录这一行总共有多少个空格
|
||||
if(map==0){ //间隙为0,证明只有一个单词
|
||||
sb.append(words[ei]);
|
||||
sb.append(space[addSpace]);
|
||||
return sb.toString();
|
||||
}
|
||||
if(ei == words.length-1){ //证明要排版最后一行了,格式特殊
|
||||
for(int i =si;i<ei;i++){
|
||||
sb.append(words[i]).append(" ");
|
||||
}
|
||||
sb.append(words[ei]); //最后一个单词不用加空格
|
||||
sb.append(space[addSpace-map]); //如果还有多余空格,一起加上
|
||||
return sb.toString();
|
||||
}
|
||||
int allAddSpace = addSpace/map; //所有的空格数 / 间隙 = 每个间隙必加的空格数
|
||||
int left = addSpace % map + si; //多出来的空格要从si开始,依次加在间隙中
|
||||
for(int i = si;i<ei;i++){
|
||||
sb.append(words[i]).append(space[allAddSpace]);
|
||||
if(i < left) sb.append(" "); // <left就要多加一个空格
|
||||
}
|
||||
sb.append(words[ei]);
|
||||
return sb.toString();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -0,0 +1,211 @@
|
||||
# 前言
|
||||
|
||||
本题是寻找最短路径问题,可以分别采用【并查集/Kruskal】、【二分dfs/bfs】、【Dijkstra】进行解决
|
||||
**并查集**
|
||||
并查集中首先采用 Kruskal 最小生成树方法,以相邻结点的高度差作为权值,然后根据权值从小到大的顺序构图,直到左上角结点和右下角结点连通,break,输出结果。
|
||||
**二分法**
|
||||
图的问题也可以采用dfs和bfs进行求解,题目注释里给出高度值的范围为[1,1000000],因此结果最大为100000,可以采用二分法进行夹逼求得结果。注意:如果不采用二分法,而是采用传统回溯法,会导致超时
|
||||
**dijkstra**
|
||||
最短路径问题,可以联想到使用 dijkstra 算法进行求解
|
||||
|
||||
各解法代码及注释如下
|
||||
|
||||
* []
|
||||
|
||||
```并查集
|
||||
class Solution {
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
int rows = heights.length;
|
||||
int cols = heights[0].length;
|
||||
//Kruskal构造连边
|
||||
List<int[]> edges = new LinkedList<>();
|
||||
for(int i=0;i<rows;i++){
|
||||
for(int j=0;j<cols;j++){
|
||||
int id = i*cols+j;
|
||||
if(i<rows-1){
|
||||
edges.add(new int[]{id,id+cols,Math.abs(heights[i][j]-heights[i+1][j])});
|
||||
}
|
||||
if(j<cols-1){
|
||||
edges.add(new int[]{id,id+1,Math.abs(heights[i][j]-heights[i][j+1])});
|
||||
}
|
||||
}
|
||||
}
|
||||
//根据结点之间的权值进行排序
|
||||
Collections.sort(edges,new Comparator<int[]>(){
|
||||
public int compare(int[] o1,int[] o2){
|
||||
return o1[2] - o2[2];
|
||||
}
|
||||
});
|
||||
int ans = 0;
|
||||
//从小到大连通结点
|
||||
UnionFind uf = new UnionFind(rows*cols);
|
||||
for(int i=0;i<edges.size();i++){
|
||||
int[] temp = edges.get(i);
|
||||
int x = temp[0];
|
||||
int y = temp[1];
|
||||
int dp = temp[2];
|
||||
if(uf.find(x)!=uf.find(y)){
|
||||
uf.union(x,y);
|
||||
ans = dp;
|
||||
}
|
||||
//左上角结点和右下角结点连通
|
||||
if(uf.find(0)==uf.find(rows*cols-1)){
|
||||
break;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
//并查集
|
||||
class UnionFind{
|
||||
int[] f;
|
||||
public UnionFind(int n){
|
||||
f = new int[n];
|
||||
for(int i=0;i<n;i++){
|
||||
f[i] = i;
|
||||
}
|
||||
}
|
||||
//查
|
||||
public int find(int x){
|
||||
if(f[x]!=x){
|
||||
f[x] = find(f[x]);
|
||||
}
|
||||
return f[x];
|
||||
}
|
||||
//并
|
||||
public void union(int x,int y){
|
||||
if(find(x)!=find(y)){
|
||||
f[find(x)] = find(y);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* []
|
||||
|
||||
```二分法dfs
|
||||
class Solution {
|
||||
int[][] directions = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
|
||||
int ans = Integer.MAX_VALUE;
|
||||
int rows;
|
||||
int cols;
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
rows = heights.length;
|
||||
cols = heights[0].length;
|
||||
int left = 0;
|
||||
int right = 1000000;
|
||||
while(left<right){
|
||||
int mid = (right+left)/2;
|
||||
//更新左右边界
|
||||
if(dfs(heights,0,0,mid,new boolean[rows][cols])){
|
||||
right = mid;
|
||||
}else{
|
||||
left = mid+1;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
}
|
||||
//dfs寻找是否存在一条连通左上角和右下角结点的道路
|
||||
public Boolean dfs(int[][] heights,int row,int col,int mid,boolean[][] visited){
|
||||
if(row==rows-1 && col==cols-1){
|
||||
return true;
|
||||
}
|
||||
visited[row][col] = true;
|
||||
for(int[] dir:directions){
|
||||
int newRow = row + dir[0];
|
||||
int newCol = col + dir[1];
|
||||
if(newRow>=0&&newRow<rows&&newCol>=0&&newCol<cols && !visited[newRow][newCol] &&
|
||||
Math.abs(heights[newRow][newCol]-heights[row][col])<=mid){
|
||||
if(dfs(heights,newRow,newCol,mid,visited)) return true;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* []
|
||||
|
||||
```二分法bfs
|
||||
class Solution {
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
int[][] directions = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
|
||||
int rows = heights.length;
|
||||
int cols = heights[0].length;
|
||||
int left = 0,right = 1000000;
|
||||
while(left<right){
|
||||
int mid = (left+right)/2;
|
||||
boolean[][] visited = new boolean[rows][cols];
|
||||
Queue<int[]> queue = new LinkedList<>();
|
||||
queue.offer(new int[]{0,0});
|
||||
visited[0][0] = true;
|
||||
while(!queue.isEmpty()){
|
||||
int[] temp = queue.poll();
|
||||
int x = temp[0];
|
||||
int y = temp[1];
|
||||
for(int[] dir:directions){
|
||||
int nx = x+dir[0];
|
||||
int ny = y+dir[1];
|
||||
if(nx>=0 && nx<rows && ny>=0 && ny<cols && !visited[nx][ny]
|
||||
&& Math.abs(heights[nx][ny]-heights[x][y])<=mid){
|
||||
queue.offer(new int[]{nx,ny});
|
||||
visited[nx][ny] = true;
|
||||
}
|
||||
}
|
||||
}
|
||||
if(visited[rows-1][cols-1]){
|
||||
right = mid;
|
||||
}else{
|
||||
left = mid+1;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* []
|
||||
|
||||
```dijkstra
|
||||
class Solution {
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
int[][] directions = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
|
||||
int rows = heights.length;
|
||||
int cols = heights[0].length;
|
||||
//优先队列,最小的先出来
|
||||
PriorityQueue<int[]> queue = new PriorityQueue<>(new Comparator<int[]>(){
|
||||
public int compare(int[] o1,int[] o2){
|
||||
return o1[2] - o2[2];
|
||||
}
|
||||
});
|
||||
boolean[][] visited = new boolean[rows][cols];
|
||||
int[] dist = new int[rows*cols];
|
||||
Arrays.fill(dist,Integer.MAX_VALUE);
|
||||
dist[0] = 0;
|
||||
queue.offer(new int[]{0,0,0});
|
||||
while(!queue.isEmpty()){
|
||||
int[] temp = queue.poll();
|
||||
int x = temp[0];
|
||||
int y = temp[1];
|
||||
int dp = temp[2];
|
||||
if(visited[x][y]) continue;
|
||||
if(x==rows-1 && y==cols-1){
|
||||
break;
|
||||
}
|
||||
//弹出来之后再进行标记,确定此刻为最小
|
||||
visited[x][y] = true;
|
||||
for(int[] dir:directions){
|
||||
int nx = x+dir[0];
|
||||
int ny = y+dir[1];
|
||||
if(nx>=0 && nx<rows && ny>=0 && ny<cols
|
||||
&& Math.max(dp,Math.abs(heights[nx][ny]-heights[x][y]))<=dist[nx*cols+ny]){
|
||||
dist[nx*cols+ny] = Math.max(dp,Math.abs(heights[nx][ny]-heights[x][y]));
|
||||
queue.offer(new int[]{nx,ny,dist[nx*cols+ny]});
|
||||
}
|
||||
}
|
||||
}
|
||||
return dist[rows*cols-1];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -0,0 +1,190 @@
|
||||
### 解题思路:
|
||||
|
||||
最短路径:基于 `dijkstra` 算法(127ms)
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
int m = heights.length, n = heights[0].length;
|
||||
int[][] dist = new int[m][n];
|
||||
int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
|
||||
for(int[] d : dist)
|
||||
Arrays.fill(d, Integer.MAX_VALUE);
|
||||
dist[0][0] = 0;
|
||||
Queue<int[]> queue = new PriorityQueue<>((a, b) -> a[2] - b[2]);
|
||||
boolean[][] visited = new boolean[m][n];
|
||||
queue.offer(new int[]{0, 0, 0});
|
||||
while(!queue.isEmpty()) {
|
||||
int[] cur = queue.poll();
|
||||
int x = cur[0], y = cur[1];
|
||||
if(visited[x][y])
|
||||
continue;
|
||||
visited[x][y] = true;
|
||||
for(int[] d : dir) {
|
||||
int nx = x + d[0], ny = y + d[1];
|
||||
if(0 <= nx && nx < m && 0 <= ny && ny < n) {
|
||||
int effort = Math.max(dist[x][y], Math.abs(heights[x][y] - heights[nx][ny]));
|
||||
dist[nx][ny] = Math.min(dist[nx][ny], effort);
|
||||
queue.offer(new int[]{nx, ny, dist[nx][ny]});
|
||||
}
|
||||
}
|
||||
}
|
||||
return dist[m-1][n-1];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
最小生成树:基于并查集(96ms)
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
private int m;
|
||||
private int n;
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
m = heights.length;
|
||||
n = heights[0].length;
|
||||
parent = new int[m * n];
|
||||
rank = new int[m * n];
|
||||
for (int i = 0; i < parent.length; i++) {
|
||||
parent[i] = i;
|
||||
rank[i] = 1;
|
||||
}
|
||||
List<Edge> list = new ArrayList<>();
|
||||
for(int i = 0; i < m; i++) {
|
||||
for(int j = 0; j < n; j++) {
|
||||
if(i + 1 < m){
|
||||
list.add(new Edge(i*n+j, (i+1)*n+j, Math.abs(heights[i][j] - heights[i+1][j])));
|
||||
}
|
||||
if(j + 1 < n){
|
||||
list.add(new Edge(i*n+j, i*n+j+1, Math.abs(heights[i][j] - heights[i][j+1])));
|
||||
}
|
||||
}
|
||||
}
|
||||
Collections.sort(list, (a, b) -> a.value - b.value);
|
||||
int ret = 0;
|
||||
for(Edge edge : list){
|
||||
if(isConnected(0, m*n-1))
|
||||
break;
|
||||
int v = edge.v, w = edge.w;
|
||||
if(!isConnected(v, w)){
|
||||
unionElements(v, w);
|
||||
ret = edge.value;
|
||||
}
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
class Edge{
|
||||
int v;
|
||||
int w;
|
||||
int value;
|
||||
Edge(int v, int w, int value) {
|
||||
this.v = v;
|
||||
this.w = w;
|
||||
this.value = value;
|
||||
}
|
||||
}
|
||||
private int[] parent;
|
||||
private int[] rank;
|
||||
private int find(int p){
|
||||
if (p != parent[p])
|
||||
parent[p] = find(parent[p]);
|
||||
return parent[p];
|
||||
}
|
||||
private boolean isConnected(int p, int q) {
|
||||
return find(p) == find(q);
|
||||
}
|
||||
public void unionElements(int p, int q) {
|
||||
int pRoot = find(p);
|
||||
int qRoot = find(q);
|
||||
if(pRoot == qRoot)
|
||||
return;
|
||||
if(rank[pRoot] < rank[qRoot])
|
||||
parent[pRoot] = qRoot;
|
||||
else if(rank[pRoot] > rank[qRoot])
|
||||
parent[qRoot] = pRoot;
|
||||
else {
|
||||
parent[qRoot] = pRoot;
|
||||
rank[pRoot] += 1;
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
二分答案:基于DFS(74ms)
|
||||
|
||||
* java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
private int m;
|
||||
private int n;
|
||||
private int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
m = heights.length;
|
||||
n = heights[0].length;
|
||||
int l = 0, r = 1000000;
|
||||
while(l < r) {
|
||||
int mid = l + r >>> 1;
|
||||
if(!dfs(0, 0, mid, heights, new boolean[m][n]))
|
||||
l = mid + 1;
|
||||
else
|
||||
r = mid;
|
||||
}
|
||||
return l;
|
||||
}
|
||||
private boolean dfs(int x, int y, int effort, int[][] heights, boolean[][] visited) {
|
||||
if(x == m - 1 && y == n - 1)
|
||||
return true;
|
||||
visited[x][y] = true;
|
||||
for(int[] d : dir) {
|
||||
int nx = x + d[0], ny = y + d[1];
|
||||
if(0 <= nx && nx < m && 0 <= ny && ny < n && !visited[nx][ny]) {
|
||||
if(Math.abs(heights[nx][ny] - heights[x][y]) > effort)
|
||||
continue;
|
||||
if(dfs(nx, ny, effort, heights, visited))
|
||||
return true;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
BFS:备忘录优化(101ms)
|
||||
|
||||
* []
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
int m = heights.length, n = heights[0].length;
|
||||
int[][] memo = new int[m][n];
|
||||
int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
|
||||
for(int[] arr : memo)
|
||||
Arrays.fill(arr, Integer.MAX_VALUE);
|
||||
memo[0][0] = 0;
|
||||
Queue<Integer> queue = new LinkedList<>();
|
||||
queue.offer(0);
|
||||
while(!queue.isEmpty()) {
|
||||
int cur = queue.poll();
|
||||
int x = cur / n, y = cur % n;
|
||||
for(int[] d : dir) {
|
||||
int nx = x + d[0], ny = y + d[1];
|
||||
if(0 <= nx && nx < m && 0 <= ny && ny < n) {
|
||||
int effort = Math.max(memo[x][y], Math.abs(heights[nx][ny] - heights[x][y]));
|
||||
if(effort >= memo[nx][ny])
|
||||
continue;
|
||||
memo[nx][ny] = effort;
|
||||
queue.offer(nx * n + ny);
|
||||
}
|
||||
}
|
||||
}
|
||||
return memo[m-1][n-1];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -0,0 +1,29 @@
|
||||
思路:其实没啥思路,就是简单的获得中位数,在进行加减x等于中位数的操作
|
||||

|
||||
|
||||
*
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public int minOperations(int[][] grid, int x) {
|
||||
int n = grid.length;
|
||||
int m = grid[0].length;
|
||||
int[] arr = new int[m*n];
|
||||
int i = 0;
|
||||
for(int[] a : grid)
|
||||
for(int a_ : a){
|
||||
arr[i++] = a_;
|
||||
}
|
||||
Arrays.sort(arr);
|
||||
int j = arr[(n*m)/2];
|
||||
int sum = 0;
|
||||
for(int a : arr){
|
||||
int l = Math.abs(j-a);
|
||||
if(l%x != 0) return -1;
|
||||
sum += l/x;
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -0,0 +1,184 @@
|
||||
#### 方法一:动态规划
|
||||
|
||||
**思路与算法**
|
||||
|
||||
本题以二叉树为背景,不难想到用递归的方式求解。本题的难度在于如何从左、右子树的状态,推导出父节点的状态。
|
||||
|
||||
为了表述方便,我们约定:如果某棵树的所有节点都被监控,则称该树被「覆盖」。
|
||||
|
||||
假设当前节点为 $\textit{root}$,其左右孩子为 $\textit{left}, \textit{right}$。如果要覆盖以 $\textit{root}$ 为根的树,有两种情况:
|
||||
- 若在 $\textit{root}$ 处安放摄像头,则孩子 $\textit{left}, \textit{right}$ 一定也会被监控到。此时,只需要保证 $\textit{left}$ 的两棵子树被覆盖,同时保证 $\textit{right}$ 的两棵子树也被覆盖即可。
|
||||
- 否则, 如果 $\textit{root}$ 处不安放摄像头,则除了覆盖 $\textit{root}$ 的两棵子树之外,孩子 $\textit{left}, \textit{right}$ 之一必须要安装摄像头,从而保证 $\textit{root}$ 会被监控到。
|
||||
|
||||
根据上面的讨论,能够分析出,对于每个节点 $\textit{root}$ ,需要维护三种类型的状态:
|
||||
- 状态 $a$:$\textit{root}$ 必须放置摄像头的情况下,覆盖整棵树需要的摄像头数目。
|
||||
- 状态 $b$:覆盖整棵树需要的摄像头数目,无论 $\textit{root}$ 是否放置摄像头。
|
||||
- 状态 $c$:覆盖两棵子树需要的摄像头数目,无论节点 $\textit{root}$ 本身是否被监控到。
|
||||
|
||||
根据它们的定义,一定有 $a \geq b \geq c$。
|
||||
|
||||
对于节点 $\textit{root}$ 而言,设其左右孩子 $\textit{left}, \textit{right}$ 对应的状态变量分别为 $(l_a,l_b,l_c)$ 以及 $(r_a,r_b,r_c)$。根据一开始的讨论,我们已经得到了求解 $a,b$ 的过程:
|
||||
- $a = l_c + r_c + 1$
|
||||
- $b = \min(a, \min(l_a + r_b, r_a + l_b))$
|
||||
|
||||
对于 $c$ 而言,要保证两棵子树被完全覆盖,要么 $\textit{root}$ 处放置一个摄像头,需要的摄像头数目为 $a$;要么 $\textit{root}$ 处不放置摄像头,此时两棵子树分别保证自己被覆盖,需要的摄像头数目为 $l_b + r_b$。
|
||||
|
||||
需要额外注意的是,对于 $\textit{root}$ 而言,如果其某个孩子为空,则不能通过在该孩子处放置摄像头的方式,监控到当前节点。因此,该孩子对应的变量 $a$ 应当返回一个大整数,用于标识不可能的情形。
|
||||
|
||||
最终,根节点的状态变量 $b$ 即为要求出的答案。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
struct Status {
|
||||
int a, b, c;
|
||||
};
|
||||
|
||||
class Solution {
|
||||
public:
|
||||
Status dfs(TreeNode* root) {
|
||||
if (!root) {
|
||||
return {INT_MAX / 2, 0, 0};
|
||||
}
|
||||
auto [la, lb, lc] = dfs(root->left);
|
||||
auto [ra, rb, rc] = dfs(root->right);
|
||||
int a = lc + rc + 1;
|
||||
int b = min(a, min(la + rb, ra + lb));
|
||||
int c = min(a, lb + rb);
|
||||
return {a, b, c};
|
||||
}
|
||||
|
||||
int minCameraCover(TreeNode* root) {
|
||||
auto [a, b, c] = dfs(root);
|
||||
return b;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int minCameraCover(TreeNode root) {
|
||||
int[] array = dfs(root);
|
||||
return array[1];
|
||||
}
|
||||
|
||||
public int[] dfs(TreeNode root) {
|
||||
if (root == null) {
|
||||
return new int[]{Integer.MAX_VALUE / 2, 0, 0};
|
||||
}
|
||||
int[] leftArray = dfs(root.left);
|
||||
int[] rightArray = dfs(root.right);
|
||||
int[] array = new int[3];
|
||||
array[0] = leftArray[2] + rightArray[2] + 1;
|
||||
array[1] = Math.min(array[0], Math.min(leftArray[0] + rightArray[1], rightArray[0] + leftArray[1]));
|
||||
array[2] = Math.min(array[0], leftArray[1] + rightArray[1]);
|
||||
return array;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```Golang
|
||||
const inf = math.MaxInt32 / 2 // 或 math.MaxInt64 / 2
|
||||
|
||||
func minCameraCover(root *TreeNode) int {
|
||||
var dfs func(*TreeNode) (a, b, c int)
|
||||
dfs = func(node *TreeNode) (a, b, c int) {
|
||||
if node == nil {
|
||||
return inf, 0, 0
|
||||
}
|
||||
la, lb, lc := dfs(node.Left)
|
||||
ra, rb, rc := dfs(node.Right)
|
||||
a = lc + rc + 1
|
||||
b = min(a, min(la+rb, ra+lb))
|
||||
c = min(a, lb+rb)
|
||||
return
|
||||
}
|
||||
_, ans, _ := dfs(root)
|
||||
return ans
|
||||
}
|
||||
|
||||
func min(a, b int) int {
|
||||
if a < b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var minCameraCover = function(root) {
|
||||
const dfs = (root) => {
|
||||
if (!root) {
|
||||
return [Math.floor(Number.MAX_SAFE_INTEGER / 2), 0, 0];
|
||||
}
|
||||
const [la, lb, lc] = dfs(root.left);
|
||||
const [ra, rb, rc] = dfs(root.right);
|
||||
const a = lc + rc + 1;
|
||||
const b = Math.min(a, Math.min(la + rb, ra + lb));
|
||||
const c = Math.min(a, lb + rb);
|
||||
return [a, b, c];
|
||||
}
|
||||
|
||||
return dfs(root)[1];
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def minCameraCover(self, root: TreeNode) -> int:
|
||||
def dfs(root: TreeNode) -> List[int]:
|
||||
if not root:
|
||||
return [float("inf"), 0, 0]
|
||||
|
||||
la, lb, lc = dfs(root.left)
|
||||
ra, rb, rc = dfs(root.right)
|
||||
a = lc + rc + 1
|
||||
b = min(a, la + rb, ra + lb)
|
||||
c = min(a, lb + rb)
|
||||
return [a, b, c]
|
||||
|
||||
a, b, c = dfs(root)
|
||||
return b
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
struct Status {
|
||||
int a, b, c;
|
||||
};
|
||||
|
||||
struct Status dfs(struct TreeNode* root) {
|
||||
if (!root) {
|
||||
return (struct Status){INT_MAX / 2, 0, 0};
|
||||
}
|
||||
struct Status l = dfs(root->left);
|
||||
struct Status r = dfs(root->right);
|
||||
int a = l.c + r.c + 1;
|
||||
int b = fmin(a, fmin(l.a + r.b, r.a + l.b));
|
||||
int c = fmin(a, l.b + r.b);
|
||||
return (struct Status){a, b, c};
|
||||
}
|
||||
|
||||
int minCameraCover(struct TreeNode* root) {
|
||||
struct Status ret = dfs(root);
|
||||
return ret.b;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(N)$,其中 $N$ 为树中节点的数量。对于每个节点,我们在常数时间内计算出 $a,b,c$ 三个状态变量。
|
||||
|
||||
- 空间复杂度:$O(N)$。每次递归调用时,我们需要开辟常数大小的空间存储状态变量的取值,而递归栈的深度等于树的深度,即 $O(N)$。
|
||||
|
||||
@ -0,0 +1,277 @@
|
||||
#### 方法一:使用有序映射维护区间
|
||||
|
||||
**思路与算法**
|
||||
|
||||
假设我们使用某一数据结构维护这些不相交的区间,在设计具体的数据结构之前,我们需要先明确 $\texttt{void addNum(int val)}$ 这一操作会使得当前的区间集合发生何种变化:
|
||||
|
||||
- 情况一:如果存在一个区间 $[l, r]$,它完全包含 $\textit{val}$,即 $l \leq \textit{val} \leq r$,那么在加入 $\textit{val}$ 之后,区间集合不会有任何变化;
|
||||
|
||||
- 情况二:如果存在一个区间 $[l, r]$,它的右边界 $r$「紧贴着」$\textit{val}$,即 $r + 1 = \textit{val}$,那么在加入 $\textit{val}$ 之后,该区间会从 $[l, r]$ 变为 $[l, r+1]$;
|
||||
|
||||
- 情况三:如果存在一个区间 $[l, r]$,它的左边界 $l$「紧贴着」$\textit{val}$,即 $l - 1 = \textit{val}$,那么在加入 $\textit{val}$ 之后,该区间会从 $[l, r]$ 变为 $[l - 1, r]$;
|
||||
|
||||
- 情况四:如果情况二和情况三同时满足,即存在一个区间 $[l_0, r_0]$ 满足 $r_0+1 = \textit{val}$,并且存在一个区间 $[l_1, r_1]$ 满足 $l_1-1 = \textit{val}$,那么在加入 $\textit{val}$ 之后,这两个区间会合并成一个大区间 $[l_0, r_1]$;
|
||||
|
||||
- 情况五:在上述四种情况均不满足的情况下,$\textit{val}$ 会单独形成一个新的区间 $[\textit{val}, \textit{val}]$。
|
||||
|
||||
根据上面的五种情况,我们需要找到离 $\textit{val}$ 最近的两个区间。用严谨的语言可以表述为:
|
||||
|
||||
> 对于给定的 $\textit{val}$,我们需要找到区间 $[l_0, r_0]$,使得 $l_0$ 是**最大的**满足 $l_0 \leq \textit{val}$ 的区间。同时,我们需要找到区间 $[l_1, r_1]$,使得 $l_1$ 是**最小的**满足 $l_1 > \textit{val}$ 的区间。
|
||||
|
||||
如果我们的数据结构能够快速找到这两个区间,那么上面的五种情况分别对应为:
|
||||
|
||||
- 情况一:$l_0 \leq \textit{val} \leq l_1$;
|
||||
- 情况二:$r_0 + 1 = \textit{val}$;
|
||||
- 情况三:$l_1 - 1 = \textit{val}$;
|
||||
- 情况四:$r_0 + 1 = \textit{val}$ 并且 $l_1 - 1 = \textit{val}$;
|
||||
- 情况五:上述情况均不满足。
|
||||
|
||||
一种可以找到「最近」区间的数据结构是有序映射。有序映射中的键和值分别表示区间的左边界 $l$ 和右边界 $r$。由于有序映射支持查询「最大的比某个元素小的键」以及「最小的比某个元素大的键」这两个操作,因此我们可以快速地定位区间 $[l_0, r_0]$ 和 $[l_1, r_1]$。
|
||||
|
||||
除此之外,对于 $\texttt{int[][] getIntervals()}$ 操作,我们只需要对有序映射进行遍历,将所有的键值对返回即可。
|
||||
|
||||
**细节**
|
||||
|
||||
在实际的代码编写中,需要注意 $[l_0, r_0]$ 或 $[l_1, r_1]$ 不存在的情况。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class SummaryRanges {
|
||||
private:
|
||||
map<int, int> intervals;
|
||||
|
||||
public:
|
||||
SummaryRanges() {}
|
||||
|
||||
void addNum(int val) {
|
||||
// 找到 l1 最小的且满足 l1 > val 的区间 interval1 = [l1, r1]
|
||||
// 如果不存在这样的区间,interval1 为尾迭代器
|
||||
auto interval1 = intervals.upper_bound(val);
|
||||
// 找到 l0 最大的且满足 l0 <= val 的区间 interval0 = [l0, r0]
|
||||
// 在有序集合中,interval0 就是 interval1 的前一个区间
|
||||
// 如果不存在这样的区间,interval0 为尾迭代器
|
||||
auto interval0 = (interval1 == intervals.begin() ? intervals.end() : prev(interval1));
|
||||
|
||||
if (interval0 != intervals.end() && interval0->first <= val && val <= interval0->second) {
|
||||
// 情况一
|
||||
return;
|
||||
}
|
||||
else {
|
||||
bool left_aside = (interval0 != intervals.end() && interval0->second + 1 == val);
|
||||
bool right_aside = (interval1 != intervals.end() && interval1->first - 1 == val);
|
||||
if (left_aside && right_aside) {
|
||||
// 情况四
|
||||
int left = interval0->first, right = interval1->second;
|
||||
intervals.erase(interval0);
|
||||
intervals.erase(interval1);
|
||||
intervals.emplace(left, right);
|
||||
}
|
||||
else if (left_aside) {
|
||||
// 情况二
|
||||
++interval0->second;
|
||||
}
|
||||
else if (right_aside) {
|
||||
// 情况三
|
||||
int right = interval1->second;
|
||||
intervals.erase(interval1);
|
||||
intervals.emplace(val, right);
|
||||
}
|
||||
else {
|
||||
// 情况五
|
||||
intervals.emplace(val, val);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
vector<vector<int>> getIntervals() {
|
||||
vector<vector<int>> ans;
|
||||
for (const auto& [left, right]: intervals) {
|
||||
ans.push_back({left, right});
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class SummaryRanges {
|
||||
TreeMap<Integer, Integer> intervals;
|
||||
|
||||
public SummaryRanges() {
|
||||
intervals = new TreeMap<Integer, Integer>();
|
||||
}
|
||||
|
||||
public void addNum(int val) {
|
||||
// 找到 l1 最小的且满足 l1 > val 的区间 interval1 = [l1, r1]
|
||||
// 如果不存在这样的区间,interval1 为尾迭代器
|
||||
Map.Entry<Integer, Integer> interval1 = intervals.ceilingEntry(val + 1);
|
||||
// 找到 l0 最大的且满足 l0 <= val 的区间 interval0 = [l0, r0]
|
||||
// 在有序集合中,interval0 就是 interval1 的前一个区间
|
||||
// 如果不存在这样的区间,interval0 为尾迭代器
|
||||
Map.Entry<Integer, Integer> interval0 = intervals.floorEntry(val);
|
||||
|
||||
if (interval0 != null && interval0.getKey() <= val && val <= interval0.getValue()) {
|
||||
// 情况一
|
||||
return;
|
||||
} else {
|
||||
boolean leftAside = interval0 != null && interval0.getValue() + 1 == val;
|
||||
boolean rightAside = interval1 != null && interval1.getKey() - 1 == val;
|
||||
if (leftAside && rightAside) {
|
||||
// 情况四
|
||||
int left = interval0.getKey(), right = interval1.getValue();
|
||||
intervals.remove(interval0.getKey());
|
||||
intervals.remove(interval1.getKey());
|
||||
intervals.put(left, right);
|
||||
} else if (leftAside) {
|
||||
// 情况二
|
||||
intervals.put(interval0.getKey(), interval0.getValue() + 1);
|
||||
} else if (rightAside) {
|
||||
// 情况三
|
||||
int right = interval1.getValue();
|
||||
intervals.remove(interval1.getKey());
|
||||
intervals.put(val, right);
|
||||
} else {
|
||||
// 情况五
|
||||
intervals.put(val, val);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public int[][] getIntervals() {
|
||||
int size = intervals.size();
|
||||
int[][] ans = new int[size][2];
|
||||
int index = 0;
|
||||
for (Map.Entry<Integer, Integer> entry : intervals.entrySet()) {
|
||||
int left = entry.getKey(), right = entry.getValue();
|
||||
ans[index][0] = left;
|
||||
ans[index][1] = right;
|
||||
++index;
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
from sortedcontainers import SortedDict
|
||||
|
||||
class SummaryRanges:
|
||||
|
||||
def __init__(self):
|
||||
self.intervals = SortedDict()
|
||||
|
||||
def addNum(self, val: int) -> None:
|
||||
intervals_ = self.intervals
|
||||
keys_ = self.intervals.keys()
|
||||
values_ = self.intervals.values()
|
||||
|
||||
# 找到 l1 最小的且满足 l1 > val 的区间 interval1 = [l1, r1]
|
||||
# 如果不存在这样的区间,interval1 为 len(intervals)
|
||||
interval1 = intervals_.bisect_right(val)
|
||||
# 找到 l0 最大的且满足 l0 <= val 的区间 interval0 = [l0, r0]
|
||||
# 在有序集合中,interval0 就是 interval1 的前一个区间
|
||||
# 如果不存在这样的区间,interval0 为尾迭代器
|
||||
interval0 = (len(intervals_) if interval1 == 0 else interval1 - 1)
|
||||
|
||||
if interval0 != len(intervals_) and keys_[interval0] <= val <= values_[interval0]:
|
||||
# 情况一
|
||||
return
|
||||
else:
|
||||
left_aside = (interval0 != len(intervals_) and values_[interval0] + 1 == val)
|
||||
right_aside = (interval1 != len(intervals_) and keys_[interval1] - 1 == val)
|
||||
if left_aside and right_aside:
|
||||
# 情况四
|
||||
left, right = keys_[interval0], values_[interval1]
|
||||
intervals_.popitem(interval1)
|
||||
intervals_.popitem(interval0)
|
||||
intervals_[left] = right
|
||||
elif left_aside:
|
||||
# 情况二
|
||||
intervals_[keys_[interval0]] += 1
|
||||
elif right_aside:
|
||||
# 情况三
|
||||
right = values_[interval1]
|
||||
intervals_.popitem(interval1)
|
||||
intervals_[val] = right
|
||||
else:
|
||||
# 情况五
|
||||
intervals_[val] = val
|
||||
|
||||
def getIntervals(self) -> List[List[int]]:
|
||||
# 这里实际上返回的是 List[Tuple[int, int]] 类型
|
||||
# 但 Python 的类型提示不是强制的,因此也可以通过
|
||||
return list(self.intervals.items())
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
type SummaryRanges struct {
|
||||
*redblacktree.Tree
|
||||
}
|
||||
|
||||
func Constructor() SummaryRanges {
|
||||
return SummaryRanges{redblacktree.NewWithIntComparator()}
|
||||
}
|
||||
|
||||
func (ranges *SummaryRanges) AddNum(val int) {
|
||||
// 找到 l0 最大的且满足 l0 <= val 的区间 interval0 = [l0, r0]
|
||||
interval0, has0 := ranges.Floor(val)
|
||||
if has0 && val <= interval0.Value.(int) {
|
||||
// 情况一
|
||||
return
|
||||
}
|
||||
|
||||
// 找到 l1 最小的且满足 l1 > val 的区间 interval1 = [l1, r1]
|
||||
// 在有序集合中,interval1 就是 interval0 的后一个区间
|
||||
interval1 := ranges.Iterator()
|
||||
if has0 {
|
||||
interval1 = ranges.IteratorAt(interval0)
|
||||
}
|
||||
has1 := interval1.Next()
|
||||
|
||||
leftAside := has0 && interval0.Value.(int)+1 == val
|
||||
rightAside := has1 && interval1.Key().(int)-1 == val
|
||||
if leftAside && rightAside {
|
||||
// 情况四
|
||||
interval0.Value = interval1.Value().(int)
|
||||
ranges.Remove(interval1.Key())
|
||||
} else if leftAside {
|
||||
// 情况二
|
||||
interval0.Value = val
|
||||
} else if rightAside {
|
||||
// 情况三
|
||||
right := interval1.Value().(int)
|
||||
ranges.Remove(interval1.Key())
|
||||
ranges.Put(val, right)
|
||||
} else {
|
||||
// 情况五
|
||||
ranges.Put(val, val)
|
||||
}
|
||||
}
|
||||
|
||||
func (ranges *SummaryRanges) GetIntervals() [][]int {
|
||||
ans := make([][]int, 0, ranges.Size())
|
||||
for it := ranges.Iterator(); it.Next(); {
|
||||
ans = append(ans, []int{it.Key().(int), it.Value().(int)})
|
||||
}
|
||||
return ans
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:
|
||||
|
||||
- $\texttt{void addNum(int val)}$ 的时间复杂度为 $O(\log n)$,即为对有序映射进行常数次添加、删除、修改操作需要的时间。
|
||||
|
||||
- $\texttt{int[][] getIntervals()}$ 的时间复杂度为 $O(n)$,即为对有序映射进行一次遍历需要的时间。
|
||||
- 空间复杂度:$O(n)$。在最坏情况下,数据流中的 $n$ 个元素分别独自形成一个区间,有序映射中包含 $n$ 个键值对。
|
||||
|
||||
@ -0,0 +1,381 @@
|
||||
#### 前言
|
||||
|
||||
本题是「[91. 解码方法](https://leetcode-cn.com/problems/decode-ways/)」的进阶题目。
|
||||
|
||||
#### 方法一:动态规划
|
||||
|
||||
**思路与算法**
|
||||
|
||||
对于给定的字符串 $s$,设它的长度为 $n$,其中的字符从左到右依次为 $s[1], s[2], \cdots, s[n]$。我们可以使用动态规划的方法计算出字符串 $s$ 的解码方法数。
|
||||
|
||||
具体地,设 $f_i$ 表示字符串 $s$ 的前 $i$ 个字符 $s[1..i]$ 的解码方法数。在进行状态转移时,我们可以考虑最后一次解码使用了 $s$ 中的哪些字符,那么会有下面的两种情况:
|
||||
|
||||
- 第一种情况是我们使用了一个字符,即 $s[i]$ 进行解码,那么:
|
||||
|
||||
- 如果 $s[i]$ 为 $*$,那么它对应着 $[1, 9]$ 中的任意一种编码,有 $9$ 种方案。因此状态转移方程为:
|
||||
|
||||
$$
|
||||
f_i = 9 \times f_
|
||||
$$
|
||||
|
||||
- 如果 $s[i]$ 为 $0$,那么它无法被解码。因此状态转移方程为:
|
||||
|
||||
$$
|
||||
f_i = 0
|
||||
$$
|
||||
|
||||
- 对于其它的情况,$s[i] \in [1, 9]$,分别对应一种编码。因此状态转移方程为:
|
||||
|
||||
$$
|
||||
f_i = f_
|
||||
$$
|
||||
|
||||
- 第二种情况是我们使用了两个字符,即 $s[i-1]$ 和 $s[i]$ 进行编码。与第一种情况类似,我们需要进行分类讨论:
|
||||
- 如果 $s[i-1]$ 和 $s[i]$ 均为 $*$,那么它们对应着 $[11,19]$ 以及 $[21, 26]$ 中的任意一种编码,有 $15$ 种方案。因此状态转移方程为:
|
||||
|
||||
$$
|
||||
f_i = 15 \times f_
|
||||
$$
|
||||
|
||||
- 如果仅有 $s[i-1]$ 为 $*$,那么当 $s[i] \in [0, 6]$ 时,$s[i-1]$ 可以选择 $1$ 和 $2$;当 $s[i] \in [7, 9]$ 时,$s[i-1]$ 只能选择 $1$。因此状态转移方程为:
|
||||
|
||||
$$
|
||||
f_i = \begin
|
||||
2 \times f_, & \quad s[i-1] \in [1, 6] \\
|
||||
f_, & \quad s[i-1] \in [7, 9]
|
||||
\end
|
||||
$$
|
||||
|
||||
- 如果仅有 $s[i]$ 为 $*$,那么当 $s[i-1]$ 为 $1$ 时,$s[i]$ 可以在 $[1, 9]$ 中进行选择;当 $s[i-1]$ 为 $2$ 时,$s[i]$ 可以在 $[1, 6]$ 中进行选择;对于其余情况,它们无法被解码。因此状态转移方程为:
|
||||
|
||||
$$
|
||||
f_i = \begin
|
||||
9 \times f_, & \quad s[i] = 1 \\
|
||||
6 \times f_, & \quad s[i] = 2 \\
|
||||
0, & \quad \text
|
||||
\end
|
||||
$$
|
||||
|
||||
- 如果 $s[i-1]$ 和 $s[i]$ 均不为 $*$,那么只有 $s[i-1]$ 不为 $0$ 并且 $s[i-1]$ 和 $s[i]$ 组成的数字小于等于 $26$ 时,它们才能被解码。因此状态转移方程为:
|
||||
|
||||
$$
|
||||
f_i = \begin
|
||||
f_, & \quad s[i-1] \neq 0 \wedge \overline{s[i-1]s[i]} \leq 26 \\
|
||||
0, & \quad \text
|
||||
\end
|
||||
$$
|
||||
|
||||
将上面的两种状态转移方程在对应的条件满足时进行累加,即可得到 $f_i$ 的值。在动态规划完成后,最终的答案即为 $f_n$。
|
||||
|
||||
**细节**
|
||||
|
||||
动态规划的边界条件为:
|
||||
|
||||
$$
|
||||
f_0 = 1
|
||||
$$
|
||||
|
||||
即**空字符串可以有 $1$ 种解码方法,解码出一个空字符串**。
|
||||
|
||||
同时,由于在大部分语言中,字符串的下标是从 $0$ 而不是 $1$ 开始的,因此在代码的编写过程中,我们需要将所有字符串的下标减去 $1$,与使用的语言保持一致。
|
||||
|
||||
最终的状态转移方程可以写成:
|
||||
|
||||
$$
|
||||
f_i = \alpha \times f_ + \beta \times f_
|
||||
$$
|
||||
|
||||
的形式。为了使得代码更加易读,我们可以使用两个辅助函数,给定对应的一个或两个字符,分别计算出 $\alpha$ 和 $\beta$ 的值。
|
||||
|
||||
注意到在状态转移方程中,$f_i$ 的值仅与 $f_{i-1}$ 和 $f_{i-2}$ 有关,因此我们可以使用三个变量进行状态转移,省去数组的空间。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
static constexpr int mod = 1000000007;
|
||||
|
||||
public:
|
||||
int numDecodings(string s) {
|
||||
auto check1digit = [](char ch) -> int {
|
||||
if (ch == '0') {
|
||||
return 0;
|
||||
}
|
||||
return ch == '*' ? 9 : 1;
|
||||
};
|
||||
|
||||
auto check2digits = [](char c0, char c1) -> int {
|
||||
if (c0 == '*' && c1 == '*') {
|
||||
return 15;
|
||||
}
|
||||
if (c0 == '*') {
|
||||
return c1 <= '6' ? 2 : 1;
|
||||
}
|
||||
if (c1 == '*') {
|
||||
if (c0 == '1') {
|
||||
return 9;
|
||||
}
|
||||
if (c0 == '2') {
|
||||
return 6;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
return c0 != '0' && (c0 - '0') * 10 + (c1 - '0') <= 26;
|
||||
};
|
||||
|
||||
int n = s.size();
|
||||
// a = f[i-2], b = f[i-1], c = f[i]
|
||||
int a = 0, b = 1, c = 0;
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
c = (long long)b * check1digit(s[i - 1]) % mod;
|
||||
if (i > 1) {
|
||||
c = (c + (long long)a * check2digits(s[i - 2], s[i - 1])) % mod;
|
||||
}
|
||||
a = b;
|
||||
b = c;
|
||||
}
|
||||
return c;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
static final int MOD = 1000000007;
|
||||
|
||||
public int numDecodings(String s) {
|
||||
int n = s.length();
|
||||
// a = f[i-2], b = f[i-1], c = f[i]
|
||||
long a = 0, b = 1, c = 0;
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
c = b * check1digit(s.charAt(i - 1)) % MOD;
|
||||
if (i > 1) {
|
||||
c = (c + a * check2digits(s.charAt(i - 2), s.charAt(i - 1))) % MOD;
|
||||
}
|
||||
a = b;
|
||||
b = c;
|
||||
}
|
||||
return (int) c;
|
||||
}
|
||||
|
||||
public int check1digit(char ch) {
|
||||
if (ch == '0') {
|
||||
return 0;
|
||||
}
|
||||
return ch == '*' ? 9 : 1;
|
||||
}
|
||||
|
||||
public int check2digits(char c0, char c1) {
|
||||
if (c0 == '*' && c1 == '*') {
|
||||
return 15;
|
||||
}
|
||||
if (c0 == '*') {
|
||||
return c1 <= '6' ? 2 : 1;
|
||||
}
|
||||
if (c1 == '*') {
|
||||
if (c0 == '1') {
|
||||
return 9;
|
||||
}
|
||||
if (c0 == '2') {
|
||||
return 6;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
return (c0 != '0' && (c0 - '0') * 10 + (c1 - '0') <= 26) ? 1 : 0;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
const int MOD = 1000000007;
|
||||
|
||||
public int NumDecodings(string s) {
|
||||
int n = s.Length;
|
||||
// a = f[i-2], b = f[i-1], c = f[i]
|
||||
long a = 0, b = 1, c = 0;
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
c = b * Check1digit(s[i - 1]) % MOD;
|
||||
if (i > 1) {
|
||||
c = (c + a * Check2digits(s[i - 2], s[i - 1])) % MOD;
|
||||
}
|
||||
a = b;
|
||||
b = c;
|
||||
}
|
||||
return (int) c;
|
||||
}
|
||||
|
||||
public int Check1digit(char ch) {
|
||||
if (ch == '0') {
|
||||
return 0;
|
||||
}
|
||||
return ch == '*' ? 9 : 1;
|
||||
}
|
||||
|
||||
public int Check2digits(char c0, char c1) {
|
||||
if (c0 == '*' && c1 == '*') {
|
||||
return 15;
|
||||
}
|
||||
if (c0 == '*') {
|
||||
return c1 <= '6' ? 2 : 1;
|
||||
}
|
||||
if (c1 == '*') {
|
||||
if (c0 == '1') {
|
||||
return 9;
|
||||
}
|
||||
if (c0 == '2') {
|
||||
return 6;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
return (c0 != '0' && (c0 - '0') * 10 + (c1 - '0') <= 26) ? 1 : 0;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def numDecodings(self, s: str) -> int:
|
||||
mod = 10**9 + 7
|
||||
|
||||
def check1digit(ch: str) -> int:
|
||||
if ch == "0":
|
||||
return 0
|
||||
return 9 if ch == "*" else 1
|
||||
|
||||
def check2digits(c0: str, c1: str) -> int:
|
||||
if c0 == c1 == "*":
|
||||
return 15
|
||||
if c0 == "*":
|
||||
return 2 if c1 <= "6" else 1
|
||||
if c1 == "*":
|
||||
return 9 if c0 == "1" else (6 if c0 == "2" else 0)
|
||||
return int(c0 != "0" and int(c0) * 10 + int(c1) <= 26)
|
||||
|
||||
n = len(s)
|
||||
# a = f[i-2], b = f[i-1], c = f[i]
|
||||
a, b, c = 0, 1, 0
|
||||
for i in range(1, n + 1):
|
||||
c = b * check1digit(s[i - 1])
|
||||
if i > 1:
|
||||
c += a * check2digits(s[i - 2], s[i - 1])
|
||||
c %= mod
|
||||
a = b
|
||||
b = c
|
||||
|
||||
return c
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var numDecodings = function(s) {
|
||||
const MOD = 1000000007;
|
||||
const n = s.length;
|
||||
// a = f[i-2], b = f[i-1], c = f[i]
|
||||
let a = 0, b = 1, c = 0;
|
||||
for (let i = 1; i <= n; ++i) {
|
||||
c = b * check1digit(s[i - 1]) % MOD;
|
||||
if (i > 1) {
|
||||
c = (c + a * check2digits(s[i - 2], s[i - 1])) % MOD;
|
||||
}
|
||||
a = b;
|
||||
b = c;
|
||||
}
|
||||
return c;
|
||||
}
|
||||
|
||||
const check1digit = (ch) => {
|
||||
if (ch === '0') {
|
||||
return 0;
|
||||
}
|
||||
return ch === '*' ? 9 : 1;
|
||||
}
|
||||
|
||||
const check2digits = (c0, c1) => {
|
||||
if (c0 === '*' && c1 === '*') {
|
||||
return 15;
|
||||
}
|
||||
if (c0 === '*') {
|
||||
return c1.charCodeAt() <= '6'.charCodeAt() ? 2 : 1;
|
||||
}
|
||||
if (c1 === '*') {
|
||||
if (c0 === '1') {
|
||||
return 9;
|
||||
}
|
||||
if (c0 === '2') {
|
||||
return 6;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
return (c0 !== '0' && (c0.charCodeAt() - '0'.charCodeAt()) * 10 + (c1.charCodeAt() - '0'.charCodeAt()) <= 26) ? 1 : 0;
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func check1digit(ch byte) int {
|
||||
if ch == '*' {
|
||||
return 9
|
||||
}
|
||||
if ch == '0' {
|
||||
return 0
|
||||
}
|
||||
return 1
|
||||
}
|
||||
|
||||
func check2digits(c0, c1 byte) int {
|
||||
if c0 == '*' && c1 == '*' {
|
||||
return 15
|
||||
}
|
||||
if c0 == '*' {
|
||||
if c1 <= '6' {
|
||||
return 2
|
||||
}
|
||||
return 1
|
||||
}
|
||||
if c1 == '*' {
|
||||
if c0 == '1' {
|
||||
return 9
|
||||
}
|
||||
if c0 == '2' {
|
||||
return 6
|
||||
}
|
||||
return 0
|
||||
}
|
||||
if c0 != '0' && (c0-'0')*10+(c1-'0') <= 26 {
|
||||
return 1
|
||||
}
|
||||
return 0
|
||||
}
|
||||
|
||||
func numDecodings(s string) int {
|
||||
const mod int = 1e9 + 7
|
||||
a, b, c := 0, 1, 0
|
||||
for i := range s {
|
||||
c = b * check1digit(s[i]) % mod
|
||||
if i > 0 {
|
||||
c = (c + a*check2digits(s[i-1], s[i])) % mod
|
||||
}
|
||||
a, b = b, c
|
||||
}
|
||||
return c
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n)$,其中 $n$ 是字符串 $s$ 的长度。
|
||||
|
||||
- 空间复杂度:$O(1)$。
|
||||
|
||||
@ -0,0 +1,26 @@
|
||||
抽象固定寻找维护
|
||||
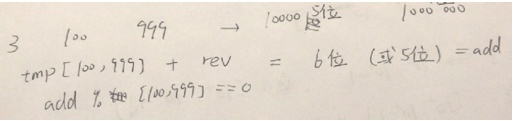
|
||||
|
||||
*
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
int largestPalindrome(int n) {
|
||||
if(n==1)return 9;
|
||||
int down=pow(10,n-1);
|
||||
int up=pow(10,n)-1;
|
||||
for(int i=up;i>=down;i--){
|
||||
string tmp=to_string(i);
|
||||
string rev(tmp.rbegin(),tmp.rend());
|
||||
string add=tmp+rev;
|
||||
long long addNum=stoll(add);
|
||||
for(long long j=up;j*j>=addNum;j--){
|
||||
if(addNum%j==0)return addNum%1337;
|
||||
}
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
@ -0,0 +1,114 @@
|
||||
#### 方法一:计算重叠面积
|
||||
|
||||
两个矩形覆盖的总面积等于两个矩形的面积之和减去两个矩形的重叠部分的面积。由于两个矩形的左下顶点和右上顶点已知,因此两个矩形的面积可以直接计算。如果两个矩形重叠,则两个矩形的重叠部分也是矩形,重叠部分的面积可以根据重叠部分的边界计算。
|
||||
|
||||
两个矩形的水平边投影到 $x$ 轴上的线段分别为 $[\textit{ax}_1, \textit{ax}_2]$ 和 $[\textit{bx}_1, \textit{bx}_2]$,竖直边投影到 $y$ 轴上的线段分别为 $[\textit{ay}_1, \textit{ay}_2]$ 和 $[\textit{by}_1, \textit{by}_2]$。如果两个矩形重叠,则重叠部分的水平边投影到 $x$ 轴上的线段为 $[\max(\textit{ax}_1, \textit{bx}_1), \min(\textit{ax}_2, \textit{bx}_2)]$,竖直边投影到 $y$ 轴上的线段为 $[\max(\textit{ay}_1, \textit{by}_1), \min(\textit{ay}_2, \textit{by}_2)]$,根据重叠部分的水平边投影到 $x$ 轴上的线段长度和竖直边投影到 $y$ 轴上的线段长度即可计算重叠部分的面积。只有当两条线段的长度都大于 $0$ 时,重叠部分的面积才大于 $0$,否则重叠部分的面积为 $0$。
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
|
||||
int area1 = (ax2 - ax1) * (ay2 - ay1), area2 = (bx2 - bx1) * (by2 - by1);
|
||||
int overlapWidth = Math.min(ax2, bx2) - Math.max(ax1, bx1), overlapHeight = Math.min(ay2, by2) - Math.max(ay1, by1);
|
||||
int overlapArea = Math.max(overlapWidth, 0) * Math.max(overlapHeight, 0);
|
||||
return area1 + area2 - overlapArea;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
public int ComputeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
|
||||
int area1 = (ax2 - ax1) * (ay2 - ay1), area2 = (bx2 - bx1) * (by2 - by1);
|
||||
int overlapWidth = Math.Min(ax2, bx2) - Math.Max(ax1, bx1), overlapHeight = Math.Min(ay2, by2) - Math.Max(ay1, by1);
|
||||
int overlapArea = Math.Max(overlapWidth, 0) * Math.Max(overlapHeight, 0);
|
||||
return area1 + area2 - overlapArea;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
|
||||
int area1 = (ax2 - ax1) * (ay2 - ay1), area2 = (bx2 - bx1) * (by2 - by1);
|
||||
int overlapWidth = min(ax2, bx2) - max(ax1, bx1), overlapHeight = min(ay2, by2) - max(ay1, by1);
|
||||
int overlapArea = max(overlapWidth, 0) * max(overlapHeight, 0);
|
||||
return area1 + area2 - overlapArea;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var computeArea = function(ax1, ay1, ax2, ay2, bx1, by1, bx2, by2) {
|
||||
const area1 = (ax2 - ax1) * (ay2 - ay1), area2 = (bx2 - bx1) * (by2 - by1);
|
||||
const overlapWidth = Math.min(ax2, bx2) - Math.max(ax1, bx1), overlapHeight = Math.min(ay2, by2) - Math.max(ay1, by1);
|
||||
const overlapArea = Math.max(overlapWidth, 0) * Math.max(overlapHeight, 0);
|
||||
return area1 + area2 - overlapArea;
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
|
||||
int area1 = (ax2 - ax1) * (ay2 - ay1), area2 = (bx2 - bx1) * (by2 - by1);
|
||||
int overlapWidth = fmin(ax2, bx2) - fmax(ax1, bx1), overlapHeight = fmin(ay2, by2) - fmax(ay1, by1);
|
||||
int overlapArea = fmax(overlapWidth, 0) * fmax(overlapHeight, 0);
|
||||
return area1 + area2 - overlapArea;
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func computeArea(ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 int) int {
|
||||
area1 := (ax2 - ax1) * (ay2 - ay1)
|
||||
area2 := (bx2 - bx1) * (by2 - by1)
|
||||
overlapWidth := min(ax2, bx2) - max(ax1, bx1)
|
||||
overlapHeight := min(ay2, by2) - max(ay1, by1)
|
||||
overlapArea := max(overlapWidth, 0) * max(overlapHeight, 0)
|
||||
return area1 + area2 - overlapArea
|
||||
}
|
||||
|
||||
func min(a, b int) int {
|
||||
if a > b {
|
||||
return b
|
||||
}
|
||||
return a
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if b > a {
|
||||
return b
|
||||
}
|
||||
return a
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def computeArea(self, ax1: int, ay1: int, ax2: int, ay2: int, bx1: int, by1: int, bx2: int, by2: int) -> int:
|
||||
area1 = (ax2 - ax1) * (ay2 - ay1)
|
||||
area2 = (bx2 - bx1) * (by2 - by1)
|
||||
overlapWidth = min(ax2, bx2) - max(ax1, bx1)
|
||||
overlapHeight = min(ay2, by2) - max(ay1, by1)
|
||||
overlapArea = max(overlapWidth, 0) * max(overlapHeight, 0)
|
||||
return area1 + area2 - overlapArea
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(1)$。
|
||||
|
||||
- 空间复杂度:$O(1)$。
|
||||
|
||||
@ -0,0 +1,630 @@
|
||||
### 📺 视频题解
|
||||
|
||||

|
||||
|
||||
### 📖 文字题解
|
||||
|
||||
#### 前言
|
||||
|
||||
由于题目规定了「只能存储 $32$ 位整数」,本题解的正文部分和代码中都不会使用任何 $64$ 位整数。**诚然,使用 $64$ 位整数可以极大地方便我们的编码,但这是违反题目规则的。**
|
||||
|
||||
如果除法结果溢出,那么我们需要返回 $2^{31} - 1$ 作为答案。因此在编码之前,我们可以首先对于溢出或者容易出错的边界情况进行讨论:
|
||||
|
||||
- 当被除数为 $32$ 位有符号整数的最小值 $-2^{31}$ 时:
|
||||
|
||||
- 如果除数为 $1$,那么我们可以直接返回答案 $-2^{31}$;
|
||||
- 如果除数为 $-1$,那么答案为 $2^{31}$,产生了溢出。此时我们需要返回 $2^{31} - 1$。
|
||||
- 当除数为 $32$ 位有符号整数的最小值 $-2^{31}$ 时:
|
||||
|
||||
- 如果被除数同样为 $-2^{31}$,那么我们可以直接返回答案 $1$;
|
||||
- 对于其余的情况,我们返回答案 $0$。
|
||||
- 当被除数为 $0$ 时,我们可以直接返回答案 $0$。
|
||||
|
||||
对于一般的情况,根据除数和被除数的符号,我们需要考虑 $4$ 种不同的可能性。因此,为了方便编码,我们可以将被除数或者除数取相反数,使得它们符号相同。
|
||||
|
||||
如果我们将被除数和除数都变为正数,那么可能会导致溢出。例如当被除数为 $-2^{31}$ 时,它的相反数 $2^{31}$ 产生了溢出。因此,我们可以考虑将被除数和除数都变为负数,这样就不会有溢出的问题,在编码时只需要考虑 $1$ 种情况了。
|
||||
|
||||
如果我们将被除数和除数的其中(恰好)一个变为了正数,那么在返回答案之前,我们需要对答案也取相反数。
|
||||
|
||||
#### 方法一:二分查找
|
||||
|
||||
**思路与算法**
|
||||
|
||||
根据「前言」部分的讨论,我们记被除数为 $X$,除数为 $Y$,并且 $X$ 和 $Y$ 都是负数。我们需要找出 $X/Y$ 的结果 $Z$。$Z$ 一定是正数或 $0$。
|
||||
|
||||
根据除法以及余数的定义,我们可以将其改成乘法的等价形式,即:
|
||||
|
||||
$$
|
||||
Z \times Y \geq X > (Z+1) \times Y
|
||||
$$
|
||||
|
||||
因此,我们可以使用二分查找的方法得到 $Z$,即找出**最大**的 $Z$ 使得 $Z \times Y \geq X$ 成立。
|
||||
|
||||
由于我们不能使用乘法运算符,因此我们需要使用「快速乘」算法得到 $Z \times Y$ 的值。「快速乘」算法与「快速幂」类似,前者通过加法实现乘法,后者通过乘法实现幂运算。「快速幂」算法可以参考[「50. Pow(x, n)」的官方题解](https://leetcode-cn.com/problems/powx-n/solution/powx-n-by-leetcode-solution/),「快速乘」算法只需要在「快速幂」算法的基础上,将乘法运算改成加法运算即可。
|
||||
|
||||
**细节**
|
||||
|
||||
由于我们只能使用 $32$ 位整数,因此二分查找中会有很多细节。
|
||||
|
||||
首先,二分查找的下界为 $1$,上界为 $2^{31} - 1$。唯一可能出现的答案为 $2^{31}$ 的情况已经被我们在「前言」部分进行了特殊处理,因此答案的最大值为 $2^{31} - 1$。如果二分查找失败,那么答案一定为 $0$。
|
||||
|
||||
在实现「快速乘」时,我们需要使用加法运算,然而较大的 $Z$ 也会导致加法运算溢出。例如我们要判断 $A + B$ 是否小于 $C$ 时(其中 $A, B, C$ 均为负数),$A + B$ 可能会产生溢出,因此我们必须将判断改为 $A < C - B$ 是否成立。由于任意两个负数的差一定在 $[-2^{31} + 1, 2^{31} - 1]$ 范围内,这样就不会产生溢出。
|
||||
|
||||
读者可以阅读下面的代码和注释,理解如何避免使用乘法和出发,以及正确处理溢出问题。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int divide(int dividend, int divisor) {
|
||||
// 考虑被除数为最小值的情况
|
||||
if (dividend == INT_MIN) {
|
||||
if (divisor == 1) {
|
||||
return INT_MIN;
|
||||
}
|
||||
if (divisor == -1) {
|
||||
return INT_MAX;
|
||||
}
|
||||
}
|
||||
// 考虑除数为最小值的情况
|
||||
if (divisor == INT_MIN) {
|
||||
return dividend == INT_MIN ? 1 : 0;
|
||||
}
|
||||
// 考虑被除数为 0 的情况
|
||||
if (dividend == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
// 一般情况,使用二分查找
|
||||
// 将所有的正数取相反数,这样就只需要考虑一种情况
|
||||
bool rev = false;
|
||||
if (dividend > 0) {
|
||||
dividend = -dividend;
|
||||
rev = !rev;
|
||||
}
|
||||
if (divisor > 0) {
|
||||
divisor = -divisor;
|
||||
rev = !rev;
|
||||
}
|
||||
|
||||
// 快速乘
|
||||
auto quickAdd = [](int y, int z, int x) {
|
||||
// x 和 y 是负数,z 是正数
|
||||
// 需要判断 z * y >= x 是否成立
|
||||
int result = 0, add = y;
|
||||
while (z) {
|
||||
if (z & 1) {
|
||||
// 需要保证 result + add >= x
|
||||
if (result < x - add) {
|
||||
return false;
|
||||
}
|
||||
result += add;
|
||||
}
|
||||
if (z != 1) {
|
||||
// 需要保证 add + add >= x
|
||||
if (add < x - add) {
|
||||
return false;
|
||||
}
|
||||
add += add;
|
||||
}
|
||||
// 不能使用除法
|
||||
z >>= 1;
|
||||
}
|
||||
return true;
|
||||
};
|
||||
|
||||
int left = 1, right = INT_MAX, ans = 0;
|
||||
while (left <= right) {
|
||||
// 注意溢出,并且不能使用除法
|
||||
int mid = left + ((right - left) >> 1);
|
||||
bool check = quickAdd(divisor, mid, dividend);
|
||||
if (check) {
|
||||
ans = mid;
|
||||
// 注意溢出
|
||||
if (mid == INT_MAX) {
|
||||
break;
|
||||
}
|
||||
left = mid + 1;
|
||||
}
|
||||
else {
|
||||
right = mid - 1;
|
||||
}
|
||||
}
|
||||
|
||||
return rev ? -ans : ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int divide(int dividend, int divisor) {
|
||||
// 考虑被除数为最小值的情况
|
||||
if (dividend == Integer.MIN_VALUE) {
|
||||
if (divisor == 1) {
|
||||
return Integer.MIN_VALUE;
|
||||
}
|
||||
if (divisor == -1) {
|
||||
return Integer.MAX_VALUE;
|
||||
}
|
||||
}
|
||||
// 考虑除数为最小值的情况
|
||||
if (divisor == Integer.MIN_VALUE) {
|
||||
return dividend == Integer.MIN_VALUE ? 1 : 0;
|
||||
}
|
||||
// 考虑被除数为 0 的情况
|
||||
if (dividend == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
// 一般情况,使用二分查找
|
||||
// 将所有的正数取相反数,这样就只需要考虑一种情况
|
||||
boolean rev = false;
|
||||
if (dividend > 0) {
|
||||
dividend = -dividend;
|
||||
rev = !rev;
|
||||
}
|
||||
if (divisor > 0) {
|
||||
divisor = -divisor;
|
||||
rev = !rev;
|
||||
}
|
||||
|
||||
int left = 1, right = Integer.MAX_VALUE, ans = 0;
|
||||
while (left <= right) {
|
||||
// 注意溢出,并且不能使用除法
|
||||
int mid = left + ((right - left) >> 1);
|
||||
boolean check = quickAdd(divisor, mid, dividend);
|
||||
if (check) {
|
||||
ans = mid;
|
||||
// 注意溢出
|
||||
if (mid == Integer.MAX_VALUE) {
|
||||
break;
|
||||
}
|
||||
left = mid + 1;
|
||||
} else {
|
||||
right = mid - 1;
|
||||
}
|
||||
}
|
||||
|
||||
return rev ? -ans : ans;
|
||||
}
|
||||
|
||||
// 快速乘
|
||||
public boolean quickAdd(int y, int z, int x) {
|
||||
// x 和 y 是负数,z 是正数
|
||||
// 需要判断 z * y >= x 是否成立
|
||||
int result = 0, add = y;
|
||||
while (z != 0) {
|
||||
if ((z & 1) != 0) {
|
||||
// 需要保证 result + add >= x
|
||||
if (result < x - add) {
|
||||
return false;
|
||||
}
|
||||
result += add;
|
||||
}
|
||||
if (z != 1) {
|
||||
// 需要保证 add + add >= x
|
||||
if (add < x - add) {
|
||||
return false;
|
||||
}
|
||||
add += add;
|
||||
}
|
||||
// 不能使用除法
|
||||
z >>= 1;
|
||||
}
|
||||
return true;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
public int Divide(int dividend, int divisor) {
|
||||
// 考虑被除数为最小值的情况
|
||||
if (dividend == int.MinValue) {
|
||||
if (divisor == 1) {
|
||||
return int.MinValue;
|
||||
}
|
||||
if (divisor == -1) {
|
||||
return int.MaxValue;
|
||||
}
|
||||
}
|
||||
// 考虑除数为最小值的情况
|
||||
if (divisor == int.MinValue) {
|
||||
return dividend == int.MinValue ? 1 : 0;
|
||||
}
|
||||
// 考虑被除数为 0 的情况
|
||||
if (dividend == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
// 一般情况,使用二分查找
|
||||
// 将所有的正数取相反数,这样就只需要考虑一种情况
|
||||
bool rev = false;
|
||||
if (dividend > 0) {
|
||||
dividend = -dividend;
|
||||
rev = !rev;
|
||||
}
|
||||
if (divisor > 0) {
|
||||
divisor = -divisor;
|
||||
rev = !rev;
|
||||
}
|
||||
|
||||
int left = 1, right = int.MaxValue, ans = 0;
|
||||
while (left <= right) {
|
||||
// 注意溢出,并且不能使用除法
|
||||
int mid = left + ((right - left) >> 1);
|
||||
bool check = quickAdd(divisor, mid, dividend);
|
||||
if (check) {
|
||||
ans = mid;
|
||||
// 注意溢出
|
||||
if (mid == int.MaxValue) {
|
||||
break;
|
||||
}
|
||||
left = mid + 1;
|
||||
} else {
|
||||
right = mid - 1;
|
||||
}
|
||||
}
|
||||
|
||||
return rev ? -ans : ans;
|
||||
}
|
||||
|
||||
// 快速乘
|
||||
public bool quickAdd(int y, int z, int x) {
|
||||
// x 和 y 是负数,z 是正数
|
||||
// 需要判断 z * y >= x 是否成立
|
||||
int result = 0, add = y;
|
||||
while (z != 0) {
|
||||
if ((z & 1) != 0) {
|
||||
// 需要保证 result + add >= x
|
||||
if (result < x - add) {
|
||||
return false;
|
||||
}
|
||||
result += add;
|
||||
}
|
||||
if (z != 1) {
|
||||
// 需要保证 add + add >= x
|
||||
if (add < x - add) {
|
||||
return false;
|
||||
}
|
||||
add += add;
|
||||
}
|
||||
// 不能使用除法
|
||||
z >>= 1;
|
||||
}
|
||||
return true;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def divide(self, dividend: int, divisor: int) -> int:
|
||||
INT_MIN, INT_MAX = -2**31, 2**31 - 1
|
||||
|
||||
# 考虑被除数为最小值的情况
|
||||
if dividend == INT_MIN:
|
||||
if divisor == 1:
|
||||
return INT_MIN
|
||||
if divisor == -1:
|
||||
return INT_MAX
|
||||
|
||||
# 考虑除数为最小值的情况
|
||||
if divisor == INT_MIN:
|
||||
return 1 if dividend == INT_MIN else 0
|
||||
# 考虑被除数为 0 的情况
|
||||
if dividend == 0:
|
||||
return 0
|
||||
|
||||
# 一般情况,使用二分查找
|
||||
# 将所有的正数取相反数,这样就只需要考虑一种情况
|
||||
rev = False
|
||||
if dividend > 0:
|
||||
dividend = -dividend
|
||||
rev = not rev
|
||||
if divisor > 0:
|
||||
divisor = -divisor
|
||||
rev = not rev
|
||||
|
||||
# 快速乘
|
||||
def quickAdd(y: int, z: int, x: int) -> bool:
|
||||
# x 和 y 是负数,z 是正数
|
||||
# 需要判断 z * y >= x 是否成立
|
||||
result, add = 0, y
|
||||
while z > 0:
|
||||
if (z & 1) == 1:
|
||||
# 需要保证 result + add >= x
|
||||
if result < x - add:
|
||||
return False
|
||||
result += add
|
||||
if z != 1:
|
||||
# 需要保证 add + add >= x
|
||||
if add < x - add:
|
||||
return False
|
||||
add += add
|
||||
# 不能使用除法
|
||||
z >>= 1
|
||||
return True
|
||||
|
||||
left, right, ans = 1, INT_MAX, 0
|
||||
while left <= right:
|
||||
# 注意溢出,并且不能使用除法
|
||||
mid = left + ((right - left) >> 1)
|
||||
check = quickAdd(divisor, mid, dividend)
|
||||
if check:
|
||||
ans = mid
|
||||
# 注意溢出
|
||||
if mid == INT_MAX:
|
||||
break
|
||||
left = mid + 1
|
||||
else:
|
||||
right = mid - 1
|
||||
|
||||
return -ans if rev else ans
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(\log^2 C)$,其中 $C$ 表示 $32$ 位整数的范围。二分查找的次数为 $O(\log C)$,其中的每一步我们都需要 $O(\log C)$ 使用「快速乘」算法判断 $Z \times Y \geq X$ 是否成立,因此总时间复杂度为 $O(\log^2 C)$。
|
||||
|
||||
- 空间复杂度:$O(1)$。
|
||||
|
||||
#### 方法二:类二分查找
|
||||
|
||||
**前言**
|
||||
|
||||
常规意义下的二分查找为:给定区间 $[l, r]$,取该区间的中点 $\textit{mid} = \lfloor \dfrac{l+r}{2} \rfloor$,根据 $\textit{mid}$ 处是否满足某一条件,来决定移动左边界 $l$ 还是右边界 $r$。
|
||||
|
||||
我们也可以考虑另一种二分查找的方法:
|
||||
|
||||
- 记 $k$ 为满足 $2^k \leq r-l < 2^{k+1}$ 的 $k$ 值。
|
||||
|
||||
- 二分查找会进行 $k+1$ 次。在第 $i ~ (1 \leq i \leq k+1)$ 次二分查找时,设区间为 $[l_i, r_i]$,我们取 $\textit{mid} = l_i + 2^{k+1-i}$:
|
||||
|
||||
- 如果 $\textit{mid}$ 不在 $[l_i, r_i]$ 的范围内,那么我们直接忽略这次二分查找;
|
||||
|
||||
- 如果 $\textit{mid}$ 在 $[l_i, r_i]$ 的范围内,并且 $\textit{mid}$ 处满足某一条件,我们就将 $l_i$ 更新为 $\textit{mid}$,否则同样忽略这次二分查找。
|
||||
|
||||
最终 $l_i$ 即为二分查找的结果。这样做的正确性在于:
|
||||
|
||||
> 设在常规意义下的二分查找的答案为 $\textit{ans}$,记 $\delta$ 为 $\textit{ans}$ 与左边界的差值 $\textit{ans} - l$。$\delta$ 不会大于 $r-l$,并且 $\delta$ 一定可以用 $2^k, 2^{k-1}, 2^{k-2}, \cdots, 2^1, 2^0$ 中的若干个元素之和表示(考虑 $\delta$ 的二进制表示的意义即可)。因此上述二分查找是正确的。
|
||||
|
||||
**思路与算法**
|
||||
|
||||
基于上述的二分查找的方法,我们可以设计出如下的算法:
|
||||
|
||||
- 我们首先不断地将 $Y$ 乘以 $2$(通过加法运算实现),并将这些结果放入数组中,其中数组的第 $i$ 项就等于 $Y \times 2^i$。这一过程直到 $Y$ 的两倍严格小于 $X$ 为止。
|
||||
|
||||
- 我们对数组进行逆序遍历。当遍历到第 $i$ 项时,如果其大于等于 $X$,我们就将答案增加 $2^i$,并且将 $X$ 中减去这一项的值。
|
||||
|
||||
本质上,上述的逆序遍历就模拟了二分查找的过程。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol2-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int divide(int dividend, int divisor) {
|
||||
// 考虑被除数为最小值的情况
|
||||
if (dividend == INT_MIN) {
|
||||
if (divisor == 1) {
|
||||
return INT_MIN;
|
||||
}
|
||||
if (divisor == -1) {
|
||||
return INT_MAX;
|
||||
}
|
||||
}
|
||||
// 考虑除数为最小值的情况
|
||||
if (divisor == INT_MIN) {
|
||||
return dividend == INT_MIN ? 1 : 0;
|
||||
}
|
||||
// 考虑被除数为 0 的情况
|
||||
if (dividend == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
// 一般情况,使用类二分查找
|
||||
// 将所有的正数取相反数,这样就只需要考虑一种情况
|
||||
bool rev = false;
|
||||
if (dividend > 0) {
|
||||
dividend = -dividend;
|
||||
rev = !rev;
|
||||
}
|
||||
if (divisor > 0) {
|
||||
divisor = -divisor;
|
||||
rev = !rev;
|
||||
}
|
||||
|
||||
vector<int> candidates = {divisor};
|
||||
// 注意溢出
|
||||
while (candidates.back() >= dividend - candidates.back()) {
|
||||
candidates.push_back(candidates.back() + candidates.back());
|
||||
}
|
||||
int ans = 0;
|
||||
for (int i = candidates.size() - 1; i >= 0; --i) {
|
||||
if (candidates[i] >= dividend) {
|
||||
ans += (1 << i);
|
||||
dividend -= candidates[i];
|
||||
}
|
||||
}
|
||||
|
||||
return rev ? -ans : ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int divide(int dividend, int divisor) {
|
||||
// 考虑被除数为最小值的情况
|
||||
if (dividend == Integer.MIN_VALUE) {
|
||||
if (divisor == 1) {
|
||||
return Integer.MIN_VALUE;
|
||||
}
|
||||
if (divisor == -1) {
|
||||
return Integer.MAX_VALUE;
|
||||
}
|
||||
}
|
||||
// 考虑除数为最小值的情况
|
||||
if (divisor == Integer.MIN_VALUE) {
|
||||
return dividend == Integer.MIN_VALUE ? 1 : 0;
|
||||
}
|
||||
// 考虑被除数为 0 的情况
|
||||
if (dividend == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
// 一般情况,使用类二分查找
|
||||
// 将所有的正数取相反数,这样就只需要考虑一种情况
|
||||
boolean rev = false;
|
||||
if (dividend > 0) {
|
||||
dividend = -dividend;
|
||||
rev = !rev;
|
||||
}
|
||||
if (divisor > 0) {
|
||||
divisor = -divisor;
|
||||
rev = !rev;
|
||||
}
|
||||
|
||||
List<Integer> candidates = new ArrayList<Integer>();
|
||||
candidates.add(divisor);
|
||||
int index = 0;
|
||||
// 注意溢出
|
||||
while (candidates.get(index) >= dividend - candidates.get(index)) {
|
||||
candidates.add(candidates.get(index) + candidates.get(index));
|
||||
++index;
|
||||
}
|
||||
int ans = 0;
|
||||
for (int i = candidates.size() - 1; i >= 0; --i) {
|
||||
if (candidates.get(i) >= dividend) {
|
||||
ans += 1 << i;
|
||||
dividend -= candidates.get(i);
|
||||
}
|
||||
}
|
||||
|
||||
return rev ? -ans : ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
public int Divide(int dividend, int divisor) {
|
||||
// 考虑被除数为最小值的情况
|
||||
if (dividend == int.MinValue) {
|
||||
if (divisor == 1) {
|
||||
return int.MinValue;
|
||||
}
|
||||
if (divisor == -1) {
|
||||
return int.MaxValue;
|
||||
}
|
||||
}
|
||||
// 考虑除数为最小值的情况
|
||||
if (divisor == int.MinValue) {
|
||||
return dividend == int.MinValue ? 1 : 0;
|
||||
}
|
||||
// 考虑被除数为 0 的情况
|
||||
if (dividend == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
// 一般情况,使用类二分查找
|
||||
// 将所有的正数取相反数,这样就只需要考虑一种情况
|
||||
bool rev = false;
|
||||
if (dividend > 0) {
|
||||
dividend = -dividend;
|
||||
rev = !rev;
|
||||
}
|
||||
if (divisor > 0) {
|
||||
divisor = -divisor;
|
||||
rev = !rev;
|
||||
}
|
||||
|
||||
IList<int> candidates = new List<int>();
|
||||
candidates.Add(divisor);
|
||||
int index = 0;
|
||||
// 注意溢出
|
||||
while (candidates[index] >= dividend - candidates[index]) {
|
||||
candidates.Add(candidates[index] + candidates[index]);
|
||||
++index;
|
||||
}
|
||||
int ans = 0;
|
||||
for (int i = candidates.Count - 1; i >= 0; --i) {
|
||||
if (candidates[i] >= dividend) {
|
||||
ans += 1 << i;
|
||||
dividend -= candidates[i];
|
||||
}
|
||||
}
|
||||
|
||||
return rev ? -ans : ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def divide(self, dividend: int, divisor: int) -> int:
|
||||
INT_MIN, INT_MAX = -2**31, 2**31 - 1
|
||||
|
||||
# 考虑被除数为最小值的情况
|
||||
if dividend == INT_MIN:
|
||||
if divisor == 1:
|
||||
return INT_MIN
|
||||
if divisor == -1:
|
||||
return INT_MAX
|
||||
|
||||
# 考虑除数为最小值的情况
|
||||
if divisor == INT_MIN:
|
||||
return 1 if dividend == INT_MIN else 0
|
||||
# 考虑被除数为 0 的情况
|
||||
if dividend == 0:
|
||||
return 0
|
||||
|
||||
# 一般情况,使用类二分查找
|
||||
# 将所有的正数取相反数,这样就只需要考虑一种情况
|
||||
rev = False
|
||||
if dividend > 0:
|
||||
dividend = -dividend
|
||||
rev = not rev
|
||||
if divisor > 0:
|
||||
divisor = -divisor
|
||||
rev = not rev
|
||||
|
||||
candidates = [divisor]
|
||||
# 注意溢出
|
||||
while candidates[-1] >= dividend - candidates[-1]:
|
||||
candidates.append(candidates[-1] + candidates[-1])
|
||||
|
||||
ans = 0
|
||||
for i in range(len(candidates) - 1, -1, -1):
|
||||
if candidates[i] >= dividend:
|
||||
ans += (1 << i)
|
||||
dividend -= candidates[i]
|
||||
|
||||
return -ans if rev else ans
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(\log C)$,即为二分查找需要的时间。方法二时间复杂度优于方法一的原因是:方法一的每一步二分查找都需要重新计算 $Z \times Y$ 的值,需要 $O(\log C)$ 的时间复杂度;而方法二的每一步的权重都是 $2$ 的幂,在二分查找开始前就都是已知的值,因此我们可以在 $O(\log C)$ 的时间内,一次性将它们全部预处理出来。
|
||||
|
||||
- 空间复杂度:$O(\log C)$,即为需要存储的 $Y \times 2^i$ 的数量。
|
||||
|
||||
@ -0,0 +1,142 @@
|
||||
#### 方法一:位运算
|
||||
|
||||
**思路与算法**
|
||||
|
||||
根据题目的要求,我们需要将 $\textit{num}$ 二进制表示的每一位取反。然而在计算机存储整数时,并不会仅仅存储有效的二进制位。例如当 $\textit{num} = 5$ 时,它的二进制表示为 $(101)_2$,而使用 $32$ 位整数存储时的结果为:
|
||||
|
||||
$$
|
||||
(0000~0000~0000~0000~0000~0000~0000~0101)_2
|
||||
$$
|
||||
|
||||
因此我们需要首先找到 $\textit{num}$ 二进制表示最高位的那个 $1$,再将这个 $1$ 以及更低的位进行取反。
|
||||
|
||||
如果 $\textit{num}$ 二进制表示最高位的 $1$ 是第 $i~(0 \leq i \leq 30)$ 位,那么一定有:
|
||||
|
||||
$$
|
||||
2^i \leq \textit < 2^{i+1}
|
||||
$$
|
||||
|
||||
因此我们可以使用一次遍历,在 $[0, 30]$ 中找出 $i$ 的值。
|
||||
|
||||
在这之后,我们就可以遍历 $\textit{num}$ 的第 $0 \sim i$ 个二进制位,将它们依次进行取反。我们也可以用更高效的方式,构造掩码 $\textit{mask} = 2^{i+1} - 1$,它是一个 $i+1$ 位的二进制数,并且每一位都是 $1$。我们将 $\textit{num}$ 与 $\textit{mask}$ 进行异或运算,即可得到答案。
|
||||
|
||||
**细节**
|
||||
|
||||
当 $i=30$ 时,构造 $\textit{mask} = 2^{i+1} - 1$ 的过程中需要保证不会产生整数溢出。下面部分语言的代码中对该情况进行了特殊判断。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int findComplement(int num) {
|
||||
int highbit = 0;
|
||||
for (int i = 1; i <= 30; ++i) {
|
||||
if (num >= (1 << i)) {
|
||||
highbit = i;
|
||||
}
|
||||
else {
|
||||
break;
|
||||
}
|
||||
}
|
||||
int mask = (highbit == 30 ? 0x7fffffff : (1 << (highbit + 1)) - 1);
|
||||
return num ^ mask;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int findComplement(int num) {
|
||||
int highbit = 0;
|
||||
for (int i = 1; i <= 30; ++i) {
|
||||
if (num >= 1 << i) {
|
||||
highbit = i;
|
||||
} else {
|
||||
break;
|
||||
}
|
||||
}
|
||||
int mask = highbit == 30 ? 0x7fffffff : (1 << (highbit + 1)) - 1;
|
||||
return num ^ mask;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
public int FindComplement(int num) {
|
||||
int highbit = 0;
|
||||
for (int i = 1; i <= 30; ++i) {
|
||||
if (num >= 1 << i) {
|
||||
highbit = i;
|
||||
} else {
|
||||
break;
|
||||
}
|
||||
}
|
||||
int mask = highbit == 30 ? 0x7fffffff : (1 << (highbit + 1)) - 1;
|
||||
return num ^ mask;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def findComplement(self, num: int) -> int:
|
||||
highbit = 0
|
||||
for i in range(1, 30 + 1):
|
||||
if num >= (1 << i):
|
||||
highbit = i
|
||||
else:
|
||||
break
|
||||
|
||||
mask = (1 << (highbit + 1)) - 1
|
||||
return num ^ mask
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var findComplement = function(num) {
|
||||
let highbit = 0;
|
||||
for (let i = 1; i <= 30; ++i) {
|
||||
if (num >= 1 << i) {
|
||||
highbit = i;
|
||||
} else {
|
||||
break;
|
||||
}
|
||||
}
|
||||
const mask = highbit == 30 ? 0x7fffffff : (1 << (highbit + 1)) - 1;
|
||||
return num ^ mask;
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func findComplement(num int) int {
|
||||
highBit := 0
|
||||
for i := 1; i <= 30; i++ {
|
||||
if num < 1<<i {
|
||||
break
|
||||
}
|
||||
highBit = i
|
||||
}
|
||||
mask := 1<<(highBit+1) - 1
|
||||
return num ^ mask
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(\log \textit{num})$。找出 $\textit{num}$ 二进制表示最高位的 $1$ 需要的时间为 $O(\log \textit{num})$。
|
||||
|
||||
- 空间复杂度:$O(1)$。
|
||||
|
||||
@ -0,0 +1,163 @@
|
||||
### 方法一:字典树
|
||||
|
||||
由于我们需要将 `searchWord` 的前缀与 `products` 中的字符串进行匹配,因此我们可以使用字典树(Trie)来存储 `products` 中的所有字符串。这样以来,当我们依次输入 `searchWord` 中的每个字母时,我们可以从字典树的根节点开始向下查找,判断是否存在以当前的输入为前缀的字符串,并找出字典序最小的三个(若存在)字符串。
|
||||
|
||||
对于字典树中的每个节点,我们需要额外地存储一些数据来帮助我们快速得到答案。设字典树中的某个节点为 `node`,从字典树的根到该节点对应的字符串为 `prefix`,那么我们可以在 `node` 中使用数组或优先队列,存放字典序最小的三个以 `prefix` 为前缀的字符串。具体的做法是:当我们在字典树中插入字符串 `product` 并遍历到节点 `node` 时,我们将 `product` 存储在 `node` 中,若此时 `node` 中的字符串超过三个,就丢弃字典序最大的那个字符串。这样在所有的字符串都被插入到字典树中后,字典树中的节点 `node` 就存放了当输入为 `prefix` 时应该返回的那些字符串。
|
||||
|
||||
* [sol1]
|
||||
|
||||
```C++
|
||||
struct Trie {
|
||||
unordered_map<char, Trie*> child;
|
||||
priority_queue<string> words;
|
||||
};
|
||||
|
||||
class Solution {
|
||||
private:
|
||||
void addWord(Trie* root, const string& word) {
|
||||
Trie* cur = root;
|
||||
for (const char& ch: word) {
|
||||
if (!cur->child.count(ch)) {
|
||||
cur->child[ch] = new Trie();
|
||||
}
|
||||
cur = cur->child[ch];
|
||||
cur->words.push(word);
|
||||
if (cur->words.size() > 3) {
|
||||
cur->words.pop();
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<string>> suggestedProducts(vector<string>& products, string searchWord) {
|
||||
Trie* root = new Trie();
|
||||
for (const string& word: products) {
|
||||
addWord(root, word);
|
||||
}
|
||||
|
||||
vector<vector<string>> ans;
|
||||
Trie* cur = root;
|
||||
bool flag = false;
|
||||
for (const char& ch: searchWord) {
|
||||
if (flag || !cur->child.count(ch)) {
|
||||
ans.emplace_back();
|
||||
flag = true;
|
||||
}
|
||||
else {
|
||||
cur = cur->child[ch];
|
||||
vector<string> selects;
|
||||
while (!cur->words.empty()) {
|
||||
selects.push_back(cur->words.top());
|
||||
cur->words.pop();
|
||||
}
|
||||
reverse(selects.begin(), selects.end());
|
||||
ans.push_back(move(selects));
|
||||
}
|
||||
}
|
||||
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1]
|
||||
|
||||
```Python
|
||||
class Trie:
|
||||
def __init__(self):
|
||||
self.child = dict()
|
||||
self.words = list()
|
||||
|
||||
class Solution:
|
||||
def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:
|
||||
def addWord(root, word):
|
||||
cur = root
|
||||
for ch in word:
|
||||
if ch not in cur.child:
|
||||
cur.child[ch] = Trie()
|
||||
cur = cur.child[ch]
|
||||
cur.words.append(word)
|
||||
cur.words.sort()
|
||||
if len(cur.words) > 3:
|
||||
cur.words.pop()
|
||||
|
||||
root = Trie()
|
||||
for word in products:
|
||||
addWord(root, word)
|
||||
|
||||
ans = list()
|
||||
cur = root
|
||||
flag = False
|
||||
for ch in searchWord:
|
||||
if flag or ch not in cur.child:
|
||||
ans.append(list())
|
||||
flag = True
|
||||
else:
|
||||
cur = cur.child[ch]
|
||||
ans.append(cur.words)
|
||||
|
||||
return ans
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(\sum L + S)$,其中 $\sum L$ 是所有字符串的长度之和,$S$ 是字符串 `searchWord` 的长度。在计算时间复杂度时,我们将字符串的平均长度视为常数,即在字典树中存储、比较和丢弃字符串的时间复杂度均为 $O(1)$。
|
||||
|
||||
- 空间复杂度:$O(\sum L)$。
|
||||
|
||||
### 方法二:二分查找
|
||||
|
||||
方法一中的字典树需要使用额外的空间。可以发现,字典树实际上是帮助我们完成了排序的工作。如果我们直接将数组 `products` 中的所有字符串按照字典序进行排序,那么对于输入单词 `searchWord` 的某个前缀 `prefix`,我们只需要在排完序的数组中找到最小的三个字典序大于等于 `prefix` 的字符串,并依次判断它们是否以 `prefix` 为前缀即可。由于在排完序的数组中,以 `prefix` 为前缀的字符串的位置一定是连续的,因此我们可以使用二分查找,找出最小的字典序大于等于 `prefix` 的字符串 `products[i]`,并依次判断 `products[i]`,`products[i + 1]` 和 `products[i + 2]` 是否以 `prefix` 为前缀即可。
|
||||
|
||||
此外,在我们输入单词 `seachWord` 中每个字母的过程中,`prefix` 的字典序是不断增大的。因此在每次二分查找时,我们可以将左边界设为上一次找到的位置 `i`,而不用从以 `0` 为左边界,这样可以减少每次二分查找中的查找次数(但不会减少时间复杂度的数量级)。
|
||||
|
||||
* [sol2]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
vector<vector<string>> suggestedProducts(vector<string>& products, string searchWord) {
|
||||
sort(products.begin(), products.end());
|
||||
string query;
|
||||
auto iter_last = products.begin();
|
||||
vector<vector<string>> ans;
|
||||
for (char ch: searchWord) {
|
||||
query += ch;
|
||||
auto iter_find = lower_bound(iter_last, products.end(), query);
|
||||
vector<string> selects;
|
||||
for (int i = 0; i < 3; ++i) {
|
||||
if (iter_find + i < products.end() && (*(iter_find + i)).find(query) == 0) {
|
||||
selects.push_back(*(iter_find + i));
|
||||
}
|
||||
}
|
||||
ans.push_back(move(selects));
|
||||
iter_last = iter_find;
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def suggestedProducts(self, products: List[str], searchWord: str) -> List[List[str]]:
|
||||
products.sort()
|
||||
query = ""
|
||||
iter_last = 0
|
||||
ans = list()
|
||||
for ch in searchWord:
|
||||
query += ch
|
||||
iter_find = bisect.bisect_left(products, query, iter_last)
|
||||
ans.append([s for s in products[iter_find : iter_find + 3] if s.startswith(query)])
|
||||
iter_last = iter_find
|
||||
return ans
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O\big((\sum L + S) * \log N\big)$,其中 $\sum L$ 是所有字符串的长度之和,$S$ 是字符串 `searchWord` 的长度,$N$ 是数组 `products` 的长度。对字符串进行排序的时间复杂度为 $O(\sum L * \log N)$,二分查找进行了 $L$ 次,每次查找的时间复杂度为 $\log N$。虽然方法二的时间复杂度高于方法一,但方法二的常数较小,因此实际运行速度要快于方法一。
|
||||
|
||||
- 空间复杂度:$O(\log N)$,为排序需要的空间复杂度。
|
||||
|
||||
@ -0,0 +1,161 @@
|
||||
### 📺 视频题解
|
||||
|
||||

|
||||
|
||||
### 📖 文字题解
|
||||
|
||||
#### 方法一:深度优先搜索
|
||||
|
||||
**思路和算法**
|
||||
|
||||
我们可以使用深度优先搜索的方式求出所有可能的路径。具体地,我们从 $0$ 号点出发,使用栈记录路径上的点。每次我们遍历到点 $n-1$,就将栈中记录的路径加入到答案中。
|
||||
|
||||
特别地,因为本题中的图为有向无环图($\text{DAG}$),搜索过程中不会反复遍历同一个点,因此我们无需判断当前点是否遍历过。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
vector<vector<int>> ans;
|
||||
vector<int> stk;
|
||||
|
||||
void dfs(vector<vector<int>>& graph, int x, int n) {
|
||||
if (x == n) {
|
||||
ans.push_back(stk);
|
||||
return;
|
||||
}
|
||||
for (auto& y : graph[x]) {
|
||||
stk.push_back(y);
|
||||
dfs(graph, y, n);
|
||||
stk.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
|
||||
stk.push_back(0);
|
||||
dfs(graph, 0, graph.size() - 1);
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
List<List<Integer>> ans = new ArrayList<List<Integer>>();
|
||||
Deque<Integer> stack = new ArrayDeque<Integer>();
|
||||
|
||||
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
|
||||
stack.offerLast(0);
|
||||
dfs(graph, 0, graph.length - 1);
|
||||
return ans;
|
||||
}
|
||||
|
||||
public void dfs(int[][] graph, int x, int n) {
|
||||
if (x == n) {
|
||||
ans.add(new ArrayList<Integer>(stack));
|
||||
return;
|
||||
}
|
||||
for (int y : graph[x]) {
|
||||
stack.offerLast(y);
|
||||
dfs(graph, y, n);
|
||||
stack.pollLast();
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
|
||||
ans = list()
|
||||
stk = list()
|
||||
|
||||
def dfs(x: int):
|
||||
if x == len(graph) - 1:
|
||||
ans.append(stk[:])
|
||||
return
|
||||
|
||||
for y in graph[x]:
|
||||
stk.append(y)
|
||||
dfs(y)
|
||||
stk.pop()
|
||||
|
||||
stk.append(0)
|
||||
dfs(0)
|
||||
return ans
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
int** ans;
|
||||
int stk[15];
|
||||
int stkSize;
|
||||
|
||||
void dfs(int x, int n, int** graph, int* graphColSize, int* returnSize, int** returnColumnSizes) {
|
||||
if (x == n) {
|
||||
int* tmp = malloc(sizeof(int) * stkSize);
|
||||
memcpy(tmp, stk, sizeof(int) * stkSize);
|
||||
ans[*returnSize] = tmp;
|
||||
(*returnColumnSizes)[(*returnSize)++] = stkSize;
|
||||
return;
|
||||
}
|
||||
for (int i = 0; i < graphColSize[x]; i++) {
|
||||
int y = graph[x][i];
|
||||
stk[stkSize++] = y;
|
||||
dfs(y, n, graph, graphColSize, returnSize, returnColumnSizes);
|
||||
stkSize--;
|
||||
}
|
||||
}
|
||||
|
||||
int** allPathsSourceTarget(int** graph, int graphSize, int* graphColSize, int* returnSize, int** returnColumnSizes) {
|
||||
stkSize = 0;
|
||||
stk[stkSize++] = 0;
|
||||
ans = malloc(sizeof(int*) * 16384);
|
||||
*returnSize = 0;
|
||||
*returnColumnSizes = malloc(sizeof(int) * 16384);
|
||||
dfs(0, graphSize - 1, graph, graphColSize, returnSize, returnColumnSizes);
|
||||
return ans;
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func allPathsSourceTarget(graph [][]int) (ans [][]int) {
|
||||
stk := []int{0}
|
||||
var dfs func(int)
|
||||
dfs = func(x int) {
|
||||
if x == len(graph)-1 {
|
||||
ans = append(ans, append([]int(nil), stk...))
|
||||
return
|
||||
}
|
||||
for _, y := range graph[x] {
|
||||
stk = append(stk, y)
|
||||
dfs(y)
|
||||
stk = stk[:len(stk)-1]
|
||||
}
|
||||
}
|
||||
dfs(0)
|
||||
return
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n \times 2^n)$,其中 $n$ 为图中点的数量。我们可以找到一种最坏情况,即每一个点都可以去往编号比它大的点。此时路径数为 $O(2^n)$,且每条路径长度为 $O(n)$,因此总时间复杂度为 $O(n \times 2^n)$。
|
||||
|
||||
- 空间复杂度:$O(n)$,其中 $n$ 为点的数量。主要为栈空间的开销。注意返回值不计入空间复杂度。
|
||||
|
||||
---
|
||||
|
||||
对于视频中提到的「有向无环图无需标记」更严谨的表述为「将有向图改成无向图」,如果需要了解该题目更加细致和扩展的内容,就现在,点击图片立刻前往 LeetBook,打牢基础,冲刺秋招!
|
||||
|
||||
[](https://leetcode-cn.com/leetbook/detail/graph/)
|
||||
@ -0,0 +1,141 @@
|
||||
### 思路
|
||||
|
||||
1. 先取出一行能够容纳的单词,将这些单词根据规则填入一行
|
||||
|
||||
2. 计算出**额外空格**的数量 `spaceCount`,**额外空格**就是正常书写用不到的空格
|
||||
21. 由总长度算起
|
||||
22. 除去每个单词末尾必须的空格,为了统一处理可以在结尾虚拟加上一个长度
|
||||
23. 除去所有单词的长度
|
||||
|
||||
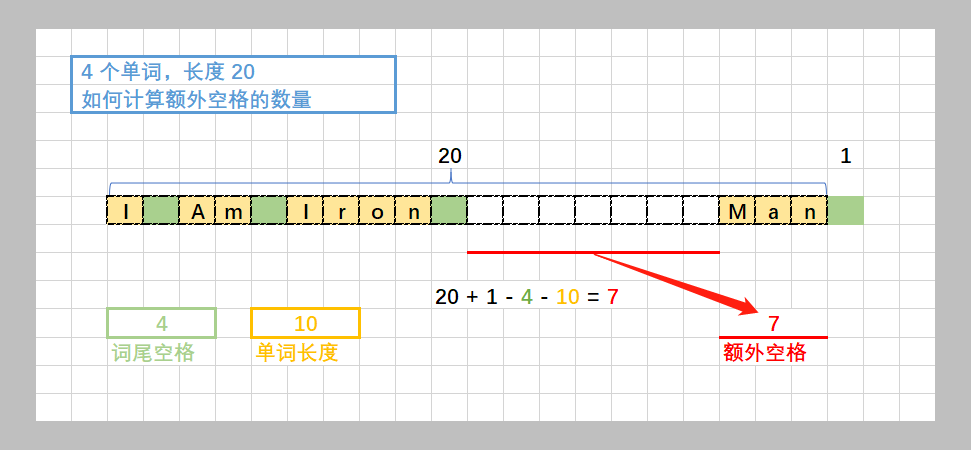
|
||||
|
||||
3. 按照单词的间隙数量 `wordCount - 1`,对**额外空格平均分布**
|
||||
|
||||
> **平均分布**可查看 【[另一篇题解](https://leetcode-cn.com/circle/discuss/eXOcnD/view/SecVmv/)】,简单来说就是商和余数的计算
|
||||
|
||||
31. 对于每个词填充之后,需要填充的空格数量等于 `spaceSuffix + spaceAvg + ((i - bg) < spaceExtra)`
|
||||
`spaceSuffix` 【单词尾部固定的空格】
|
||||
`spaceAvg` 【**额外空格**的平均值,每个间隙都要填入 spaceAvg 个空格】
|
||||
`((i - bg) < spaceExtra)` 【**额外空格**的余数,前 spaceExtra 个间隙需要多 1 个空格】
|
||||
|
||||
|
||||
|
||||
4. 特殊处理
|
||||
41. 一行只有一个单词,单词左对齐,右侧填满空格
|
||||
42. 最后一行,所有单词左对齐,中间只有一个空格,最后一个单词右侧填满空格
|
||||
|
||||
### 答题
|
||||
|
||||
* []
|
||||
|
||||
```C++
|
||||
string fillWords(vector<string>& words, int bg, int ed, int maxWidth, bool lastLine = false)
|
||||
{
|
||||
int wordCount = ed - bg + 1;
|
||||
int spaceCount = maxWidth + 1 - wordCount; // 除去每个单词尾部空格, + 1 是最后一个单词的尾部空格的特殊处理
|
||||
for (int i = bg; i <= ed; i++)
|
||||
{
|
||||
spaceCount -= words[i].size(); // 除去所有单词的长度
|
||||
}
|
||||
|
||||
int spaceSuffix = 1; // 词尾空格
|
||||
int spaceAvg = (wordCount == 1) ? 1 : spaceCount / (wordCount - 1); // 额外空格的平均值
|
||||
int spaceExtra = (wordCount == 1) ? 0 : spaceCount % (wordCount - 1); // 额外空格的余数
|
||||
|
||||
string ans;
|
||||
for (int i = bg; i < ed; i++)
|
||||
{
|
||||
ans += words[i]; // 填入单词
|
||||
if (lastLine) // 特殊处理最后一行
|
||||
{
|
||||
fill_n(back_inserter(ans), 1, ' ');
|
||||
continue;
|
||||
}
|
||||
fill_n(back_inserter(ans), spaceSuffix + spaceAvg + ((i - bg) < spaceExtra), ' '); // 根据计算结果补上空格
|
||||
}
|
||||
ans += words[ed]; // 填入最后一个单词
|
||||
fill_n(back_inserter(ans), maxWidth - ans.size(), ' '); // 补上这一行最后的空格
|
||||
return ans;
|
||||
}
|
||||
|
||||
vector<string> fullJustify(vector<string>& words, int maxWidth)
|
||||
{
|
||||
vector<string> ans;
|
||||
int cnt = 0;
|
||||
int bg = 0;
|
||||
for (int i = 0; i < words.size(); i++)
|
||||
{
|
||||
cnt += words[i].size() + 1;
|
||||
|
||||
if (i + 1 == words.size() || cnt + words[i + 1].size() > maxWidth)
|
||||
{ // 如果是最后一个单词,或者加上下一个词就超过长度了,即可凑成一行
|
||||
ans.push_back(fillWords(words, bg, i, maxWidth, i + 1 == words.size()));
|
||||
bg = i + 1;
|
||||
cnt = 0;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
```
|
||||
|
||||
* []
|
||||
|
||||
```C++
|
||||
string fillWords(vector<string>& words, int bg, int ed, int maxWidth, bool lastLine = false)
|
||||
{
|
||||
int wordCount = ed - bg + 1;
|
||||
int spaceCount = maxWidth + 1 - wordCount;
|
||||
for (int i = bg; i <= ed; i++)
|
||||
{
|
||||
spaceCount -= words[i].size();
|
||||
}
|
||||
|
||||
int spaceSuffix = 1;
|
||||
int spaceAvg = (wordCount == 1) ? 1 : spaceCount / (wordCount - 1);
|
||||
int spaceExtra = (wordCount == 1) ? 0 : spaceCount % (wordCount - 1);
|
||||
|
||||
string ans;
|
||||
for (int i = bg; i < ed; i++)
|
||||
{
|
||||
ans += words[i];
|
||||
if (lastLine)
|
||||
{
|
||||
fill_n(back_inserter(ans), 1, ' ');
|
||||
continue;
|
||||
}
|
||||
fill_n(back_inserter(ans), spaceSuffix + spaceAvg + ((i - bg) < spaceExtra), ' ');
|
||||
}
|
||||
ans += words[ed];
|
||||
fill_n(back_inserter(ans), maxWidth - ans.size(), ' ');
|
||||
return ans;
|
||||
}
|
||||
|
||||
vector<string> fullJustify(vector<string>& words, int maxWidth)
|
||||
{
|
||||
vector<string> ans;
|
||||
int cnt = 0;
|
||||
int bg = 0;
|
||||
for (int i = 0; i < words.size(); i++)
|
||||
{
|
||||
cnt += words[i].size() + 1;
|
||||
|
||||
if (i + 1 == words.size() || cnt + words[i + 1].size() > maxWidth)
|
||||
{
|
||||
ans.push_back(fillWords(words, bg, i, maxWidth, i + 1 == words.size()));
|
||||
bg = i + 1;
|
||||
cnt = 0;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
```
|
||||
|
||||
### 执行时间
|
||||
|
||||

|
||||
|
||||
### 致谢
|
||||
|
||||
感谢您的观看,希望对您有帮助,欢迎热烈的交流!
|
||||
|
||||
**如果感觉还不错就点个赞吧~**
|
||||
@ -0,0 +1,153 @@
|
||||
#### 方法一:双指针
|
||||
|
||||
我们可以枚举字符串中的每一个位置作为右端点,然后找到其最远的左端点的位置,满足该区间内除了出现次数最多的那一类字符之外,剩余的字符(即非最长重复字符)数量不超过 $k$ 个。
|
||||
|
||||
这样我们可以想到使用双指针维护这些区间,每次右指针右移,如果区间仍然满足条件,那么左指针不移动,否则左指针至多右移一格,保证区间长度不减小。
|
||||
|
||||
虽然这样的操作会导致部分区间不符合条件,即该区间内非最长重复字符超过了 $k$ 个。但是这样的区间也同样不可能对答案产生贡献。当我们右指针移动到尽头,左右指针对应的区间的长度必然对应一个长度最大的符合条件的区间。
|
||||
|
||||
实际代码中,由于字符串中仅包含大写字母,我们可以使用一个长度为 $26$ 的数组维护每一个字符的出现次数。每次区间右移,我们更新右移位置的字符出现的次数,然后尝试用它更新重复字符出现次数的历史最大值,最后我们使用该最大值计算出区间内非最长重复字符的数量,以此判断左指针是否需要右移即可。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int characterReplacement(string s, int k) {
|
||||
vector<int> num(26);
|
||||
int n = s.length();
|
||||
int maxn = 0;
|
||||
int left = 0, right = 0;
|
||||
while (right < n) {
|
||||
num[s[right] - 'A']++;
|
||||
maxn = max(maxn, num[s[right] - 'A']);
|
||||
if (right - left + 1 - maxn > k) {
|
||||
num[s[left] - 'A']--;
|
||||
left++;
|
||||
}
|
||||
right++;
|
||||
}
|
||||
return right - left;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int characterReplacement(String s, int k) {
|
||||
int[] num = new int[26];
|
||||
int n = s.length();
|
||||
int maxn = 0;
|
||||
int left = 0, right = 0;
|
||||
while (right < n) {
|
||||
num[s.charAt(right) - 'A']++;
|
||||
maxn = Math.max(maxn, num[s.charAt(right) - 'A']);
|
||||
if (right - left + 1 - maxn > k) {
|
||||
num[s.charAt(left) - 'A']--;
|
||||
left++;
|
||||
}
|
||||
right++;
|
||||
}
|
||||
return right - left;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func characterReplacement(s string, k int) int {
|
||||
cnt := [26]int{}
|
||||
maxCnt, left := 0, 0
|
||||
for right, ch := range s {
|
||||
cnt[ch-'A']++
|
||||
maxCnt = max(maxCnt, cnt[ch-'A'])
|
||||
if right-left+1-maxCnt > k {
|
||||
cnt[s[left]-'A']--
|
||||
left++
|
||||
}
|
||||
}
|
||||
return len(s) - left
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
int characterReplacement(char* s, int k) {
|
||||
int num[26];
|
||||
memset(num, 0, sizeof(num));
|
||||
int n = strlen(s);
|
||||
int maxn = 0;
|
||||
int left = 0, right = 0;
|
||||
while (right < n) {
|
||||
num[s[right] - 'A']++;
|
||||
maxn = fmax(maxn, num[s[right] - 'A']);
|
||||
if (right - left + 1 - maxn > k) {
|
||||
num[s[left] - 'A']--;
|
||||
left++;
|
||||
}
|
||||
right++;
|
||||
}
|
||||
return right - left;
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def characterReplacement(self, s: str, k: int) -> int:
|
||||
num = [0] * 26
|
||||
n = len(s)
|
||||
maxn = left = right = 0
|
||||
|
||||
while right < n:
|
||||
num[ord(s[right]) - ord("A")] += 1
|
||||
maxn = max(maxn, num[ord(s[right]) - ord("A")])
|
||||
if right - left + 1 - maxn > k:
|
||||
num[ord(s[left]) - ord("A")] -= 1
|
||||
left += 1
|
||||
right += 1
|
||||
|
||||
return right - left
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var characterReplacement = function(s, k) {
|
||||
const num = new Array(26).fill(0);
|
||||
const n = s.length;
|
||||
let maxn = 0, left = 0, right = 0;
|
||||
|
||||
while (right < n) {
|
||||
num[s[right].charCodeAt() - 'A'.charCodeAt()]++;
|
||||
maxn = Math.max(maxn, num[s[right].charCodeAt() - 'A'.charCodeAt()])
|
||||
if (right - left + 1 - maxn > k) {
|
||||
num[s[left].charCodeAt() - 'A'.charCodeAt()]--;
|
||||
left++;
|
||||
}
|
||||
right++;
|
||||
}
|
||||
return right - left;
|
||||
};
|
||||
```
|
||||
|
||||
**时间复杂度**
|
||||
|
||||
- 时间复杂度:$O(n)$,其中 $n$ 是字符串的长度。我们至多只需要遍历该字符串一次。
|
||||
|
||||
- 空间复杂度:$O(|\Sigma|)$,其中 $|\Sigma|$ 是字符集的大小。我们需要存储每个大写英文字母的出现次数。
|
||||
|
||||
@ -0,0 +1,404 @@
|
||||
#### 方法一:字典树
|
||||
|
||||
**预备知识**
|
||||
|
||||
字典树(前缀树)是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。前缀树可以用 $O(|S|)$ 的时间复杂度完成如下操作,其中 $|S|$ 是插入字符串或查询前缀的长度:
|
||||
|
||||
- 向字典树中插入字符串 $\textit{word}$;
|
||||
|
||||
- 查询字符串 $\textit{word}$ 是否已经插入到字典树中。
|
||||
|
||||
字典树的实现可以参考「[208. 实现 Trie (前缀树) 的官方题解](https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/shi-xian-trie-qian-zhui-shu-by-leetcode-ti500/)」。
|
||||
|
||||
**思路和算法**
|
||||
|
||||
根据题意,$\texttt{WordDictionary}$ 类需要支持添加单词和搜索单词的操作,可以使用字典树实现。
|
||||
|
||||
对于添加单词,将单词添加到字典树中即可。
|
||||
|
||||
对于搜索单词,从字典树的根结点开始搜索。由于待搜索的单词可能包含点号,因此在搜索过程中需要考虑点号的处理。对于当前字符是字母和点号的情况,分别按照如下方式处理:
|
||||
|
||||
- 如果当前字符是字母,则判断当前字符对应的子结点是否存在,如果子结点存在则移动到子结点,继续搜索下一个字符,如果子结点不存在则说明单词不存在,返回 $\text{false}$;
|
||||
|
||||
- 如果当前字符是点号,由于点号可以表示任何字母,因此需要对当前结点的所有非空子结点继续搜索下一个字符。
|
||||
|
||||
重复上述步骤,直到返回 $\text{false}$ 或搜索完给定单词的最后一个字符。
|
||||
|
||||
如果搜索完给定的单词的最后一个字符,则当搜索到的最后一个结点的 $\textit{isEnd}$ 为 $\text{true}$ 时,给定的单词存在。
|
||||
|
||||
特别地,当搜索到点号时,只要存在一个非空子结点可以搜索到给定的单词,即返回 $\text{true}$。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class WordDictionary {
|
||||
private Trie root;
|
||||
|
||||
public WordDictionary() {
|
||||
root = new Trie();
|
||||
}
|
||||
|
||||
public void addWord(String word) {
|
||||
root.insert(word);
|
||||
}
|
||||
|
||||
public boolean search(String word) {
|
||||
return dfs(word, 0, root);
|
||||
}
|
||||
|
||||
private boolean dfs(String word, int index, Trie node) {
|
||||
if (index == word.length()) {
|
||||
return node.isEnd();
|
||||
}
|
||||
char ch = word.charAt(index);
|
||||
if (Character.isLetter(ch)) {
|
||||
int childIndex = ch - 'a';
|
||||
Trie child = node.getChildren()[childIndex];
|
||||
if (child != null && dfs(word, index + 1, child)) {
|
||||
return true;
|
||||
}
|
||||
} else {
|
||||
for (int i = 0; i < 26; i++) {
|
||||
Trie child = node.getChildren()[i];
|
||||
if (child != null && dfs(word, index + 1, child)) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
}
|
||||
|
||||
class Trie {
|
||||
private Trie[] children;
|
||||
private boolean isEnd;
|
||||
|
||||
public Trie() {
|
||||
children = new Trie[26];
|
||||
isEnd = false;
|
||||
}
|
||||
|
||||
public void insert(String word) {
|
||||
Trie node = this;
|
||||
for (int i = 0; i < word.length(); i++) {
|
||||
char ch = word.charAt(i);
|
||||
int index = ch - 'a';
|
||||
if (node.children[index] == null) {
|
||||
node.children[index] = new Trie();
|
||||
}
|
||||
node = node.children[index];
|
||||
}
|
||||
node.isEnd = true;
|
||||
}
|
||||
|
||||
public Trie[] getChildren() {
|
||||
return children;
|
||||
}
|
||||
|
||||
public boolean isEnd() {
|
||||
return isEnd;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class WordDictionary {
|
||||
private Trie root;
|
||||
|
||||
public WordDictionary() {
|
||||
root = new Trie();
|
||||
}
|
||||
|
||||
public void AddWord(string word) {
|
||||
root.Insert(word);
|
||||
}
|
||||
|
||||
public bool Search(string word) {
|
||||
return DFS(word, 0, root);
|
||||
}
|
||||
|
||||
private bool DFS(String word, int index, Trie node) {
|
||||
if (index == word.Length) {
|
||||
return node.IsEnd;
|
||||
}
|
||||
char ch = word[index];
|
||||
if (char.IsLetter(ch)) {
|
||||
int childIndex = ch - 'a';
|
||||
Trie child = node.Children[childIndex];
|
||||
if (child != null && DFS(word, index + 1, child)) {
|
||||
return true;
|
||||
}
|
||||
} else {
|
||||
for (int i = 0; i < 26; i++) {
|
||||
Trie child = node.Children[i];
|
||||
if (child != null && DFS(word, index + 1, child)) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
}
|
||||
|
||||
class Trie {
|
||||
public Trie[] Children { get; }
|
||||
public bool IsEnd { get; set; }
|
||||
|
||||
public Trie() {
|
||||
Children = new Trie[26];
|
||||
IsEnd = false;
|
||||
}
|
||||
|
||||
public void Insert(String word) {
|
||||
Trie node = this;
|
||||
for (int i = 0; i < word.Length; i++) {
|
||||
char ch = word[i];
|
||||
int index = ch - 'a';
|
||||
if (node.Children[index] == null) {
|
||||
node.Children[index] = new Trie();
|
||||
}
|
||||
node = node.Children[index];
|
||||
}
|
||||
node.IsEnd = true;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
struct TrieNode{
|
||||
vector<TrieNode *> child;
|
||||
bool isEnd;
|
||||
TrieNode() {
|
||||
this->child = vector<TrieNode *>(26,nullptr);
|
||||
this->isEnd = false;
|
||||
}
|
||||
};
|
||||
|
||||
void insert(TrieNode * root, const string & word) {
|
||||
TrieNode * node = root;
|
||||
for (auto c : word) {
|
||||
if (node->child[c - 'a'] == nullptr) {
|
||||
node->child[c - 'a'] = new TrieNode();
|
||||
}
|
||||
node = node->child[c - 'a'];
|
||||
}
|
||||
node->isEnd = true;
|
||||
}
|
||||
|
||||
class WordDictionary {
|
||||
public:
|
||||
WordDictionary() {
|
||||
trie = new TrieNode();
|
||||
}
|
||||
|
||||
void addWord(string word) {
|
||||
insert(trie,word);
|
||||
}
|
||||
|
||||
bool search(string word) {
|
||||
return dfs(word, 0, trie);
|
||||
}
|
||||
|
||||
bool dfs(const string & word,int index,TrieNode * node) {
|
||||
if (index == word.size()) {
|
||||
return node->isEnd;
|
||||
}
|
||||
char ch = word[index];
|
||||
if (ch >= 'a' && ch <= 'z') {
|
||||
TrieNode * child = node->child[ch - 'a'];
|
||||
if (child != nullptr && dfs(word, index + 1, child)) {
|
||||
return true;
|
||||
}
|
||||
} else if (ch == '.') {
|
||||
for (int i = 0; i < 26; i++) {
|
||||
TrieNode * child = node->child[i];
|
||||
if (child != nullptr && dfs(word, index + 1, child)) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
private:
|
||||
TrieNode * trie;
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
type TrieNode struct {
|
||||
children [26]*TrieNode
|
||||
isEnd bool
|
||||
}
|
||||
|
||||
func (t *TrieNode) Insert(word string) {
|
||||
node := t
|
||||
for _, ch := range word {
|
||||
ch -= 'a'
|
||||
if node.children[ch] == nil {
|
||||
node.children[ch] = &TrieNode{}
|
||||
}
|
||||
node = node.children[ch]
|
||||
}
|
||||
node.isEnd = true
|
||||
}
|
||||
|
||||
type WordDictionary struct {
|
||||
trieRoot *TrieNode
|
||||
}
|
||||
|
||||
func Constructor() WordDictionary {
|
||||
return WordDictionary{&TrieNode{}}
|
||||
}
|
||||
|
||||
func (d *WordDictionary) AddWord(word string) {
|
||||
d.trieRoot.Insert(word)
|
||||
}
|
||||
|
||||
func (d *WordDictionary) Search(word string) bool {
|
||||
var dfs func(int, *TrieNode) bool
|
||||
dfs = func(index int, node *TrieNode) bool {
|
||||
if index == len(word) {
|
||||
return node.isEnd
|
||||
}
|
||||
ch := word[index]
|
||||
if ch != '.' {
|
||||
child := node.children[ch-'a']
|
||||
if child != nil && dfs(index+1, child) {
|
||||
return true
|
||||
}
|
||||
} else {
|
||||
for i := range node.children {
|
||||
child := node.children[i]
|
||||
if child != nil && dfs(index+1, child) {
|
||||
return true
|
||||
}
|
||||
}
|
||||
}
|
||||
return false
|
||||
}
|
||||
return dfs(0, d.trieRoot)
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class TrieNode:
|
||||
def __init__(self):
|
||||
self.children = [None] * 26
|
||||
self.isEnd = False
|
||||
|
||||
def insert(self, word: str) -> None:
|
||||
node = self
|
||||
for ch in word:
|
||||
ch = ord(ch) - ord('a')
|
||||
if not node.children[ch]:
|
||||
node.children[ch] = TrieNode()
|
||||
node = node.children[ch]
|
||||
node.isEnd = True
|
||||
|
||||
|
||||
class WordDictionary:
|
||||
def __init__(self):
|
||||
self.trieRoot = TrieNode()
|
||||
|
||||
def addWord(self, word: str) -> None:
|
||||
self.trieRoot.insert(word)
|
||||
|
||||
def search(self, word: str) -> bool:
|
||||
def dfs(index: int, node: TrieNode) -> bool:
|
||||
if index == len(word):
|
||||
return node.isEnd
|
||||
ch = word[index]
|
||||
if ch != '.':
|
||||
child = node.children[ord(ch) - ord('a')]
|
||||
if child is not None and dfs(index + 1, child):
|
||||
return True
|
||||
else:
|
||||
for child in node.children:
|
||||
if child is not None and dfs(index + 1, child):
|
||||
return True
|
||||
return False
|
||||
|
||||
return dfs(0, self.trieRoot)
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var WordDictionary = function() {
|
||||
this.trieRoot = new TrieNode();
|
||||
};
|
||||
|
||||
WordDictionary.prototype.addWord = function(word) {
|
||||
this.trieRoot.insert(word);
|
||||
};
|
||||
|
||||
WordDictionary.prototype.search = function(word) {
|
||||
const dfs = (index, node) => {
|
||||
if (index === word.length) {
|
||||
return node.isEnd;
|
||||
}
|
||||
const ch = word[index];
|
||||
if (ch !== '.') {
|
||||
const child = node.children[ch.charCodeAt() - 'a'.charCodeAt()]
|
||||
if (child && dfs(index + 1, child)) {
|
||||
return true;
|
||||
}
|
||||
} else {
|
||||
for (const child of node.children) {
|
||||
if (child && dfs(index + 1, child)) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
|
||||
return dfs(0, this.trieRoot);
|
||||
};
|
||||
|
||||
class TrieNode {
|
||||
constructor() {
|
||||
this.children = new Array(26).fill(0);
|
||||
this.isEnd = false;
|
||||
}
|
||||
|
||||
insert(word) {
|
||||
let node = this;
|
||||
for (let i = 0; i < word.length; i++) {
|
||||
const ch = word[i];
|
||||
const index = ch.charCodeAt() - 'a'.charCodeAt();
|
||||
if (node.children[index] === 0) {
|
||||
node.children[index] = new TrieNode();
|
||||
}
|
||||
node = node.children[index];
|
||||
}
|
||||
node.isEnd = true;
|
||||
}
|
||||
|
||||
getChildren() {
|
||||
return this.children;
|
||||
}
|
||||
|
||||
isEnd() {
|
||||
return this.isEnd;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:初始化为 $O(1)$,添加单词为 $O(|S|)$,搜索单词为 $O(|\Sigma|^{|S|})$,其中 $|S|$ 是每次添加或搜索的单词的长度,$\Sigma$ 是字符集,这道题中的字符集为全部小写英语字母,$|\Sigma| = 26$。
|
||||
最坏情况下,待搜索的单词中的每个字符都是点号,则每个字符都有 $|\Sigma|$ 种可能。
|
||||
|
||||
- 空间复杂度:$O(|T|\cdot|\Sigma|)$,其中 $|T|$ 是所有添加的单词的长度之和,$\Sigma$ 是字符集,这道题中的字符集为全部小写英语字母,$|\Sigma| = 26$。
|
||||
|
||||
@ -0,0 +1,470 @@
|
||||
#### 方法一:双指针
|
||||
|
||||
**思路和算法**
|
||||
|
||||
根据题意,我们需要解决两个问题:
|
||||
|
||||
- 如何判断 $\textit{dictionary}$ 中的字符串 $t$ 是否可以通过删除 $s$ 中的某些字符得到;
|
||||
|
||||
- 如何找到长度最长且字典序最小的字符串。
|
||||
|
||||
第 $1$ 个问题实际上就是判断 $t$ 是否是 $s$ 的子序列。因此只要能找到任意一种 $t$ 在 $s$ 中出现的方式,即可认为 $t$ 是 $s$ 的子序列。而当我们从前往后匹配时,可以发现每次贪心地匹配最靠前的字符是最优决策。
|
||||
|
||||
> 假定当前需要匹配字符 $c$,而字符 $c$ 在 $s$ 中的位置 $x_1$ 和 $x_2$ 出现($x_1 < x_2$),那么贪心取 $x_1$ 是最优解,因为 $x_2$ 后面能取到的字符,$x_1$ 也都能取到,并且通过 $x_1$ 与 $x_2$ 之间的可选字符,更有希望能匹配成功。
|
||||
|
||||
这样,我们初始化两个指针 $i$ 和 $j$,分别指向 $t$ 和 $s$ 的初始位置。每次贪心地匹配,匹配成功则 $i$ 和 $j$ 同时右移,匹配 $t$ 的下一个位置,匹配失败则 $j$ 右移,$i$ 不变,尝试用 $s$ 的下一个字符匹配 $t$。
|
||||
|
||||
最终如果 $i$ 移动到 $t$ 的末尾,则说明 $t$ 是 $s$ 的子序列。
|
||||
|
||||
第 $2$ 个问题可以通过遍历 $\textit{dictionary}$ 中的字符串,并维护当前长度最长且字典序最小的字符串来找到。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def findLongestWord(self, s: str, dictionary: List[str]) -> str:
|
||||
res = ""
|
||||
for t in dictionary:
|
||||
i = j = 0
|
||||
while i < len(t) and j < len(s):
|
||||
if t[i] == s[j]:
|
||||
i += 1
|
||||
j += 1
|
||||
if i == len(t):
|
||||
if len(t) > len(res) or (len(t) == len(res) and t < res):
|
||||
res = t
|
||||
return res
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public String findLongestWord(String s, List<String> dictionary) {
|
||||
String res = "";
|
||||
for (String t : dictionary) {
|
||||
int i = 0, j = 0;
|
||||
while (i < t.length() && j < s.length()) {
|
||||
if (t.charAt(i) == s.charAt(j)) {
|
||||
++i;
|
||||
}
|
||||
++j;
|
||||
}
|
||||
if (i == t.length()) {
|
||||
if (t.length() > res.length() || (t.length() == res.length() && t.compareTo(res) < 0)) {
|
||||
res = t;
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
public string FindLongestWord(string s, IList<string> dictionary) {
|
||||
string res = "";
|
||||
foreach (string t in dictionary) {
|
||||
int i = 0, j = 0;
|
||||
while (i < t.Length && j < s.Length) {
|
||||
if (t[i] == s[j]) {
|
||||
++i;
|
||||
}
|
||||
++j;
|
||||
}
|
||||
if (i == t.Length) {
|
||||
if (t.Length > res.Length || (t.Length == res.Length && t.CompareTo(res) < 0)) {
|
||||
res = t;
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func findLongestWord(s string, dictionary []string) (ans string) {
|
||||
for _, t := range dictionary {
|
||||
i := 0
|
||||
for j := range s {
|
||||
if s[j] == t[i] {
|
||||
i++
|
||||
if i == len(t) {
|
||||
if len(t) > len(ans) || len(t) == len(ans) && t < ans {
|
||||
ans = t
|
||||
}
|
||||
break
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
return
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var findLongestWord = function(s, dictionary) {
|
||||
let res = "";
|
||||
for (const t of dictionary) {
|
||||
let i = 0, j = 0;
|
||||
while (i < t.length && j < s.length) {
|
||||
if (t[i] === s[j]) {
|
||||
++i;
|
||||
}
|
||||
++j;
|
||||
}
|
||||
if (i === t.length) {
|
||||
if (t.length > res.length || (t.length === res.length && t < res)) {
|
||||
res = t;
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(d \times (m+n))$,其中 $d$ 表示 $\textit{dictionary}$ 的长度,$m$ 表示 $s$ 的长度,$n$ 表示 $\textit{dictionary}$ 中字符串的平均长度。我们需要遍历 $\textit{dictionary}$ 中的 $d$ 个字符串,每个字符串需要 $O(n+m)$ 的时间复杂度来判断该字符串是否为 $s$ 的子序列。
|
||||
|
||||
- 空间复杂度:$O(1)$。
|
||||
|
||||
#### 方法二:排序
|
||||
|
||||
**思路和算法**
|
||||
|
||||
在方法一的基础上,我们尝试通过对 $\textit{dictionary}$ 的预处理,来优化第 $2$ 个问题的处理。
|
||||
|
||||
我们可以先将 $\textit{dictionary}$ 依据字符串长度的降序和字典序的升序进行排序,然后从前向后找到第一个符合条件的字符串直接返回即可。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol2-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def findLongestWord(self, s: str, dictionary: List[str]) -> str:
|
||||
dictionary.sort(key=lambda x: (-len(x), x))
|
||||
for t in dictionary:
|
||||
i = j = 0
|
||||
while i < len(t) and j < len(s):
|
||||
if t[i] == s[j]:
|
||||
i += 1
|
||||
j += 1
|
||||
if i == len(t):
|
||||
return t
|
||||
return ""
|
||||
```
|
||||
|
||||
* [sol2-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public String findLongestWord(String s, List<String> dictionary) {
|
||||
Collections.sort(dictionary, new Comparator<String>() {
|
||||
public int compare(String word1, String word2) {
|
||||
if (word1.length() != word2.length()) {
|
||||
return word2.length() - word1.length();
|
||||
} else {
|
||||
return word1.compareTo(word2);
|
||||
}
|
||||
}
|
||||
});
|
||||
for (String t : dictionary) {
|
||||
int i = 0, j = 0;
|
||||
while (i < t.length() && j < s.length()) {
|
||||
if (t.charAt(i) == s.charAt(j)) {
|
||||
++i;
|
||||
}
|
||||
++j;
|
||||
}
|
||||
if (i == t.length()) {
|
||||
return t;
|
||||
}
|
||||
}
|
||||
return "";
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Golang]
|
||||
|
||||
```go
|
||||
func findLongestWord(s string, dictionary []string) string {
|
||||
sort.Slice(dictionary, func(i, j int) bool {
|
||||
a, b := dictionary[i], dictionary[j]
|
||||
return len(a) > len(b) || len(a) == len(b) && a < b
|
||||
})
|
||||
for _, t := range dictionary {
|
||||
i := 0
|
||||
for j := range s {
|
||||
if s[j] == t[i] {
|
||||
i++
|
||||
if i == len(t) {
|
||||
return t
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
return ""
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var findLongestWord = function(s, dictionary) {
|
||||
dictionary.sort((word1, word2) => {
|
||||
if (word1.length !== word2.length) {
|
||||
return word2.length - word1.length;
|
||||
} else {
|
||||
return word1.localeCompare(word2);
|
||||
}
|
||||
});
|
||||
console.log(dictionary)
|
||||
|
||||
for (const t of dictionary) {
|
||||
let i = 0, j = 0;
|
||||
while (i < t.length && j < s.length) {
|
||||
if (t[i] === s[j]) {
|
||||
++i;
|
||||
}
|
||||
++j;
|
||||
}
|
||||
if (i === t.length) {
|
||||
return t;
|
||||
}
|
||||
}
|
||||
return "";
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(d \times m \times \log d + d \times (m+n))$,其中 $d$ 表示 $\textit{dictionary}$ 的长度,$m$ 表示 $s$ 的长度,$n$ 表示 $\textit{dictionary}$ 中字符串的平均长度。我们需要 $O(d \times m \times \log d)$ 的时间来排序 $\textit{dictionary}$;在最坏的情况下,我们需要 $O(d \times (m+n))$ 来找到第一个符合条件的字符串。
|
||||
|
||||
- 空间复杂度:$O(d \times m)$,为排序的开销。
|
||||
|
||||
#### 方法三:动态规划
|
||||
|
||||
**思路和算法**
|
||||
|
||||
在方法一的基础上,我们考虑通过对字符串 $s$ 的预处理,来优化第 $1$ 个问题的处理。
|
||||
|
||||
考虑前面的双指针的做法,我们注意到我们有大量的时间用于在 $s$ 中找到下一个匹配字符。
|
||||
|
||||
这样我们通过预处理,得到:对于 $s$ 的每一个位置,从该位置开始往后每一个字符第一次出现的位置。
|
||||
|
||||
我们可以使用动态规划的方法实现预处理,令 $f[i][j]$ 表示字符串 $s$ 中从位置 $i$ 开始往后字符 $j$ 第一次出现的位置。在进行状态转移时,如果 $s$ 中位置 $i$ 的字符就是 $j$,那么 $f[i][j]=i$,否则 $j$ 出现在位置 $i+1$ 开始往后,即 $f[i][j]=f[i+1][j]$;因此我们要倒过来进行动态规划,从后往前枚举 $i$。
|
||||
|
||||
这样我们可以写出状态转移方程:
|
||||
$$
|
||||
f[i][j]=
|
||||
\begin
|
||||
i, & s[i]=j \\
|
||||
f[i+1][j], & s[i] \ne j
|
||||
\end
|
||||
$$
|
||||
假定下标从 $0$ 开始,那么 $f[i][j]$ 中有 $0 \leq i \leq m-1$ ,对于边界状态 $f[m-1][..]$,我们置 $f[m][..]$ 为 $m$,让 $f[m-1][..]$ 正常进行转移。这样如果 $f[i][j]=m$,则表示从位置 $i$ 开始往后不存在字符 $j$。
|
||||
|
||||
这样,我们可以利用 $f$ 数组,每次 $O(1)$ 地跳转到下一个位置,直到位置变为 $m$ 或 $t$ 中的每一个字符都匹配成功。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol3-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def findLongestWord(self, s: str, dictionary: List[str]) -> str:
|
||||
m = len(s)
|
||||
f = [[0] * 26 for _ in range(m)]
|
||||
f.append([m] * 26)
|
||||
|
||||
for i in range(m - 1, -1, -1):
|
||||
for j in range(26):
|
||||
if ord(s[i]) == j + 97:
|
||||
f[i][j] = i
|
||||
else:
|
||||
f[i][j] = f[i + 1][j]
|
||||
|
||||
res = ""
|
||||
for t in dictionary:
|
||||
match = True
|
||||
j = 0
|
||||
for i in range(len(t)):
|
||||
if f[j][ord(t[i]) - 97] == m:
|
||||
match = False
|
||||
break
|
||||
j = f[j][ord(t[i]) - 97] + 1
|
||||
if match:
|
||||
if len(t) > len(res) or (len(t) == len(res) and t < res):
|
||||
res = t
|
||||
return res
|
||||
```
|
||||
|
||||
* [sol3-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public String findLongestWord(String s, List<String> dictionary) {
|
||||
int m = s.length();
|
||||
int[][] f = new int[m + 1][26];
|
||||
Arrays.fill(f[m], m);
|
||||
|
||||
for (int i = m - 1; i >= 0; --i) {
|
||||
for (int j = 0; j < 26; ++j) {
|
||||
if (s.charAt(i) == (char) ('a' + j)) {
|
||||
f[i][j] = i;
|
||||
} else {
|
||||
f[i][j] = f[i + 1][j];
|
||||
}
|
||||
}
|
||||
}
|
||||
String res = "";
|
||||
for (String t : dictionary) {
|
||||
boolean match = true;
|
||||
int j = 0;
|
||||
for (int i = 0; i < t.length(); ++i) {
|
||||
if (f[j][t.charAt(i) - 'a'] == m) {
|
||||
match = false;
|
||||
break;
|
||||
}
|
||||
j = f[j][t.charAt(i) - 'a'] + 1;
|
||||
}
|
||||
if (match) {
|
||||
if (t.length() > res.length() || (t.length() == res.length() && t.compareTo(res) < 0)) {
|
||||
res = t;
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol3-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
public string FindLongestWord(string s, IList<string> dictionary) {
|
||||
int m = s.Length;
|
||||
int[,] f = new int[m + 1, 26];
|
||||
for (int j = 0; j < 26; ++j) {
|
||||
f[m, j] = m;
|
||||
}
|
||||
|
||||
for (int i = m - 1; i >= 0; --i) {
|
||||
for (int j = 0; j < 26; j++) {
|
||||
if (s[i] == (char) ('a' + j)) {
|
||||
f[i, j] = i;
|
||||
} else {
|
||||
f[i, j] = f[i + 1, j];
|
||||
}
|
||||
}
|
||||
}
|
||||
string res = "";
|
||||
foreach (string t in dictionary) {
|
||||
bool match = true;
|
||||
int j = 0;
|
||||
for (int i = 0; i < t.Length; ++i) {
|
||||
if (f[j, t[i] - 'a'] == m) {
|
||||
match = false;
|
||||
break;
|
||||
}
|
||||
j = f[j, t[i] - 'a'] + 1;
|
||||
}
|
||||
if (match) {
|
||||
if (t.Length > res.Length || (t.Length == res.Length && t.CompareTo(res) < 0)) {
|
||||
res = t;
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol3-Golang]
|
||||
|
||||
```go
|
||||
func findLongestWord(s string, dictionary []string) (ans string) {
|
||||
m := len(s)
|
||||
f := make([][26]int, m+1)
|
||||
for i := range f[m] {
|
||||
f[m][i] = m
|
||||
}
|
||||
for i := m - 1; i >= 0; i-- {
|
||||
f[i] = f[i+1]
|
||||
f[i][s[i]-'a'] = i
|
||||
}
|
||||
|
||||
outer:
|
||||
for _, t := range dictionary {
|
||||
j := 0
|
||||
for _, ch := range t {
|
||||
if f[j][ch-'a'] == m {
|
||||
continue outer
|
||||
}
|
||||
j = f[j][ch-'a'] + 1
|
||||
}
|
||||
if len(t) > len(ans) || len(t) == len(ans) && t < ans {
|
||||
ans = t
|
||||
}
|
||||
}
|
||||
return
|
||||
}
|
||||
```
|
||||
|
||||
* [sol3-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var findLongestWord = function(s, dictionary) {
|
||||
const m = s.length;
|
||||
const f = new Array(m + 1).fill(0).map(() => new Array(26).fill(m));
|
||||
|
||||
for (let i = m - 1; i >= 0; --i) {
|
||||
for (let j = 0; j < 26; ++j) {
|
||||
if (s[i] === String.fromCharCode('a'.charCodeAt() + j)) {
|
||||
f[i][j] = i;
|
||||
} else {
|
||||
f[i][j] = f[i + 1][j];
|
||||
}
|
||||
}
|
||||
}
|
||||
let res = "";
|
||||
for (const t of dictionary) {
|
||||
let match = true;
|
||||
let j = 0;
|
||||
for (let i = 0; i < t.length; ++i) {
|
||||
if (f[j][t[i].charCodeAt() - 'a'.charCodeAt()] === m) {
|
||||
match = false;
|
||||
break;
|
||||
}
|
||||
j = f[j][t[i].charCodeAt() - 'a'.charCodeAt()] + 1;
|
||||
}
|
||||
if (match) {
|
||||
if (t.length > res.length || (t.length === res.length && t.localeCompare(res) < 0)) {
|
||||
res = t;
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(m \times |\Sigma|+d \times n)$,其中 $d$ 表示 $\textit{dictionary}$ 的长度,$\Sigma$ 为字符集,在本题中字符串只包含英文小写字母,故 $|\Sigma|=26$;$m$ 表示字符串 $s$ 的长度,$n$ 表示 $\textit{dictionary}$ 中字符串的平均长度。预处理的时间复杂度为 $O(m \times |\Sigma|)$;判断 $d$ 个字符串是否为 $s$ 的子序列的事件复杂度为 $O(d \times n)$。
|
||||
|
||||
- 空间复杂度:$O(m \times |\Sigma|)$,为动态规划数组的开销。
|
||||
|
||||
@ -0,0 +1,362 @@
|
||||
#### 方法一:动态规划
|
||||
|
||||
**思路与算法**
|
||||
|
||||
题目的要求等价于「选出最多数量的区间,使得它们互不重叠」。由于选出的区间互不重叠,因此我们可以将它们按照端点从小到大的顺序进行排序,并且无论我们按照左端点还是右端点进行排序,得到的结果都是唯一的。
|
||||
|
||||
这样一来,我们可以先将所有的 $n$ 个区间按照左端点(或者右端点)从小到大进行排序,随后使用动态规划的方法求出区间数量的最大值。设排完序后这 $n$ 个区间的左右端点分别为 $l_0, \cdots, l_{n-1}$ 以及 $r_0, \cdots, r_{n-1}$,那么我们令 $f_i$ 表示「以区间 $i$ 为最后一个区间,可以选出的区间数量的最大值」,状态转移方程即为:
|
||||
|
||||
$$
|
||||
f_i = \max_{j < i ~\wedge~ r_j \leq l_i} \{ f_j \} + 1
|
||||
$$
|
||||
|
||||
即我们枚举倒数第二个区间的编号 $j$,满足 $j < i$,并且第 $j$ 个区间必须要与第 $i$ 个区间不重叠。由于我们已经按照左端点进行升序排序了,因此只要第 $j$ 个区间的右端点 $r_j$ 没有越过第 $i$ 个区间的左端点 $l_i$,即 $r_j \leq l_i$,那么第 $j$ 个区间就与第 $i$ 个区间不重叠。我们在所有满足要求的 $j$ 中,选择 $f_j$ 最大的那一个进行状态转移,如果找不到满足要求的区间,那么状态转移方程中 $\min$ 这一项就为 $0$,$f_i$ 就为 $1$。
|
||||
|
||||
最终的答案即为所有 $f_i$ 中的最大值。
|
||||
|
||||
**代码**
|
||||
|
||||
由于方法一的时间复杂度较高,因此在下面的 $\texttt{Python}$ 代码中,我们尽量使用列表推导优化常数,使得其可以在时间限制内通过所有测试数据。
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
|
||||
if (intervals.empty()) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
sort(intervals.begin(), intervals.end(), [](const auto& u, const auto& v) {
|
||||
return u[0] < v[0];
|
||||
});
|
||||
|
||||
int n = intervals.size();
|
||||
vector<int> f(n, 1);
|
||||
for (int i = 1; i < n; ++i) {
|
||||
for (int j = 0; j < i; ++j) {
|
||||
if (intervals[j][1] <= intervals[i][0]) {
|
||||
f[i] = max(f[i], f[j] + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
return n - *max_element(f.begin(), f.end());
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int eraseOverlapIntervals(int[][] intervals) {
|
||||
if (intervals.length == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
Arrays.sort(intervals, new Comparator<int[]>() {
|
||||
public int compare(int[] interval1, int[] interval2) {
|
||||
return interval1[0] - interval2[0];
|
||||
}
|
||||
});
|
||||
|
||||
int n = intervals.length;
|
||||
int[] f = new int[n];
|
||||
Arrays.fill(f, 1);
|
||||
for (int i = 1; i < n; ++i) {
|
||||
for (int j = 0; j < i; ++j) {
|
||||
if (intervals[j][1] <= intervals[i][0]) {
|
||||
f[i] = Math.max(f[i], f[j] + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
return n - Arrays.stream(f).max().getAsInt();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
|
||||
if not intervals:
|
||||
return 0
|
||||
|
||||
intervals.sort()
|
||||
n = len(intervals)
|
||||
f = [1]
|
||||
|
||||
for i in range(1, n):
|
||||
f.append(max((f[j] for j in range(i) if intervals[j][1] <= intervals[i][0]), default=0) + 1)
|
||||
|
||||
return n - max(f)
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func eraseOverlapIntervals(intervals [][]int) int {
|
||||
n := len(intervals)
|
||||
if n == 0 {
|
||||
return 0
|
||||
}
|
||||
sort.Slice(intervals, func(i, j int) bool { return intervals[i][0] < intervals[j][0] })
|
||||
dp := make([]int, n)
|
||||
for i := range dp {
|
||||
dp[i] = 1
|
||||
}
|
||||
for i := 1; i < n; i++ {
|
||||
for j := 0; j < i; j++ {
|
||||
if intervals[j][1] <= intervals[i][0] {
|
||||
dp[i] = max(dp[i], dp[j]+1)
|
||||
}
|
||||
}
|
||||
}
|
||||
return n - max(dp...)
|
||||
}
|
||||
|
||||
func max(a ...int) int {
|
||||
res := a[0]
|
||||
for _, v := range a[1:] {
|
||||
if v > res {
|
||||
res = v
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
int cmp(int** a, int** b) {
|
||||
return (*a)[0] - (*b)[0];
|
||||
}
|
||||
|
||||
int eraseOverlapIntervals(int** intervals, int intervalsSize, int* intervalsColSize) {
|
||||
if (intervalsSize == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
qsort(intervals, intervalsSize, sizeof(int*), cmp);
|
||||
int f[intervalsSize];
|
||||
for (int i = 0; i < intervalsSize; i++) {
|
||||
f[i] = 1;
|
||||
}
|
||||
int maxn = 1;
|
||||
for (int i = 1; i < intervalsSize; ++i) {
|
||||
for (int j = 0; j < i; ++j) {
|
||||
if (intervals[j][1] <= intervals[i][0]) {
|
||||
f[i] = fmax(f[i], f[j] + 1);
|
||||
}
|
||||
}
|
||||
maxn = fmax(maxn, f[i]);
|
||||
}
|
||||
return intervalsSize - maxn;
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var eraseOverlapIntervals = function(intervals) {
|
||||
if (!intervals.length) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
intervals.sort((a, b) => a[0] - b[0]);
|
||||
const n = intervals.length;
|
||||
const f = new Array(n).fill(1);
|
||||
|
||||
for (let i = 1; i < n; i++) {
|
||||
for (let j = 0; j < i; j++) {
|
||||
if (intervals[j][1] <= intervals[i][0]) {
|
||||
f[i] = Math.max(f[i], f[j] + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
return n - Math.max(...f);
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n^2)$,其中 $n$ 是区间的数量。我们需要 $O(n \log n)$ 的时间对所有的区间按照左端点进行升序排序,并且需要 $O(n^2)$ 的时间进行动态规划。由于前者在渐进意义下小于后者,因此总时间复杂度为 $O(n^2)$。
|
||||
|
||||
注意到方法一本质上是一个「最长上升子序列」问题,因此我们可以将时间复杂度优化至 $O(n \log n)$,具体可以参考「[300. 最长递增子序列的官方题解](https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-by-leetcode-soluti/)」。
|
||||
|
||||
- 空间复杂度:$O(n)$,即为存储所有状态 $f_i$ 需要的空间。
|
||||
|
||||
#### 方法二:贪心
|
||||
|
||||
**思路与算法**
|
||||
|
||||
我们不妨想一想应该选择哪一个区间作为首个区间。
|
||||
|
||||
假设在某一种**最优**的选择方法中,$[l_k, r_k]$ 是首个(即最左侧的)区间,那么它的左侧没有其它区间,右侧有若干个不重叠的区间。设想一下,如果此时存在一个区间 $[l_j, r_j]$,使得 $r_j < r_k$,即区间 $j$ 的右端点在区间 $k$ 的左侧,那么我们将区间 $k$ 替换为区间 $j$,其与剩余右侧被选择的区间仍然是不重叠的。而当我们将区间 $k$ 替换为区间 $j$ 后,就得到了另一种**最优**的选择方法。
|
||||
|
||||
我们可以不断地寻找右端点在首个区间右端点左侧的新区间,将首个区间替换成该区间。那么当我们无法替换时,**首个区间就是所有可以选择的区间中右端点最小的那个区间**。因此我们将所有区间按照右端点从小到大进行排序,那么排完序之后的首个区间,就是我们选择的首个区间。
|
||||
|
||||
如果有多个区间的右端点都同样最小怎么办?由于我们选择的是首个区间,因此在左侧不会有其它的区间,那么左端点在何处是不重要的,我们只要任意选择一个右端点最小的区间即可。
|
||||
|
||||
当确定了首个区间之后,所有与首个区间不重合的区间就组成了一个规模更小的子问题。由于我们已经在初始时将所有区间按照右端点排好序了,因此对于这个子问题,我们无需再次进行排序,只要找出其中**与首个区间不重合**并且右端点最小的区间即可。用相同的方法,我们可以依次确定后续的所有区间。
|
||||
|
||||
在实际的代码编写中,我们对按照右端点排好序的区间进行遍历,并且实时维护上一个选择区间的右端点 $\textit{right}$。如果当前遍历到的区间 $[l_i, r_i]$ 与上一个区间不重合,即 $l_i \geq \textit{right}$,那么我们就可以贪心地选择这个区间,并将 $\textit{right}$ 更新为 $r_i$。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol2-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
|
||||
if (intervals.empty()) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
sort(intervals.begin(), intervals.end(), [](const auto& u, const auto& v) {
|
||||
return u[1] < v[1];
|
||||
});
|
||||
|
||||
int n = intervals.size();
|
||||
int right = intervals[0][1];
|
||||
int ans = 1;
|
||||
for (int i = 1; i < n; ++i) {
|
||||
if (intervals[i][0] >= right) {
|
||||
++ans;
|
||||
right = intervals[i][1];
|
||||
}
|
||||
}
|
||||
return n - ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int eraseOverlapIntervals(int[][] intervals) {
|
||||
if (intervals.length == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
Arrays.sort(intervals, new Comparator<int[]>() {
|
||||
public int compare(int[] interval1, int[] interval2) {
|
||||
return interval1[1] - interval2[1];
|
||||
}
|
||||
});
|
||||
|
||||
int n = intervals.length;
|
||||
int right = intervals[0][1];
|
||||
int ans = 1;
|
||||
for (int i = 1; i < n; ++i) {
|
||||
if (intervals[i][0] >= right) {
|
||||
++ans;
|
||||
right = intervals[i][1];
|
||||
}
|
||||
}
|
||||
return n - ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
|
||||
if not intervals:
|
||||
return 0
|
||||
|
||||
intervals.sort(key=lambda x: x[1])
|
||||
n = len(intervals)
|
||||
right = intervals[0][1]
|
||||
ans = 1
|
||||
|
||||
for i in range(1, n):
|
||||
if intervals[i][0] >= right:
|
||||
ans += 1
|
||||
right = intervals[i][1]
|
||||
|
||||
return n - ans
|
||||
```
|
||||
|
||||
* [sol2-Golang]
|
||||
|
||||
```go
|
||||
func eraseOverlapIntervals(intervals [][]int) int {
|
||||
n := len(intervals)
|
||||
if n == 0 {
|
||||
return 0
|
||||
}
|
||||
sort.Slice(intervals, func(i, j int) bool { return intervals[i][1] < intervals[j][1] })
|
||||
ans, right := 1, intervals[0][1]
|
||||
for _, p := range intervals[1:] {
|
||||
if p[0] >= right {
|
||||
ans++
|
||||
right = p[1]
|
||||
}
|
||||
}
|
||||
return n - ans
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-C]
|
||||
|
||||
```C
|
||||
int cmp(int** a, int** b) {
|
||||
return (*a)[1] - (*b)[1];
|
||||
}
|
||||
|
||||
int eraseOverlapIntervals(int** intervals, int intervalsSize, int* intervalsColSize) {
|
||||
if (intervalsSize == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
qsort(intervals, intervalsSize, sizeof(int*), cmp);
|
||||
|
||||
int right = intervals[0][1];
|
||||
int ans = 1;
|
||||
for (int i = 1; i < intervalsSize; ++i) {
|
||||
if (intervals[i][0] >= right) {
|
||||
++ans;
|
||||
right = intervals[i][1];
|
||||
}
|
||||
}
|
||||
return intervalsSize - ans;
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var eraseOverlapIntervals = function(intervals) {
|
||||
if (!intervals.length) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
intervals.sort((a, b) => a[1] - b[1]);
|
||||
|
||||
const n = intervals.length;
|
||||
let right = intervals[0][1];
|
||||
let ans = 1;
|
||||
for (let i = 1; i < n; ++i) {
|
||||
if (intervals[i][0] >= right) {
|
||||
++ans;
|
||||
right = intervals[i][1];
|
||||
}
|
||||
}
|
||||
return n - ans;
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n \log n)$,其中 $n$ 是区间的数量。我们需要 $O(n \log n)$ 的时间对所有的区间按照右端点进行升序排序,并且需要 $O(n)$ 的时间进行遍历。由于前者在渐进意义下大于后者,因此总时间复杂度为 $O(n \log n)$。
|
||||
|
||||
- 空间复杂度:$O(\log n)$,即为排序需要使用的栈空间。
|
||||
|
||||
@ -0,0 +1,140 @@
|
||||
#### 方法一:深度优先搜索【通过】
|
||||
|
||||
**思路**
|
||||
|
||||
序列化二叉树。
|
||||
|
||||
* [snippet1-Python]
|
||||
|
||||
```python
|
||||
1
|
||||
/ \
|
||||
2 3
|
||||
/ \
|
||||
4 5
|
||||
```
|
||||
|
||||
例如上面这棵树序列化结果为 `1,2,#,#,3,4,#,#,5,#,#`。每棵不同子树的序列化结果都是唯一的。
|
||||
|
||||
**算法**
|
||||
|
||||
使用深度优先搜索,其中递归函数返回当前子树的序列化结果。把每个节点开始的子树序列化结果保存在 $map$ 中,然后判断是否存在重复的子树。
|
||||
|
||||
* [solution1-Python]
|
||||
|
||||
```python
|
||||
class Solution(object):
|
||||
def findDuplicateSubtrees(self, root):
|
||||
count = collections.Counter()
|
||||
ans = []
|
||||
def collect(node):
|
||||
if not node: return "#"
|
||||
serial = "{},{},{}".format(node.val, collect(node.left), collect(node.right))
|
||||
count[serial] += 1
|
||||
if count[serial] == 2:
|
||||
ans.append(node)
|
||||
return serial
|
||||
|
||||
collect(root)
|
||||
return ans
|
||||
```
|
||||
|
||||
* [solution1-Java]
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
Map<String, Integer> count;
|
||||
List<TreeNode> ans;
|
||||
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
|
||||
count = new HashMap();
|
||||
ans = new ArrayList();
|
||||
collect(root);
|
||||
return ans;
|
||||
}
|
||||
|
||||
public String collect(TreeNode node) {
|
||||
if (node == null) return "#";
|
||||
String serial = node.val + "," + collect(node.left) + "," + collect(node.right);
|
||||
count.put(serial, count.getOrDefault(serial, 0) + 1);
|
||||
if (count.get(serial) == 2)
|
||||
ans.add(node);
|
||||
return serial;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
* 时间复杂度:$O(N^2)$,其中 $N$ 是二叉树上节点的数量。遍历所有节点,在每个节点处序列化需要时间 $O(N)$。
|
||||
|
||||
* 空间复杂度:$O(N^2)$,`count` 的大小。
|
||||
|
||||
#### 方法二:唯一标识符【通过】
|
||||
|
||||
**思路**
|
||||
|
||||
假设每棵子树都有一个唯一标识符:只有当两个子树的 id 相同时,认为这两个子树是相同的。
|
||||
|
||||
一个节点 `node` 的左孩子 id 为 `x`,右孩子 id 为 `y`,那么该节点的 id 为 `(node.val, x, y)`。
|
||||
|
||||
**算法**
|
||||
|
||||
如果三元组 `(node.val, x, y)` 第一次出现,则创建一个这样的三元组记录该子树。如果已经出现过,则直接使用该子树对应的 id。
|
||||
|
||||
* [solution2-Python]
|
||||
|
||||
```python
|
||||
class Solution(object):
|
||||
def findDuplicateSubtrees(self, root):
|
||||
trees = collections.defaultdict()
|
||||
trees.default_factory = trees.__len__
|
||||
count = collections.Counter()
|
||||
ans = []
|
||||
def lookup(node):
|
||||
if node:
|
||||
uid = trees[node.val, lookup(node.left), lookup(node.right)]
|
||||
count[uid] += 1
|
||||
if count[uid] == 2:
|
||||
ans.append(node)
|
||||
return uid
|
||||
|
||||
lookup(root)
|
||||
return ans
|
||||
```
|
||||
|
||||
* [solution2-Java]
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
int t;
|
||||
Map<String, Integer> trees;
|
||||
Map<Integer, Integer> count;
|
||||
List<TreeNode> ans;
|
||||
|
||||
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
|
||||
t = 1;
|
||||
trees = new HashMap();
|
||||
count = new HashMap();
|
||||
ans = new ArrayList();
|
||||
lookup(root);
|
||||
return ans;
|
||||
}
|
||||
|
||||
public int lookup(TreeNode node) {
|
||||
if (node == null) return 0;
|
||||
String serial = node.val + "," + lookup(node.left) + "," + lookup(node.right);
|
||||
int uid = trees.computeIfAbsent(serial, x-> t++);
|
||||
count.put(uid, count.getOrDefault(uid, 0) + 1);
|
||||
if (count.get(uid) == 2)
|
||||
ans.add(node);
|
||||
return uid;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
* 时间复杂度:$O(N)$,其中 $N$ 二叉树上节点的数量,每个节点都需要访问一次。
|
||||
|
||||
* 空间复杂度:$O(N)$,每棵子树的存储空间都为 $O(1)$。
|
||||
|
||||
@ -0,0 +1,797 @@
|
||||
#### 方法一:确定有限状态自动机
|
||||
|
||||
**预备知识**
|
||||
|
||||
确定有限状态自动机(以下简称「自动机」)是一类计算模型。它包含一系列状态,这些状态中:
|
||||
|
||||
- 有一个特殊的状态,被称作「初始状态」。
|
||||
- 还有一系列状态被称为「接受状态」,它们组成了一个特殊的集合。其中,一个状态可能既是「初始状态」,也是「接受状态」。
|
||||
|
||||
起初,这个自动机处于「初始状态」。随后,它顺序地读取字符串中的每一个字符,并根据当前状态和读入的字符,按照某个事先约定好的「转移规则」,从当前状态转移到下一个状态;当状态转移完成后,它就读取下一个字符。当字符串全部读取完毕后,如果自动机处于某个「接受状态」,则判定该字符串「被接受」;否则,判定该字符串「被拒绝」。
|
||||
|
||||
**注意**:如果输入的过程中某一步转移失败了,即不存在对应的「转移规则」,此时计算将提前中止。在这种情况下我们也判定该字符串「被拒绝」。
|
||||
|
||||
一个自动机,总能够回答某种形式的「对于给定的输入字符串 S,判断其是否满足条件 P」的问题。在本题中,条件 P 即为「构成合法的表示数值的字符串」。
|
||||
|
||||
自动机驱动的编程,可以被看做一种暴力枚举方法的延伸:它穷尽了在任何一种情况下,对应任何的输入,需要做的事情。
|
||||
|
||||
自动机在计算机科学领域有着广泛的应用。在算法领域,它与大名鼎鼎的字符串查找算法「KMP 算法」有着密切的关联;在工程领域,它是实现「正则表达式」的基础。
|
||||
|
||||
**问题描述**
|
||||
|
||||
在 [C++ 文档](https://en.cppreference.com/w/cpp/language/floating_literal) 中,描述了一个合法的数值字符串应当具有的格式。具体而言,它包含以下部分:
|
||||
- 符号位,即 $+$、$-$ 两种符号
|
||||
- 整数部分,即由若干字符 $0-9$ 组成的字符串
|
||||
- 小数点
|
||||
- 小数部分,其构成与整数部分相同
|
||||
- 指数部分,其中包含开头的字符 $\text{e}$(大写小写均可)、可选的符号位,和整数部分
|
||||
|
||||
在上面描述的五个部分中,每个部分都不是必需的,但也受一些额外规则的制约,如:
|
||||
- 如果符号位存在,其后面必须跟着数字或小数点。
|
||||
- 小数点的前后两侧,至少有一侧是数字。
|
||||
|
||||
**思路与算法**
|
||||
|
||||
根据上面的描述,现在可以定义自动机的「状态集合」了。那么怎么挖掘出所有可能的状态呢?一个常用的技巧是,用「当前处理到字符串的哪个部分」当作状态的表述。根据这一技巧,不难挖掘出所有状态:
|
||||
|
||||
0. 初始状态
|
||||
1. 符号位
|
||||
2. 整数部分
|
||||
3. 左侧有整数的小数点
|
||||
4. 左侧无整数的小数点(根据前面的第二条额外规则,需要对左侧有无整数的两种小数点做区分)
|
||||
5. 小数部分
|
||||
6. 字符 $\text{e}$
|
||||
7. 指数部分的符号位
|
||||
8. 指数部分的整数部分
|
||||
|
||||
下一步是找出「初始状态」和「接受状态」的集合。根据题意,「初始状态」应当为状态 0,而「接受状态」的集合则为状态 2、状态 3、状态 5 以及状态 8。换言之,字符串的末尾要么是空格,要么是数字,要么是小数点,但前提是小数点的前面有数字。
|
||||
|
||||
最后,需要定义「转移规则」。结合数值字符串应当具备的格式,将自动机转移的过程以图解的方式表示出来:
|
||||
|
||||
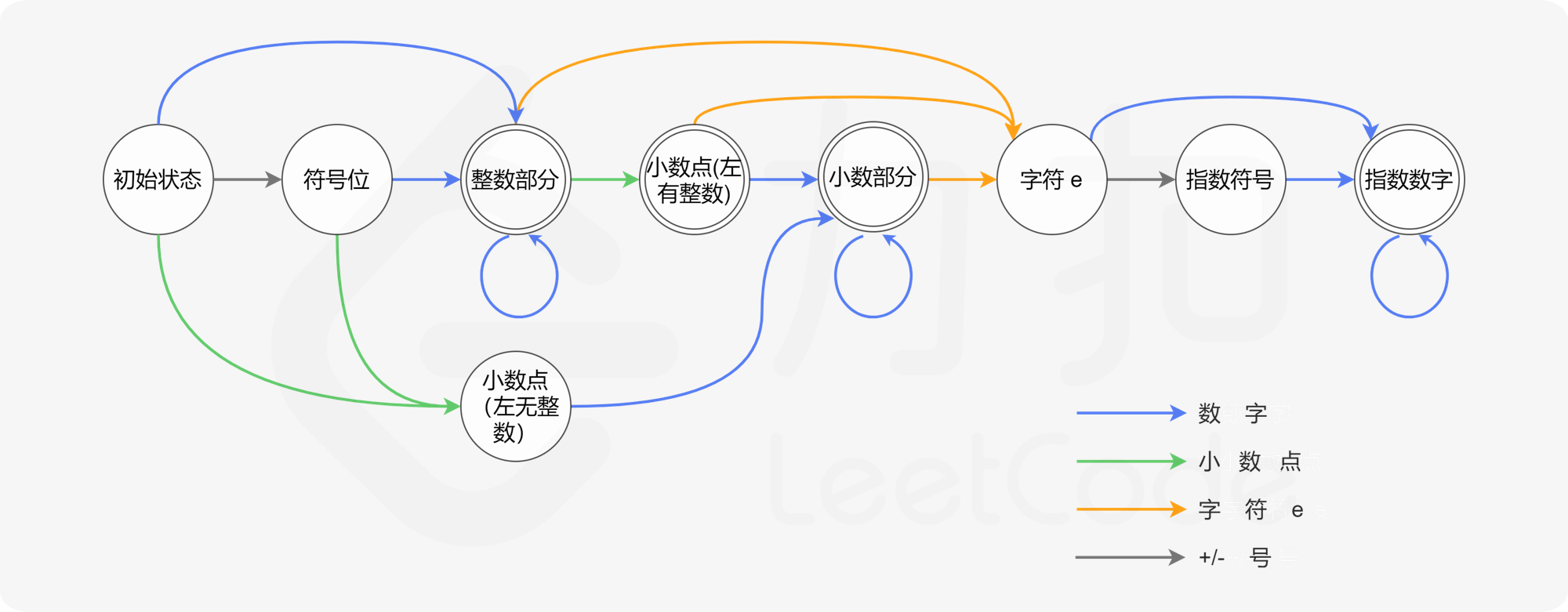
|
||||
|
||||
比较上图与「预备知识」一节中对自动机的描述,可以看出有一点不同:
|
||||
- 我们没有单独地考虑每种字符,而是划分为若干类。由于全部 $10$ 个数字字符彼此之间都等价,因此只需定义一种统一的「数字」类型即可。对于正负号也是同理。
|
||||
|
||||
在实际代码中,我们需要处理转移失败的情况。为了处理这种情况,我们可以创建一个特殊的拒绝状态。如果当前状态下没有对应读入字符的「转移规则」,我们就转移到这个特殊的拒绝状态。一旦自动机转移到这个特殊状态,我们就可以立即判定该字符串不「被接受」。
|
||||
|
||||
**代码**
|
||||
|
||||
可以很简单地将上面的状态转移图翻译成代码:
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
enum State {
|
||||
STATE_INITIAL,
|
||||
STATE_INT_SIGN,
|
||||
STATE_INTEGER,
|
||||
STATE_POINT,
|
||||
STATE_POINT_WITHOUT_INT,
|
||||
STATE_FRACTION,
|
||||
STATE_EXP,
|
||||
STATE_EXP_SIGN,
|
||||
STATE_EXP_NUMBER,
|
||||
STATE_END
|
||||
};
|
||||
|
||||
enum CharType {
|
||||
CHAR_NUMBER,
|
||||
CHAR_EXP,
|
||||
CHAR_POINT,
|
||||
CHAR_SIGN,
|
||||
CHAR_ILLEGAL
|
||||
};
|
||||
|
||||
CharType toCharType(char ch) {
|
||||
if (ch >= '0' && ch <= '9') {
|
||||
return CHAR_NUMBER;
|
||||
} else if (ch == 'e' || ch == 'E') {
|
||||
return CHAR_EXP;
|
||||
} else if (ch == '.') {
|
||||
return CHAR_POINT;
|
||||
} else if (ch == '+' || ch == '-') {
|
||||
return CHAR_SIGN;
|
||||
} else {
|
||||
return CHAR_ILLEGAL;
|
||||
}
|
||||
}
|
||||
|
||||
bool isNumber(string s) {
|
||||
unordered_map<State, unordered_map<CharType, State>> transfer{
|
||||
{
|
||||
STATE_INITIAL, {
|
||||
{CHAR_NUMBER, STATE_INTEGER},
|
||||
{CHAR_POINT, STATE_POINT_WITHOUT_INT},
|
||||
{CHAR_SIGN, STATE_INT_SIGN}
|
||||
}
|
||||
}, {
|
||||
STATE_INT_SIGN, {
|
||||
{CHAR_NUMBER, STATE_INTEGER},
|
||||
{CHAR_POINT, STATE_POINT_WITHOUT_INT}
|
||||
}
|
||||
}, {
|
||||
STATE_INTEGER, {
|
||||
{CHAR_NUMBER, STATE_INTEGER},
|
||||
{CHAR_EXP, STATE_EXP},
|
||||
{CHAR_POINT, STATE_POINT}
|
||||
}
|
||||
}, {
|
||||
STATE_POINT, {
|
||||
{CHAR_NUMBER, STATE_FRACTION},
|
||||
{CHAR_EXP, STATE_EXP}
|
||||
}
|
||||
}, {
|
||||
STATE_POINT_WITHOUT_INT, {
|
||||
{CHAR_NUMBER, STATE_FRACTION}
|
||||
}
|
||||
}, {
|
||||
STATE_FRACTION,
|
||||
{
|
||||
{CHAR_NUMBER, STATE_FRACTION},
|
||||
{CHAR_EXP, STATE_EXP}
|
||||
}
|
||||
}, {
|
||||
STATE_EXP,
|
||||
{
|
||||
{CHAR_NUMBER, STATE_EXP_NUMBER},
|
||||
{CHAR_SIGN, STATE_EXP_SIGN}
|
||||
}
|
||||
}, {
|
||||
STATE_EXP_SIGN, {
|
||||
{CHAR_NUMBER, STATE_EXP_NUMBER}
|
||||
}
|
||||
}, {
|
||||
STATE_EXP_NUMBER, {
|
||||
{CHAR_NUMBER, STATE_EXP_NUMBER}
|
||||
}
|
||||
}
|
||||
};
|
||||
|
||||
int len = s.length();
|
||||
State st = STATE_INITIAL;
|
||||
|
||||
for (int i = 0; i < len; i++) {
|
||||
CharType typ = toCharType(s[i]);
|
||||
if (transfer[st].find(typ) == transfer[st].end()) {
|
||||
return false;
|
||||
} else {
|
||||
st = transfer[st][typ];
|
||||
}
|
||||
}
|
||||
return st == STATE_INTEGER || st == STATE_POINT || st == STATE_FRACTION || st == STATE_EXP_NUMBER || st == STATE_END;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public boolean isNumber(String s) {
|
||||
Map<State, Map<CharType, State>> transfer = new HashMap<State, Map<CharType, State>>();
|
||||
Map<CharType, State> initialMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
|
||||
put(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT);
|
||||
put(CharType.CHAR_SIGN, State.STATE_INT_SIGN);
|
||||
}};
|
||||
transfer.put(State.STATE_INITIAL, initialMap);
|
||||
Map<CharType, State> intSignMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
|
||||
put(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT);
|
||||
}};
|
||||
transfer.put(State.STATE_INT_SIGN, intSignMap);
|
||||
Map<CharType, State> integerMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
|
||||
put(CharType.CHAR_EXP, State.STATE_EXP);
|
||||
put(CharType.CHAR_POINT, State.STATE_POINT);
|
||||
}};
|
||||
transfer.put(State.STATE_INTEGER, integerMap);
|
||||
Map<CharType, State> pointMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
|
||||
put(CharType.CHAR_EXP, State.STATE_EXP);
|
||||
}};
|
||||
transfer.put(State.STATE_POINT, pointMap);
|
||||
Map<CharType, State> pointWithoutIntMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
|
||||
}};
|
||||
transfer.put(State.STATE_POINT_WITHOUT_INT, pointWithoutIntMap);
|
||||
Map<CharType, State> fractionMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
|
||||
put(CharType.CHAR_EXP, State.STATE_EXP);
|
||||
}};
|
||||
transfer.put(State.STATE_FRACTION, fractionMap);
|
||||
Map<CharType, State> expMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
|
||||
put(CharType.CHAR_SIGN, State.STATE_EXP_SIGN);
|
||||
}};
|
||||
transfer.put(State.STATE_EXP, expMap);
|
||||
Map<CharType, State> expSignMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
|
||||
}};
|
||||
transfer.put(State.STATE_EXP_SIGN, expSignMap);
|
||||
Map<CharType, State> expNumberMap = new HashMap<CharType, State>() {{
|
||||
put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
|
||||
}};
|
||||
transfer.put(State.STATE_EXP_NUMBER, expNumberMap);
|
||||
|
||||
int length = s.length();
|
||||
State state = State.STATE_INITIAL;
|
||||
|
||||
for (int i = 0; i < length; i++) {
|
||||
CharType type = toCharType(s.charAt(i));
|
||||
if (!transfer.get(state).containsKey(type)) {
|
||||
return false;
|
||||
} else {
|
||||
state = transfer.get(state).get(type);
|
||||
}
|
||||
}
|
||||
return state == State.STATE_INTEGER || state == State.STATE_POINT || state == State.STATE_FRACTION || state == State.STATE_EXP_NUMBER || state == State.STATE_END;
|
||||
}
|
||||
|
||||
public CharType toCharType(char ch) {
|
||||
if (ch >= '0' && ch <= '9') {
|
||||
return CharType.CHAR_NUMBER;
|
||||
} else if (ch == 'e' || ch == 'E') {
|
||||
return CharType.CHAR_EXP;
|
||||
} else if (ch == '.') {
|
||||
return CharType.CHAR_POINT;
|
||||
} else if (ch == '+' || ch == '-') {
|
||||
return CharType.CHAR_SIGN;
|
||||
} else {
|
||||
return CharType.CHAR_ILLEGAL;
|
||||
}
|
||||
}
|
||||
|
||||
enum State {
|
||||
STATE_INITIAL,
|
||||
STATE_INT_SIGN,
|
||||
STATE_INTEGER,
|
||||
STATE_POINT,
|
||||
STATE_POINT_WITHOUT_INT,
|
||||
STATE_FRACTION,
|
||||
STATE_EXP,
|
||||
STATE_EXP_SIGN,
|
||||
STATE_EXP_NUMBER,
|
||||
STATE_END
|
||||
}
|
||||
|
||||
enum CharType {
|
||||
CHAR_NUMBER,
|
||||
CHAR_EXP,
|
||||
CHAR_POINT,
|
||||
CHAR_SIGN,
|
||||
CHAR_ILLEGAL
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
public bool IsNumber(string s) {
|
||||
Dictionary<State, Dictionary<CharType, State>> transfer = new Dictionary<State, Dictionary<CharType, State>>();
|
||||
Dictionary<CharType, State> initialDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_INTEGER},
|
||||
{CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT},
|
||||
{CharType.CHAR_SIGN, State.STATE_INT_SIGN}
|
||||
};
|
||||
transfer.Add(State.STATE_INITIAL, initialDictionary);
|
||||
Dictionary<CharType, State> intSignDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_INTEGER},
|
||||
{CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT}
|
||||
};
|
||||
transfer.Add(State.STATE_INT_SIGN, intSignDictionary);
|
||||
Dictionary<CharType, State> integerDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_INTEGER},
|
||||
{CharType.CHAR_EXP, State.STATE_EXP},
|
||||
{CharType.CHAR_POINT, State.STATE_POINT}
|
||||
};
|
||||
transfer.Add(State.STATE_INTEGER, integerDictionary);
|
||||
Dictionary<CharType, State> pointDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_FRACTION},
|
||||
{CharType.CHAR_EXP, State.STATE_EXP}
|
||||
};
|
||||
transfer.Add(State.STATE_POINT, pointDictionary);
|
||||
Dictionary<CharType, State> pointWithoutIntDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_FRACTION}
|
||||
};
|
||||
transfer.Add(State.STATE_POINT_WITHOUT_INT, pointWithoutIntDictionary);
|
||||
Dictionary<CharType, State> fractionDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_FRACTION},
|
||||
{CharType.CHAR_EXP, State.STATE_EXP}
|
||||
};
|
||||
transfer.Add(State.STATE_FRACTION, fractionDictionary);
|
||||
Dictionary<CharType, State> expDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER},
|
||||
{CharType.CHAR_SIGN, State.STATE_EXP_SIGN}
|
||||
};
|
||||
transfer.Add(State.STATE_EXP, expDictionary);
|
||||
Dictionary<CharType, State> expSignDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER}
|
||||
};
|
||||
transfer.Add(State.STATE_EXP_SIGN, expSignDictionary);
|
||||
Dictionary<CharType, State> expNumberDictionary = new Dictionary<CharType, State> {
|
||||
{CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER}
|
||||
};
|
||||
transfer.Add(State.STATE_EXP_NUMBER, expNumberDictionary);
|
||||
|
||||
int length = s.Length;
|
||||
State state = State.STATE_INITIAL;
|
||||
|
||||
for (int i = 0; i < length; i++) {
|
||||
CharType type = ToCharType(s[i]);
|
||||
if (!transfer[state].ContainsKey(type)) {
|
||||
return false;
|
||||
} else {
|
||||
state = transfer[state][type];
|
||||
}
|
||||
}
|
||||
return state == State.STATE_INTEGER || state == State.STATE_POINT || state == State.STATE_FRACTION || state == State.STATE_EXP_NUMBER || state == State.STATE_END;
|
||||
}
|
||||
|
||||
CharType ToCharType(char ch) {
|
||||
if (ch >= '0' && ch <= '9') {
|
||||
return CharType.CHAR_NUMBER;
|
||||
} else if (ch == 'e' || ch == 'E') {
|
||||
return CharType.CHAR_EXP;
|
||||
} else if (ch == '.') {
|
||||
return CharType.CHAR_POINT;
|
||||
} else if (ch == '+' || ch == '-') {
|
||||
return CharType.CHAR_SIGN;
|
||||
} else {
|
||||
return CharType.CHAR_ILLEGAL;
|
||||
}
|
||||
}
|
||||
|
||||
enum State {
|
||||
STATE_INITIAL,
|
||||
STATE_INT_SIGN,
|
||||
STATE_INTEGER,
|
||||
STATE_POINT,
|
||||
STATE_POINT_WITHOUT_INT,
|
||||
STATE_FRACTION,
|
||||
STATE_EXP,
|
||||
STATE_EXP_SIGN,
|
||||
STATE_EXP_NUMBER,
|
||||
STATE_END
|
||||
}
|
||||
|
||||
enum CharType {
|
||||
CHAR_NUMBER,
|
||||
CHAR_EXP,
|
||||
CHAR_POINT,
|
||||
CHAR_SIGN,
|
||||
CHAR_ILLEGAL
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```golang
|
||||
type State int
|
||||
type CharType int
|
||||
|
||||
const (
|
||||
STATE_INITIAL State = iota
|
||||
STATE_INT_SIGN
|
||||
STATE_INTEGER
|
||||
STATE_POINT
|
||||
STATE_POINT_WITHOUT_INT
|
||||
STATE_FRACTION
|
||||
STATE_EXP
|
||||
STATE_EXP_SIGN
|
||||
STATE_EXP_NUMBER
|
||||
STATE_END
|
||||
)
|
||||
|
||||
const (
|
||||
CHAR_NUMBER CharType = iota
|
||||
CHAR_EXP
|
||||
CHAR_POINT
|
||||
CHAR_SIGN
|
||||
CHAR_ILLEGAL
|
||||
)
|
||||
|
||||
func toCharType(ch byte) CharType {
|
||||
switch ch {
|
||||
case '0', '1', '2', '3', '4', '5', '6', '7', '8', '9':
|
||||
return CHAR_NUMBER
|
||||
case 'e', 'E':
|
||||
return CHAR_EXP
|
||||
case '.':
|
||||
return CHAR_POINT
|
||||
case '+', '-':
|
||||
return CHAR_SIGN
|
||||
default:
|
||||
return CHAR_ILLEGAL
|
||||
}
|
||||
}
|
||||
|
||||
func isNumber(s string) bool {
|
||||
transfer := map[State]map[CharType]State{
|
||||
STATE_INITIAL: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_INTEGER,
|
||||
CHAR_POINT: STATE_POINT_WITHOUT_INT,
|
||||
CHAR_SIGN: STATE_INT_SIGN,
|
||||
},
|
||||
STATE_INT_SIGN: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_INTEGER,
|
||||
CHAR_POINT: STATE_POINT_WITHOUT_INT,
|
||||
},
|
||||
STATE_INTEGER: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_INTEGER,
|
||||
CHAR_EXP: STATE_EXP,
|
||||
CHAR_POINT: STATE_POINT,
|
||||
},
|
||||
STATE_POINT: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_FRACTION,
|
||||
CHAR_EXP: STATE_EXP,
|
||||
},
|
||||
STATE_POINT_WITHOUT_INT: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_FRACTION,
|
||||
},
|
||||
STATE_FRACTION: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_FRACTION,
|
||||
CHAR_EXP: STATE_EXP,
|
||||
},
|
||||
STATE_EXP: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_EXP_NUMBER,
|
||||
CHAR_SIGN: STATE_EXP_SIGN,
|
||||
},
|
||||
STATE_EXP_SIGN: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_EXP_NUMBER,
|
||||
},
|
||||
STATE_EXP_NUMBER: map[CharType]State{
|
||||
CHAR_NUMBER: STATE_EXP_NUMBER,
|
||||
},
|
||||
}
|
||||
state := STATE_INITIAL
|
||||
for i := 0; i < len(s); i++ {
|
||||
typ := toCharType(s[i])
|
||||
if _, ok := transfer[state][typ]; !ok {
|
||||
return false
|
||||
} else {
|
||||
state = transfer[state][typ]
|
||||
}
|
||||
}
|
||||
return state == STATE_INTEGER || state == STATE_POINT || state == STATE_FRACTION || state == STATE_EXP_NUMBER || state == STATE_END
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
enum State {
|
||||
STATE_INITIAL,
|
||||
STATE_INT_SIGN,
|
||||
STATE_INTEGER,
|
||||
STATE_POINT,
|
||||
STATE_POINT_WITHOUT_INT,
|
||||
STATE_FRACTION,
|
||||
STATE_EXP,
|
||||
STATE_EXP_SIGN,
|
||||
STATE_EXP_NUMBER,
|
||||
STATE_END,
|
||||
STATE_ILLEGAL
|
||||
};
|
||||
|
||||
enum CharType {
|
||||
CHAR_NUMBER,
|
||||
CHAR_EXP,
|
||||
CHAR_POINT,
|
||||
CHAR_SIGN,
|
||||
CHAR_ILLEGAL
|
||||
};
|
||||
|
||||
enum CharType toCharType(char ch) {
|
||||
if (ch >= '0' && ch <= '9') {
|
||||
return CHAR_NUMBER;
|
||||
} else if (ch == 'e' || ch == 'E') {
|
||||
return CHAR_EXP;
|
||||
} else if (ch == '.') {
|
||||
return CHAR_POINT;
|
||||
} else if (ch == '+' || ch == '-') {
|
||||
return CHAR_SIGN;
|
||||
} else {
|
||||
return CHAR_ILLEGAL;
|
||||
}
|
||||
}
|
||||
|
||||
enum State transfer(enum State st, enum CharType typ) {
|
||||
switch (st) {
|
||||
case STATE_INITIAL: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_INTEGER;
|
||||
case CHAR_POINT:
|
||||
return STATE_POINT_WITHOUT_INT;
|
||||
case CHAR_SIGN:
|
||||
return STATE_INT_SIGN;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
case STATE_INT_SIGN: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_INTEGER;
|
||||
case CHAR_POINT:
|
||||
return STATE_POINT_WITHOUT_INT;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
case STATE_INTEGER: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_INTEGER;
|
||||
case CHAR_EXP:
|
||||
return STATE_EXP;
|
||||
case CHAR_POINT:
|
||||
return STATE_POINT;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
case STATE_POINT: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_FRACTION;
|
||||
case CHAR_EXP:
|
||||
return STATE_EXP;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
case STATE_POINT_WITHOUT_INT: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_FRACTION;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
case STATE_FRACTION: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_FRACTION;
|
||||
case CHAR_EXP:
|
||||
return STATE_EXP;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
case STATE_EXP: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_EXP_NUMBER;
|
||||
case CHAR_SIGN:
|
||||
return STATE_EXP_SIGN;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
case STATE_EXP_SIGN: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_EXP_NUMBER;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
case STATE_EXP_NUMBER: {
|
||||
switch (typ) {
|
||||
case CHAR_NUMBER:
|
||||
return STATE_EXP_NUMBER;
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
default:
|
||||
return STATE_ILLEGAL;
|
||||
}
|
||||
}
|
||||
|
||||
bool isNumber(char* s) {
|
||||
int len = strlen(s);
|
||||
enum State st = STATE_INITIAL;
|
||||
|
||||
for (int i = 0; i < len; i++) {
|
||||
enum CharType typ = toCharType(s[i]);
|
||||
enum State nextState = transfer(st, typ);
|
||||
if (nextState == STATE_ILLEGAL) return false;
|
||||
st = nextState;
|
||||
}
|
||||
return st == STATE_INTEGER || st == STATE_POINT || st == STATE_FRACTION || st == STATE_EXP_NUMBER || st == STATE_END;
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
from enum import Enum
|
||||
|
||||
class Solution:
|
||||
def isNumber(self, s: str) -> bool:
|
||||
State = Enum("State", [
|
||||
"STATE_INITIAL",
|
||||
"STATE_INT_SIGN",
|
||||
"STATE_INTEGER",
|
||||
"STATE_POINT",
|
||||
"STATE_POINT_WITHOUT_INT",
|
||||
"STATE_FRACTION",
|
||||
"STATE_EXP",
|
||||
"STATE_EXP_SIGN",
|
||||
"STATE_EXP_NUMBER",
|
||||
"STATE_END"
|
||||
])
|
||||
Chartype = Enum("Chartype", [
|
||||
"CHAR_NUMBER",
|
||||
"CHAR_EXP",
|
||||
"CHAR_POINT",
|
||||
"CHAR_SIGN",
|
||||
"CHAR_ILLEGAL"
|
||||
])
|
||||
|
||||
def toChartype(ch: str) -> Chartype:
|
||||
if ch.isdigit():
|
||||
return Chartype.CHAR_NUMBER
|
||||
elif ch.lower() == "e":
|
||||
return Chartype.CHAR_EXP
|
||||
elif ch == ".":
|
||||
return Chartype.CHAR_POINT
|
||||
elif ch == "+" or ch == "-":
|
||||
return Chartype.CHAR_SIGN
|
||||
else:
|
||||
return Chartype.CHAR_ILLEGAL
|
||||
|
||||
transfer = {
|
||||
State.STATE_INITIAL: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_INTEGER,
|
||||
Chartype.CHAR_POINT: State.STATE_POINT_WITHOUT_INT,
|
||||
Chartype.CHAR_SIGN: State.STATE_INT_SIGN
|
||||
},
|
||||
State.STATE_INT_SIGN: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_INTEGER,
|
||||
Chartype.CHAR_POINT: State.STATE_POINT_WITHOUT_INT
|
||||
},
|
||||
State.STATE_INTEGER: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_INTEGER,
|
||||
Chartype.CHAR_EXP: State.STATE_EXP,
|
||||
Chartype.CHAR_POINT: State.STATE_POINT
|
||||
},
|
||||
State.STATE_POINT: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_FRACTION,
|
||||
Chartype.CHAR_EXP: State.STATE_EXP
|
||||
},
|
||||
State.STATE_POINT_WITHOUT_INT: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_FRACTION
|
||||
},
|
||||
State.STATE_FRACTION: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_FRACTION,
|
||||
Chartype.CHAR_EXP: State.STATE_EXP
|
||||
},
|
||||
State.STATE_EXP: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_EXP_NUMBER,
|
||||
Chartype.CHAR_SIGN: State.STATE_EXP_SIGN
|
||||
},
|
||||
State.STATE_EXP_SIGN: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_EXP_NUMBER
|
||||
},
|
||||
State.STATE_EXP_NUMBER: {
|
||||
Chartype.CHAR_NUMBER: State.STATE_EXP_NUMBER
|
||||
},
|
||||
}
|
||||
|
||||
st = State.STATE_INITIAL
|
||||
for ch in s:
|
||||
typ = toChartype(ch)
|
||||
if typ not in transfer[st]:
|
||||
return False
|
||||
st = transfer[st][typ]
|
||||
|
||||
return st in [State.STATE_INTEGER, State.STATE_POINT, State.STATE_FRACTION, State.STATE_EXP_NUMBER, State.STATE_END]
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var isNumber = function(s) {
|
||||
const State = {
|
||||
STATE_INITIAL : "STATE_INITIAL",
|
||||
STATE_INT_SIGN : "STATE_INT_SIGN",
|
||||
STATE_INTEGER : "STATE_INTEGER",
|
||||
STATE_POINT : "STATE_POINT",
|
||||
STATE_POINT_WITHOUT_INT : "STATE_POINT_WITHOUT_INT",
|
||||
STATE_FRACTION : "STATE_FRACTION",
|
||||
STATE_EXP : "STATE_EXP",
|
||||
STATE_EXP_SIGN : "STATE_EXP_SIGN",
|
||||
STATE_EXP_NUMBER : "STATE_EXP_NUMBER",
|
||||
STATE_END : "STATE_END"
|
||||
}
|
||||
|
||||
const CharType = {
|
||||
CHAR_NUMBER : "CHAR_NUMBER",
|
||||
CHAR_EXP : "CHAR_EXP",
|
||||
CHAR_POINT : "CHAR_POINT",
|
||||
CHAR_SIGN : "CHAR_SIGN",
|
||||
CHAR_ILLEGAL : "CHAR_ILLEGAL"
|
||||
}
|
||||
|
||||
const toCharType = (ch) => {
|
||||
if (!isNaN(ch)) {
|
||||
return CharType.CHAR_NUMBER;
|
||||
} else if (ch.toLowerCase() === 'e') {
|
||||
return CharType.CHAR_EXP;
|
||||
} else if (ch === '.') {
|
||||
return CharType.CHAR_POINT;
|
||||
} else if (ch === '+' || ch === '-') {
|
||||
return CharType.CHAR_SIGN;
|
||||
} else {
|
||||
return CharType.CHAR_ILLEGAL;
|
||||
}
|
||||
}
|
||||
|
||||
const transfer = new Map();
|
||||
const initialMap = new Map();
|
||||
initialMap.set(CharType.CHAR_NUMBER, State.STATE_INTEGER);
|
||||
initialMap.set(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT);
|
||||
initialMap.set(CharType.CHAR_SIGN, State.STATE_INT_SIGN);
|
||||
transfer.set(State.STATE_INITIAL, initialMap);
|
||||
const intSignMap = new Map();
|
||||
intSignMap.set(CharType.CHAR_NUMBER, State.STATE_INTEGER);
|
||||
intSignMap.set(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT);
|
||||
transfer.set(State.STATE_INT_SIGN, intSignMap);
|
||||
const integerMap = new Map();
|
||||
integerMap.set(CharType.CHAR_NUMBER, State.STATE_INTEGER);
|
||||
integerMap.set(CharType.CHAR_EXP, State.STATE_EXP);
|
||||
integerMap.set(CharType.CHAR_POINT, State.STATE_POINT);
|
||||
transfer.set(State.STATE_INTEGER, integerMap);
|
||||
const pointMap = new Map()
|
||||
pointMap.set(CharType.CHAR_NUMBER, State.STATE_FRACTION);
|
||||
pointMap.set(CharType.CHAR_EXP, State.STATE_EXP);
|
||||
transfer.set(State.STATE_POINT, pointMap);
|
||||
const pointWithoutIntMap = new Map();
|
||||
pointWithoutIntMap.set(CharType.CHAR_NUMBER, State.STATE_FRACTION);
|
||||
transfer.set(State.STATE_POINT_WITHOUT_INT, pointWithoutIntMap);
|
||||
const fractionMap = new Map();
|
||||
fractionMap.set(CharType.CHAR_NUMBER, State.STATE_FRACTION);
|
||||
fractionMap.set(CharType.CHAR_EXP, State.STATE_EXP);
|
||||
transfer.set(State.STATE_FRACTION, fractionMap);
|
||||
const expMap = new Map();
|
||||
expMap.set(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
|
||||
expMap.set(CharType.CHAR_SIGN, State.STATE_EXP_SIGN);
|
||||
transfer.set(State.STATE_EXP, expMap);
|
||||
const expSignMap = new Map();
|
||||
expSignMap.set(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
|
||||
transfer.set(State.STATE_EXP_SIGN, expSignMap);
|
||||
const expNumberMap = new Map();
|
||||
expNumberMap.set(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
|
||||
transfer.set(State.STATE_EXP_NUMBER, expNumberMap);
|
||||
|
||||
const length = s.length;
|
||||
let state = State.STATE_INITIAL;
|
||||
|
||||
for (let i = 0; i < length; i++) {
|
||||
const type = toCharType(s[i]);
|
||||
if (!transfer.get(state).has(type)) {
|
||||
return false;
|
||||
} else {
|
||||
state = transfer.get(state).get(type);
|
||||
}
|
||||
}
|
||||
return state === State.STATE_INTEGER || state === State.STATE_POINT || state === State.STATE_FRACTION || state === State.STATE_EXP_NUMBER || state === State.STATE_END;
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n)$,其中 $n$ 为字符串的长度。我们需要遍历字符串的每个字符,其中状态转移所需的时间复杂度为 $O(1)$。
|
||||
|
||||
- 空间复杂度:$O(1)$。只需要创建固定大小的状态转移表。
|
||||
|
||||
@ -0,0 +1,577 @@
|
||||
#### 方法一:递归
|
||||
|
||||
由于非负整数 $\textit{num}$ 的最大值为 $2^{31}-1$,因此最多有 $10$ 位数。将整数转换成英文表示中,将数字按照 $3$ 位一组划分,将每一组的英文表示拼接之后即可得到整数 $\textit{num}$ 的英文表示。
|
||||
|
||||
每一组最多有 $3$ 位数,可以使用递归的方式得到每一组的英文表示。根据数字所在的范围,具体做法如下:
|
||||
|
||||
- 小于 $20$ 的数可以直接得到其英文表示;
|
||||
|
||||
- 大于等于 $20$ 且小于 $100$ 的数首先将十位转换成英文表示,然后对个位递归地转换成英文表示;
|
||||
|
||||
- 大于等于 $100$ 的数首先将百位转换成英文表示,然后对其余部分(十位和个位)递归地转换成英文表示。
|
||||
|
||||
从高到低的每一组的单位依次是 $10^9$、$10^6$、$10^3$、$1$,除了最低组以外,每一组都有对应的表示单位的词,分别是 $\text{``Billion"}$、$\text{``Million"}$、$\text{``Thousand"}$。
|
||||
|
||||
得到每一组的英文表示后,需要对每一组加上对应的表示单位的词,然后拼接得到整数 $\textit{num}$ 的英文表示。
|
||||
|
||||
具体实现中需要注意以下两点:
|
||||
|
||||
- 只有非零的组的英文表示才会拼接到整数 $\textit{num}$ 的英文表示中;
|
||||
|
||||
- 如果 $\textit{num} = 0$,则不适用上述做法,而是直接返回 $\text{``Zero"}$。
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
String[] singles = {"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"};
|
||||
String[] teens = {"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
|
||||
String[] tens = {"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
|
||||
String[] thousands = {"", "Thousand", "Million", "Billion"};
|
||||
|
||||
public String numberToWords(int num) {
|
||||
if (num == 0) {
|
||||
return "Zero";
|
||||
}
|
||||
StringBuffer sb = new StringBuffer();
|
||||
for (int i = 3, unit = 1000000000; i >= 0; i--, unit /= 1000) {
|
||||
int curNum = num / unit;
|
||||
if (curNum != 0) {
|
||||
num -= curNum * unit;
|
||||
StringBuffer curr = new StringBuffer();
|
||||
recursion(curr, curNum);
|
||||
curr.append(thousands[i]).append(" ");
|
||||
sb.append(curr);
|
||||
}
|
||||
}
|
||||
return sb.toString().trim();
|
||||
}
|
||||
|
||||
public void recursion(StringBuffer curr, int num) {
|
||||
if (num == 0) {
|
||||
return;
|
||||
} else if (num < 10) {
|
||||
curr.append(singles[num]).append(" ");
|
||||
} else if (num < 20) {
|
||||
curr.append(teens[num - 10]).append(" ");
|
||||
} else if (num < 100) {
|
||||
curr.append(tens[num / 10]).append(" ");
|
||||
recursion(curr, num % 10);
|
||||
} else {
|
||||
curr.append(singles[num / 100]).append(" Hundred ");
|
||||
recursion(curr, num % 100);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
string[] singles = {"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"};
|
||||
string[] teens = {"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
|
||||
string[] tens = {"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
|
||||
string[] thousands = {"", "Thousand", "Million", "Billion"};
|
||||
|
||||
public string NumberToWords(int num) {
|
||||
if (num == 0) {
|
||||
return "Zero";
|
||||
}
|
||||
StringBuilder sb = new StringBuilder();
|
||||
for (int i = 3, unit = 1000000000; i >= 0; i--, unit /= 1000) {
|
||||
int curNum = num / unit;
|
||||
if (curNum != 0) {
|
||||
num -= curNum * unit;
|
||||
StringBuilder curr = new StringBuilder();
|
||||
Recursion(curr, curNum);
|
||||
curr.Append(thousands[i]).Append(" ");
|
||||
sb.Append(curr);
|
||||
}
|
||||
}
|
||||
return sb.ToString().Trim();
|
||||
}
|
||||
|
||||
public void Recursion(StringBuilder curr, int num) {
|
||||
if (num == 0) {
|
||||
return;
|
||||
} else if (num < 10) {
|
||||
curr.Append(singles[num]).Append(" ");
|
||||
} else if (num < 20) {
|
||||
curr.Append(teens[num - 10]).Append(" ");
|
||||
} else if (num < 100) {
|
||||
curr.Append(tens[num / 10]).Append(" ");
|
||||
Recursion(curr, num % 10);
|
||||
} else {
|
||||
curr.Append(singles[num / 100]).Append(" Hundred ");
|
||||
Recursion(curr, num % 100);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
vector<string> singles = {"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"};
|
||||
vector<string> teens = {"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
|
||||
vector<string> tens = {"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
|
||||
vector<string> thousands = {"", "Thousand", "Million", "Billion"};
|
||||
|
||||
string numberToWords(int num) {
|
||||
if (num == 0) {
|
||||
return "Zero";
|
||||
}
|
||||
string sb;
|
||||
for (int i = 3, unit = 1000000000; i >= 0; i--, unit /= 1000) {
|
||||
int curNum = num / unit;
|
||||
if (curNum != 0) {
|
||||
num -= curNum * unit;
|
||||
string curr;
|
||||
recursion(curr, curNum);
|
||||
curr = curr + thousands[i] + " ";
|
||||
sb = sb + curr;
|
||||
}
|
||||
}
|
||||
while (sb.back() == ' ') {
|
||||
sb.pop_back();
|
||||
}
|
||||
return sb;
|
||||
}
|
||||
|
||||
void recursion(string & curr, int num) {
|
||||
if (num == 0) {
|
||||
return;
|
||||
} else if (num < 10) {
|
||||
curr = curr + singles[num] + " ";
|
||||
} else if (num < 20) {
|
||||
curr = curr + teens[num - 10] + " ";
|
||||
} else if (num < 100) {
|
||||
curr = curr + tens[num / 10] + " ";
|
||||
recursion(curr, num % 10);
|
||||
} else {
|
||||
curr = curr + singles[num / 100] + " Hundred ";
|
||||
recursion(curr, num % 100);
|
||||
}
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var numberToWords = function(num) {
|
||||
const singles = ["", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"];
|
||||
const teens = ["Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"];
|
||||
const tens = ["", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"];
|
||||
const thousands = ["", "Thousand", "Million", "Billion"];
|
||||
|
||||
const recursion = (curr, num) => {
|
||||
if (num === 0) {
|
||||
return;
|
||||
} else if (num < 10) {
|
||||
curr.push(singles[num] + " ");
|
||||
} else if (num < 20) {
|
||||
curr.push(teens[num - 10] + " ");
|
||||
} else if (num < 100) {
|
||||
curr.push(tens[Math.floor(num / 10)] + " ");
|
||||
recursion(curr, num % 10);
|
||||
} else {
|
||||
curr.push(singles[Math.floor(num / 100)] + " Hundred ");
|
||||
recursion(curr, num % 100);
|
||||
}
|
||||
}
|
||||
|
||||
if (num === 0) {
|
||||
return "Zero";
|
||||
}
|
||||
const sb = [];
|
||||
for (let i = 3, unit = 1000000000; i >= 0; i--, unit = Math.floor(unit / 1000)) {
|
||||
const curNum = Math.floor(num / unit);
|
||||
if (curNum !== 0) {
|
||||
num -= curNum * unit;
|
||||
const curr = [];
|
||||
recursion(curr, curNum);
|
||||
curr.push(thousands[i] + " ");
|
||||
sb.push(curr.join(''));
|
||||
}
|
||||
}
|
||||
return sb.join('').trim();
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
var (
|
||||
singles = []string{"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"}
|
||||
teens = []string{"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"}
|
||||
tens = []string{"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"}
|
||||
thousands = []string{"", "Thousand", "Million", "Billion"}
|
||||
)
|
||||
|
||||
func numberToWords(num int) string {
|
||||
if num == 0 {
|
||||
return "Zero"
|
||||
}
|
||||
sb := &strings.Builder{}
|
||||
var recursion func(int)
|
||||
recursion = func(num int) {
|
||||
switch {
|
||||
case num == 0:
|
||||
case num < 10:
|
||||
sb.WriteString(singles[num])
|
||||
sb.WriteByte(' ')
|
||||
case num < 20:
|
||||
sb.WriteString(teens[num-10])
|
||||
sb.WriteByte(' ')
|
||||
case num < 100:
|
||||
sb.WriteString(tens[num/10])
|
||||
sb.WriteByte(' ')
|
||||
recursion(num % 10)
|
||||
default:
|
||||
sb.WriteString(singles[num/100])
|
||||
sb.WriteString(" Hundred ")
|
||||
recursion(num % 100)
|
||||
}
|
||||
}
|
||||
for i, unit := 3, int(1e9); i >= 0; i-- {
|
||||
if curNum := num / unit; curNum > 0 {
|
||||
num -= curNum * unit
|
||||
recursion(curNum)
|
||||
sb.WriteString(thousands[i])
|
||||
sb.WriteByte(' ')
|
||||
}
|
||||
unit /= 1000
|
||||
}
|
||||
return strings.TrimSpace(sb.String())
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
singles = ["", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"]
|
||||
teens = ["Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"]
|
||||
tens = ["", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"]
|
||||
thousands = ["", "Thousand", "Million", "Billion"]
|
||||
|
||||
class Solution:
|
||||
def numberToWords(self, num: int) -> str:
|
||||
if num == 0:
|
||||
return "Zero"
|
||||
|
||||
def recursion(num: int) -> str:
|
||||
s = ""
|
||||
if num == 0:
|
||||
return s
|
||||
elif num < 10:
|
||||
s += singles[num] + " "
|
||||
elif num < 20:
|
||||
s += teens[num - 10] + " "
|
||||
elif num < 100:
|
||||
s += tens[num // 10] + " " + recursion(num % 10)
|
||||
else:
|
||||
s += singles[num // 100] + " Hundred " + recursion(num % 100)
|
||||
return s
|
||||
|
||||
s = ""
|
||||
unit = int(1e9)
|
||||
for i in range(3, -1, -1):
|
||||
curNum = num // unit
|
||||
if curNum:
|
||||
num -= curNum * unit
|
||||
s += recursion(curNum) + thousands[i] + " "
|
||||
unit //= 1000
|
||||
return s.strip()
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(1)$。非负整数 $\textit{nums}$ 按照 $3$ 位一组划分最多有 $4$ 组,分别得到每一组的英文表示,然后拼接得到整数 $\textit{num}$ 的英文表示,时间复杂度是常数。
|
||||
|
||||
- 空间复杂度:$O(1)$。空间复杂度主要取决于存储英文表示的字符串和递归调用栈,英文表示的长度可以看成常数,递归调用栈不会超过 $3$ 层。
|
||||
|
||||
#### 方法二:迭代
|
||||
|
||||
也可以使用迭代的方式得到每一组的英文表示。由于每一组最多有 $3$ 位数,因此依次得到百位、十位、个位上的数字,生成该组的英文表示,注意只有非零位才会被添加到英文表示中。
|
||||
|
||||
* [sol2-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
String[] singles = {"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"};
|
||||
String[] teens = {"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
|
||||
String[] tens = {"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
|
||||
String[] thousands = {"", "Thousand", "Million", "Billion"};
|
||||
|
||||
public String numberToWords(int num) {
|
||||
if (num == 0) {
|
||||
return "Zero";
|
||||
}
|
||||
StringBuffer sb = new StringBuffer();
|
||||
for (int i = 3, unit = 1000000000; i >= 0; i--, unit /= 1000) {
|
||||
int curNum = num / unit;
|
||||
if (curNum != 0) {
|
||||
num -= curNum * unit;
|
||||
sb.append(toEnglish(curNum)).append(thousands[i]).append(" ");
|
||||
}
|
||||
}
|
||||
return sb.toString().trim();
|
||||
}
|
||||
|
||||
public String toEnglish(int num) {
|
||||
StringBuffer curr = new StringBuffer();
|
||||
int hundred = num / 100;
|
||||
num %= 100;
|
||||
if (hundred != 0) {
|
||||
curr.append(singles[hundred]).append(" Hundred ");
|
||||
}
|
||||
int ten = num / 10;
|
||||
if (ten >= 2) {
|
||||
curr.append(tens[ten]).append(" ");
|
||||
num %= 10;
|
||||
}
|
||||
if (num > 0 && num < 10) {
|
||||
curr.append(singles[num]).append(" ");
|
||||
} else if (num >= 10) {
|
||||
curr.append(teens[num - 10]).append(" ");
|
||||
}
|
||||
return curr.toString();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
string[] singles = {"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"};
|
||||
string[] teens = {"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
|
||||
string[] tens = {"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
|
||||
string[] thousands = {"", "Thousand", "Million", "Billion"};
|
||||
|
||||
public string NumberToWords(int num) {
|
||||
if (num == 0) {
|
||||
return "Zero";
|
||||
}
|
||||
StringBuilder sb = new StringBuilder();
|
||||
for (int i = 3, unit = 1000000000; i >= 0; i--, unit /= 1000) {
|
||||
int curNum = num / unit;
|
||||
if (curNum != 0) {
|
||||
num -= curNum * unit;
|
||||
sb.Append(toEnglish(curNum)).Append(thousands[i]).Append(" ");
|
||||
}
|
||||
}
|
||||
return sb.ToString().Trim();
|
||||
}
|
||||
|
||||
public string toEnglish(int num) {
|
||||
StringBuilder curr = new StringBuilder();
|
||||
int hundred = num / 100;
|
||||
num %= 100;
|
||||
if (hundred != 0) {
|
||||
curr.Append(singles[hundred]).Append(" Hundred ");
|
||||
}
|
||||
int ten = num / 10;
|
||||
if (ten >= 2) {
|
||||
curr.Append(tens[ten]).Append(" ");
|
||||
num %= 10;
|
||||
}
|
||||
if (num > 0 && num < 10) {
|
||||
curr.Append(singles[num]).Append(" ");
|
||||
} else if (num >= 10) {
|
||||
curr.Append(teens[num - 10]).Append(" ");
|
||||
}
|
||||
return curr.ToString();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
vector<string> singles = {"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"};
|
||||
vector<string> teens = {"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"};
|
||||
vector<string> tens = {"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"};
|
||||
vector<string> thousands = {"", "Thousand", "Million", "Billion"};
|
||||
|
||||
string numberToWords(int num) {
|
||||
if (num == 0) {
|
||||
return "Zero";
|
||||
}
|
||||
string sb;
|
||||
for (int i = 3, unit = 1000000000; i >= 0; i--, unit /= 1000) {
|
||||
int curNum = num / unit;
|
||||
if (curNum != 0) {
|
||||
num -= curNum * unit;
|
||||
sb = sb + toEnglish(curNum) + thousands[i] + " ";
|
||||
}
|
||||
}
|
||||
while (sb.back() == ' ') {
|
||||
sb.pop_back();
|
||||
}
|
||||
return sb;
|
||||
}
|
||||
|
||||
string toEnglish(int num) {
|
||||
string curr;
|
||||
int hundred = num / 100;
|
||||
num %= 100;
|
||||
if (hundred != 0) {
|
||||
curr = curr + singles[hundred] + " Hundred ";
|
||||
}
|
||||
int ten = num / 10;
|
||||
if (ten >= 2) {
|
||||
curr = curr + tens[ten] + " ";
|
||||
num %= 10;
|
||||
}
|
||||
if (num > 0 && num < 10) {
|
||||
curr = curr + singles[num] + " ";
|
||||
} else if (num >= 10) {
|
||||
curr = curr + teens[num - 10] + " ";
|
||||
}
|
||||
return curr;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var numberToWords = function(num) {
|
||||
const singles = ["", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"];
|
||||
const teens = ["Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"];
|
||||
const tens = ["", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"];
|
||||
const thousands = ["", "Thousand", "Million", "Billion"];
|
||||
|
||||
const toEnglish = (num) => {
|
||||
const curr = [];
|
||||
const hundred = Math.floor(num / 100);
|
||||
num %= 100;
|
||||
if (hundred !== 0) {
|
||||
curr.push(singles[hundred] + " Hundred ");
|
||||
}
|
||||
const ten = Math.floor(num / 10);
|
||||
if (ten >= 2) {
|
||||
curr.push(tens[ten] + " ");
|
||||
num %= 10;
|
||||
}
|
||||
if (num > 0 && num < 10) {
|
||||
curr.push(singles[num] + " ");
|
||||
} else if (num >= 10) {
|
||||
curr.push(teens[num - 10] + " ");
|
||||
}
|
||||
return curr.join('');
|
||||
}
|
||||
|
||||
if (num === 0) {
|
||||
return "Zero";
|
||||
}
|
||||
const sb = [];
|
||||
for (let i = 3, unit = 1000000000; i >= 0; i--, unit = Math.floor(unit / 1000)) {
|
||||
const curNum = Math.floor(num / unit);
|
||||
if (curNum !== 0) {
|
||||
num -= curNum * unit;
|
||||
sb.push(toEnglish(curNum) + thousands[i] + " ");
|
||||
}
|
||||
}
|
||||
return sb.join('').trim();
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Golang]
|
||||
|
||||
```go
|
||||
var (
|
||||
singles = []string{"", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"}
|
||||
teens = []string{"Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"}
|
||||
tens = []string{"", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"}
|
||||
thousands = []string{"", "Thousand", "Million", "Billion"}
|
||||
)
|
||||
|
||||
func numberToWords(num int) string {
|
||||
if num == 0 {
|
||||
return "Zero"
|
||||
}
|
||||
sb := &strings.Builder{}
|
||||
toEnglish := func(num int) {
|
||||
if num >= 100 {
|
||||
sb.WriteString(singles[num/100])
|
||||
sb.WriteString(" Hundred ")
|
||||
num %= 100
|
||||
}
|
||||
if num >= 20 {
|
||||
sb.WriteString(tens[num/10])
|
||||
sb.WriteByte(' ')
|
||||
num %= 10
|
||||
}
|
||||
if 0 < num && num < 10 {
|
||||
sb.WriteString(singles[num])
|
||||
sb.WriteByte(' ')
|
||||
} else if num >= 10 {
|
||||
sb.WriteString(teens[num-10])
|
||||
sb.WriteByte(' ')
|
||||
}
|
||||
}
|
||||
for i, unit := 3, int(1e9); i >= 0; i-- {
|
||||
if curNum := num / unit; curNum > 0 {
|
||||
num -= curNum * unit
|
||||
toEnglish(curNum)
|
||||
sb.WriteString(thousands[i])
|
||||
sb.WriteByte(' ')
|
||||
}
|
||||
unit /= 1000
|
||||
}
|
||||
return strings.TrimSpace(sb.String())
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Python3]
|
||||
|
||||
```Python
|
||||
singles = ["", "One", "Two", "Three", "Four", "Five", "Six", "Seven", "Eight", "Nine"]
|
||||
teens = ["Ten", "Eleven", "Twelve", "Thirteen", "Fourteen", "Fifteen", "Sixteen", "Seventeen", "Eighteen", "Nineteen"]
|
||||
tens = ["", "Ten", "Twenty", "Thirty", "Forty", "Fifty", "Sixty", "Seventy", "Eighty", "Ninety"]
|
||||
thousands = ["", "Thousand", "Million", "Billion"]
|
||||
|
||||
class Solution:
|
||||
def numberToWords(self, num: int) -> str:
|
||||
if num == 0:
|
||||
return "Zero"
|
||||
|
||||
def toEnglish(num: int) -> str:
|
||||
s = ""
|
||||
if num >= 100:
|
||||
s += singles[num // 100] + " Hundred "
|
||||
num %= 100
|
||||
if num >= 20:
|
||||
s += tens[num // 10] + " "
|
||||
num %= 10
|
||||
if 0 < num < 10:
|
||||
s += singles[num] + " "
|
||||
elif num >= 10:
|
||||
s += teens[num - 10] + " "
|
||||
return s
|
||||
|
||||
s = ""
|
||||
unit = int(1e9)
|
||||
for i in range(3, -1, -1):
|
||||
curNum = num // unit
|
||||
if curNum:
|
||||
num -= curNum * unit
|
||||
s += toEnglish(curNum) + thousands[i] + " "
|
||||
unit //= 1000
|
||||
return s.strip()
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(1)$。
|
||||
|
||||
- 空间复杂度:$O(1)$。
|
||||
|
||||
@ -0,0 +1,117 @@
|
||||
#### 方法 1:滑动窗口
|
||||
|
||||
**想法**
|
||||
|
||||
为了遍历一遍就得到答案,我们使用一个左指针和一个右指针表示滑动窗口的边界。
|
||||
|
||||
一开始,让两个指针都指向 0 ,当窗口包含的字符不超过 2 个不同的字符时,就不断将右指针往右边移动。如果在某一个位置有 3 个不同的字符,就开始移动左指针,直到窗口内包含不超过 2 个不同字符。
|
||||
|
||||
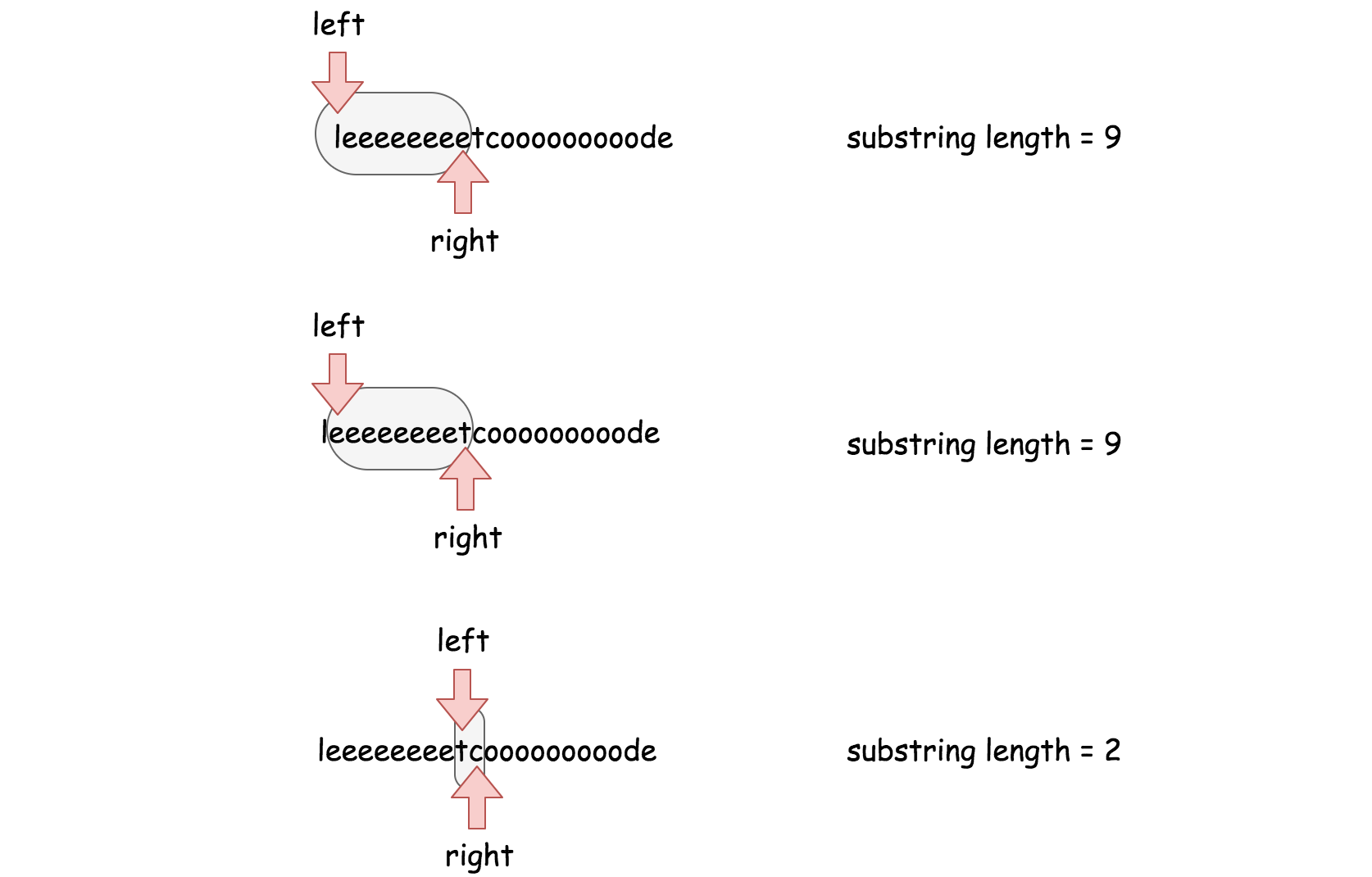
|
||||
|
||||
这就是基本的想法:沿着字符串移动滑动窗口,并保持窗口内只有不超过 2 个不同字符,同时每一步都更新最长子串的长度。
|
||||
|
||||
只有一个问题还没解决 - 如何移动左指针确保窗口内只有 2 种不同的字符?
|
||||
|
||||
我们使用一个 hashmap ,把字符串里的字符都当做键,在窗口中的最右边的字符位置作为值。每一个时刻,这个 hashmap 包括不超过 3 个元素。
|
||||
|
||||
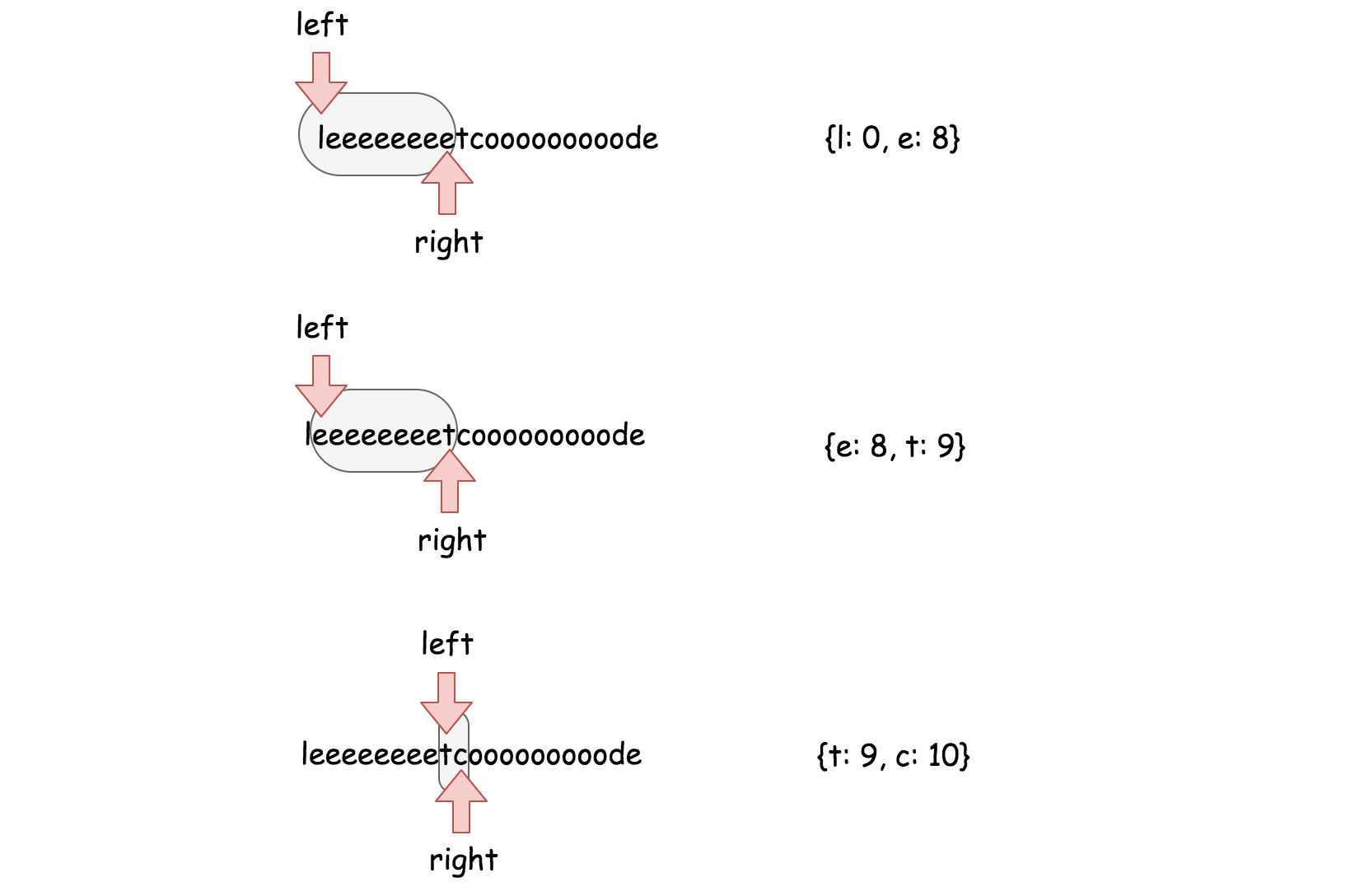
|
||||
|
||||
比方说,通过这个 hashmap ,你可以知道窗口 "eeeeeeeet" 中字符 e 最右边的位置是 8 ,所以必须要至少将左指针移动到 8 + 1 = 9 的位置来将 e 从滑动窗口中移除。
|
||||
|
||||
我们的方法时间复杂度是否是最优的呢?答案是是的。我们只将字符串的 N 个字符遍历了一次,时间复杂度是 $\mathcal{O}(N)$ 。
|
||||
|
||||
**算法**
|
||||
|
||||
现在我们可以写出如下算法:
|
||||
|
||||
- 如果 `N` 的长度小于 `3` ,返回 `N` 。
|
||||
- 将左右指针都初始化成字符串的左端点 `left = 0` 和 `right = 0` ,且初始化最大子字符串为 `max_len = 2`
|
||||
- 当右指针小于 `N` 时:
|
||||
* 如果 hashmap 包含小于 `3` 个不同字符,那么将当前字符 `s[right]` 放到 hashmap 中并将右指针往右移动一次。
|
||||
* 如果 hashmap 包含 `3` 个不同字符,将最左边的字符从 哈希表中删去,并移动左指针,以便滑动窗口只包含 `2` 个不同的字符。
|
||||
* 更新 `max_len`
|
||||
|
||||
**算法实现**
|
||||
|
||||
<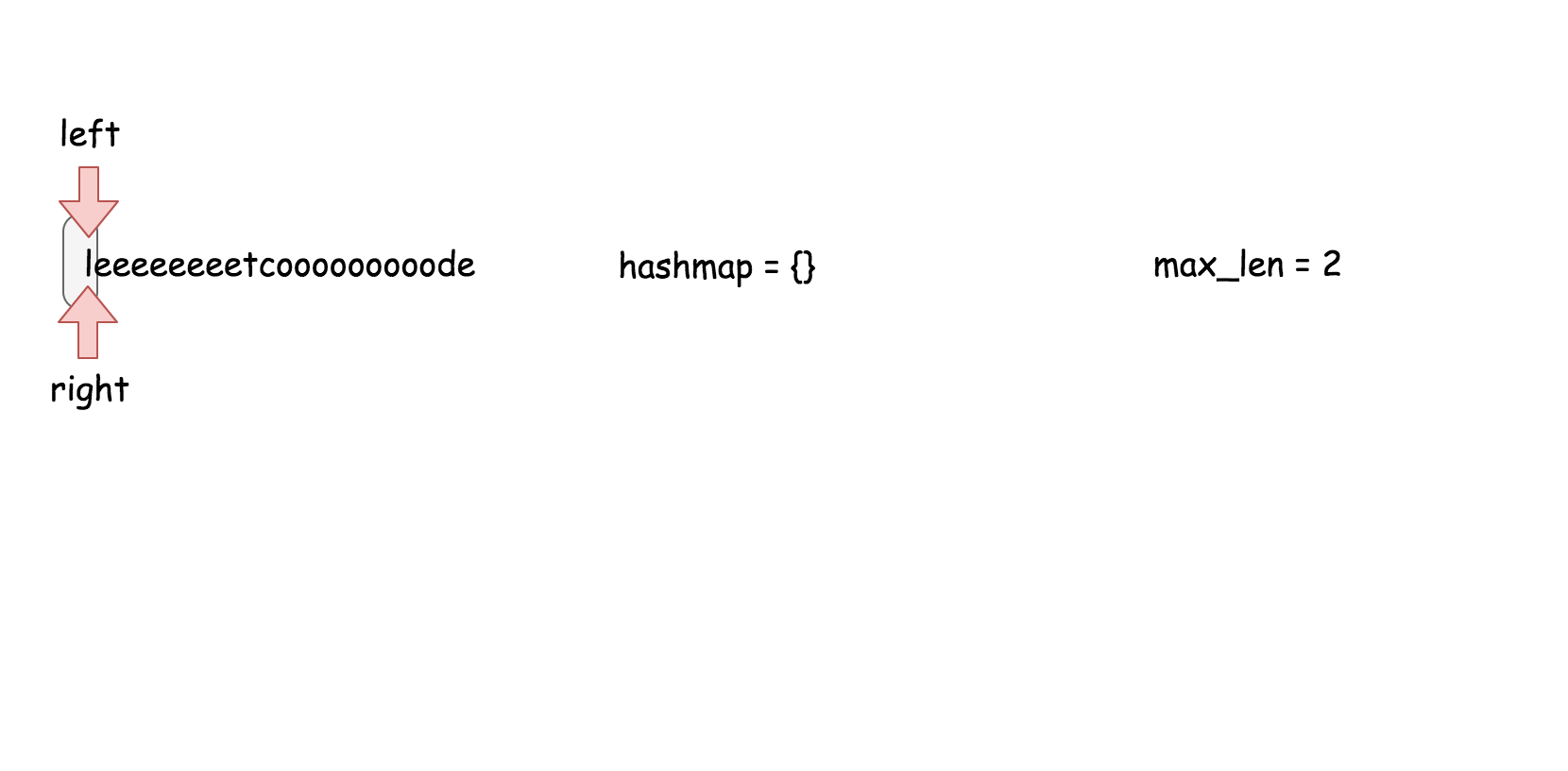,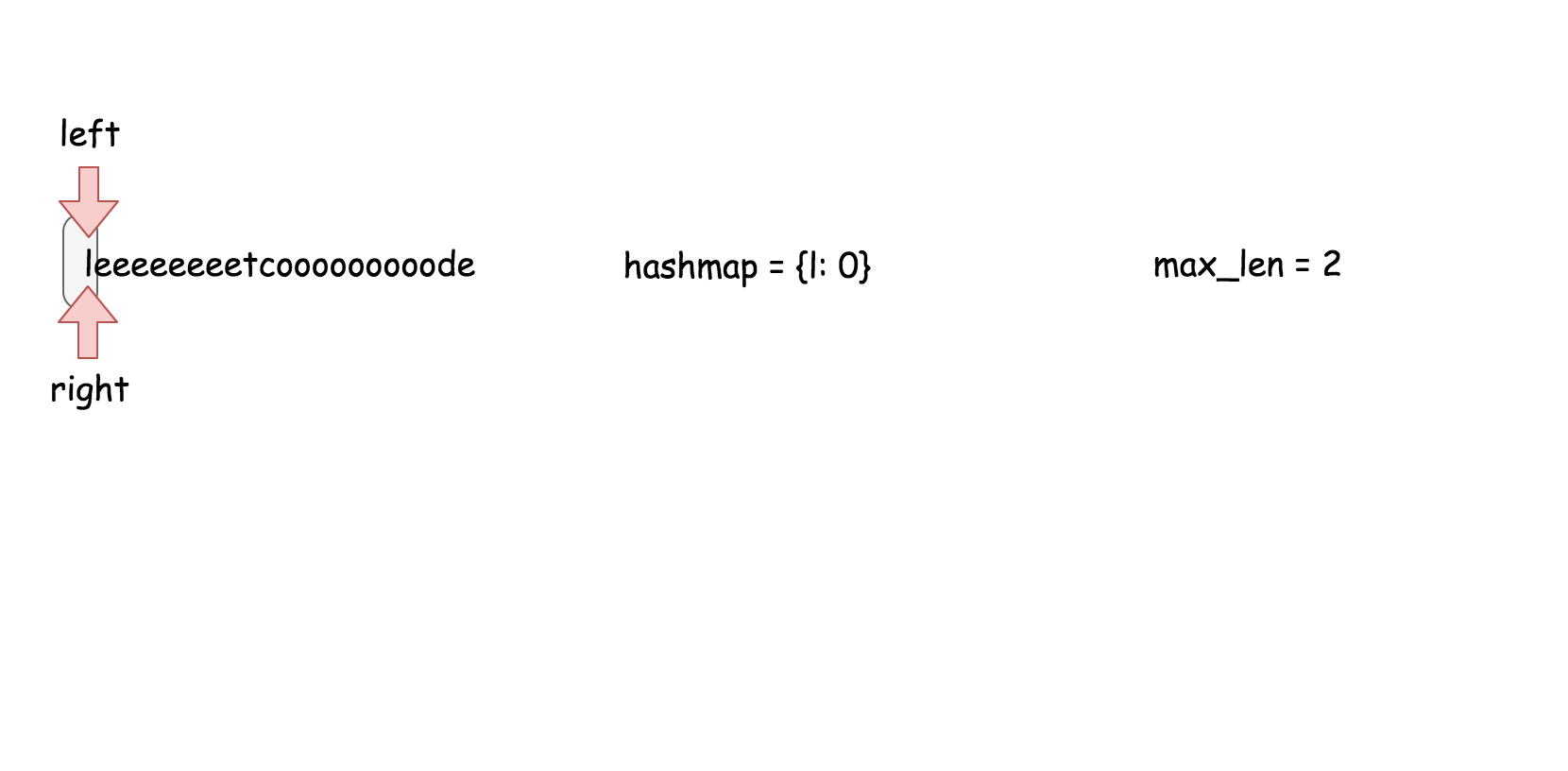,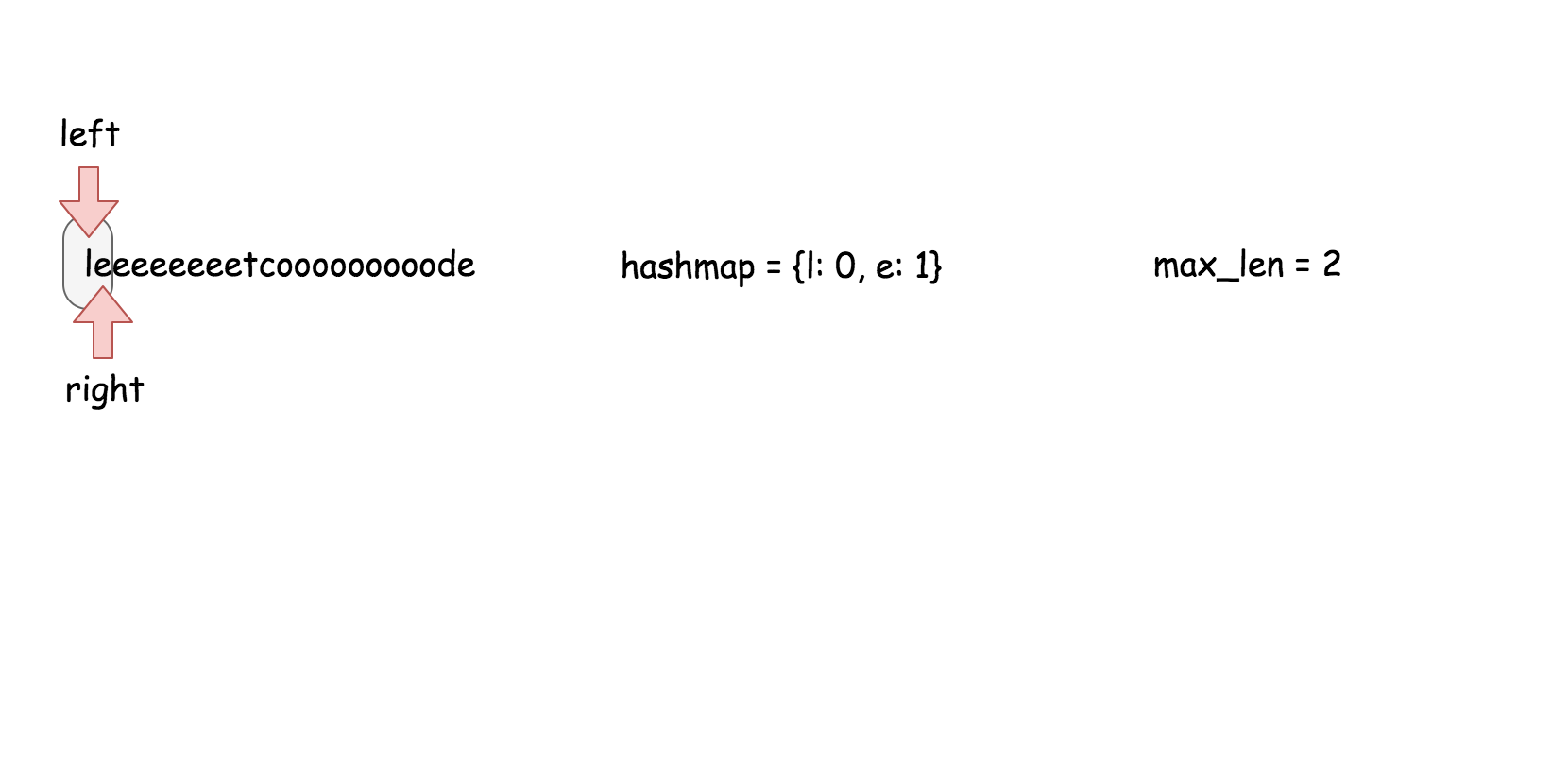,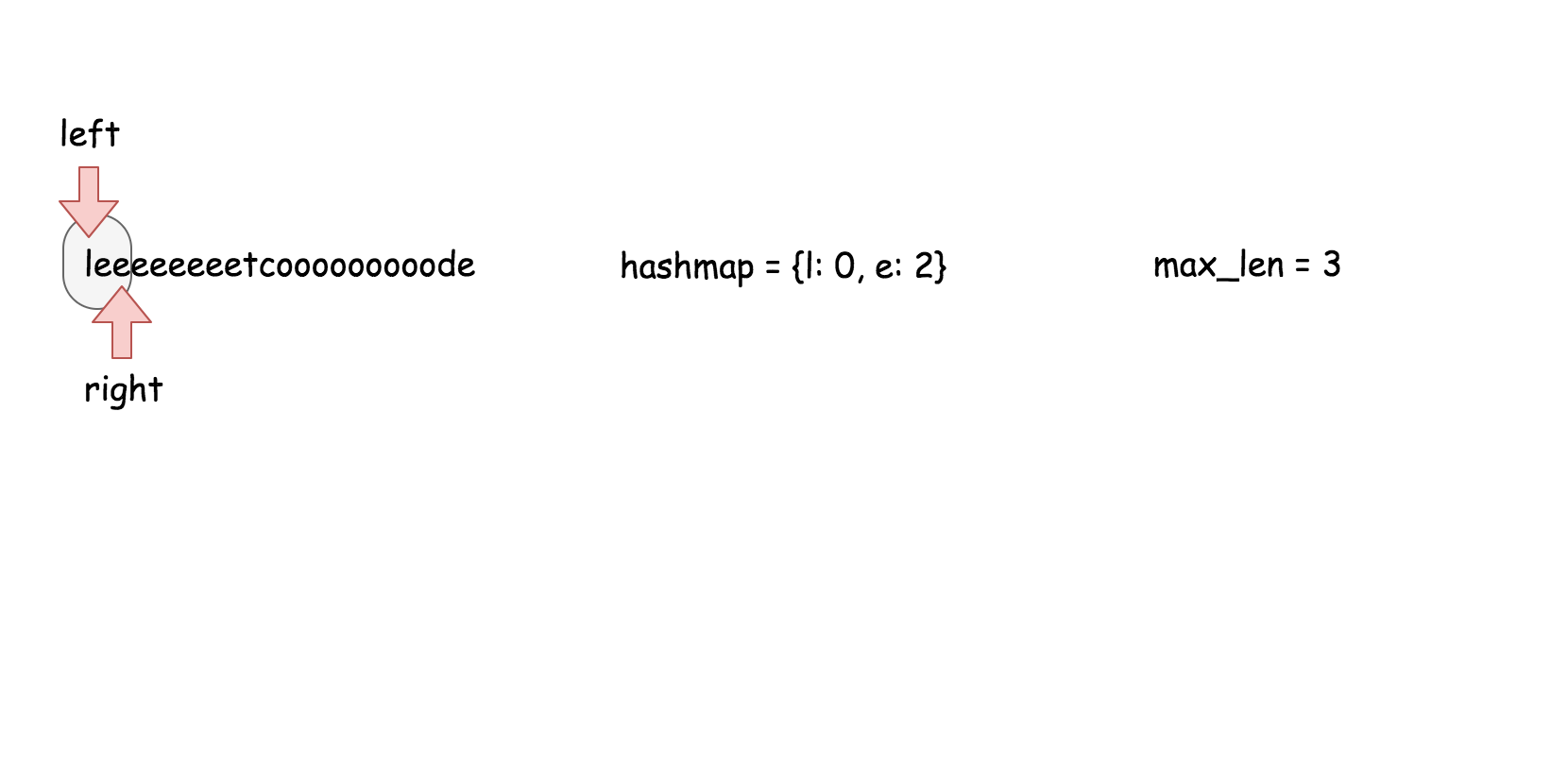,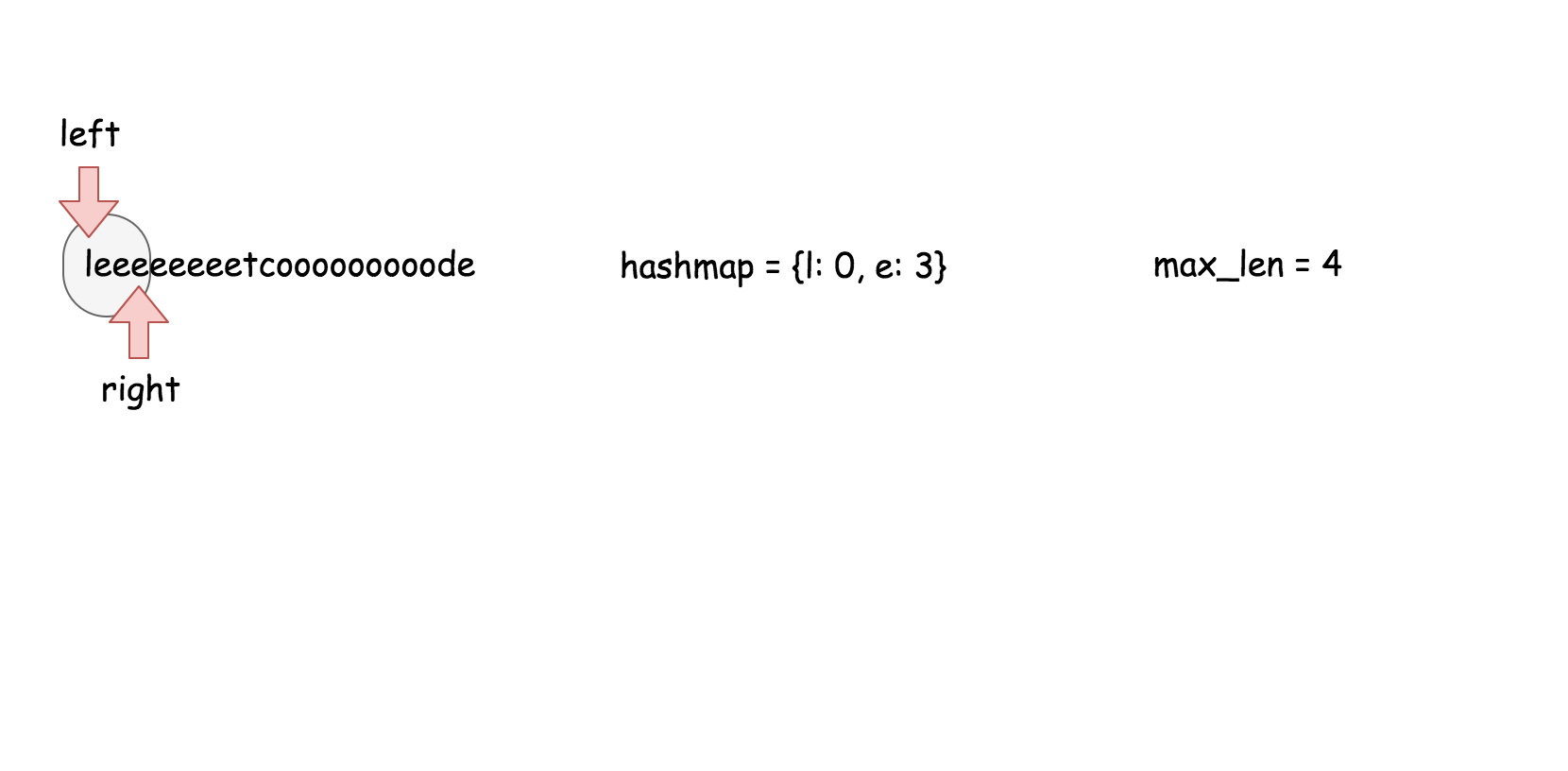,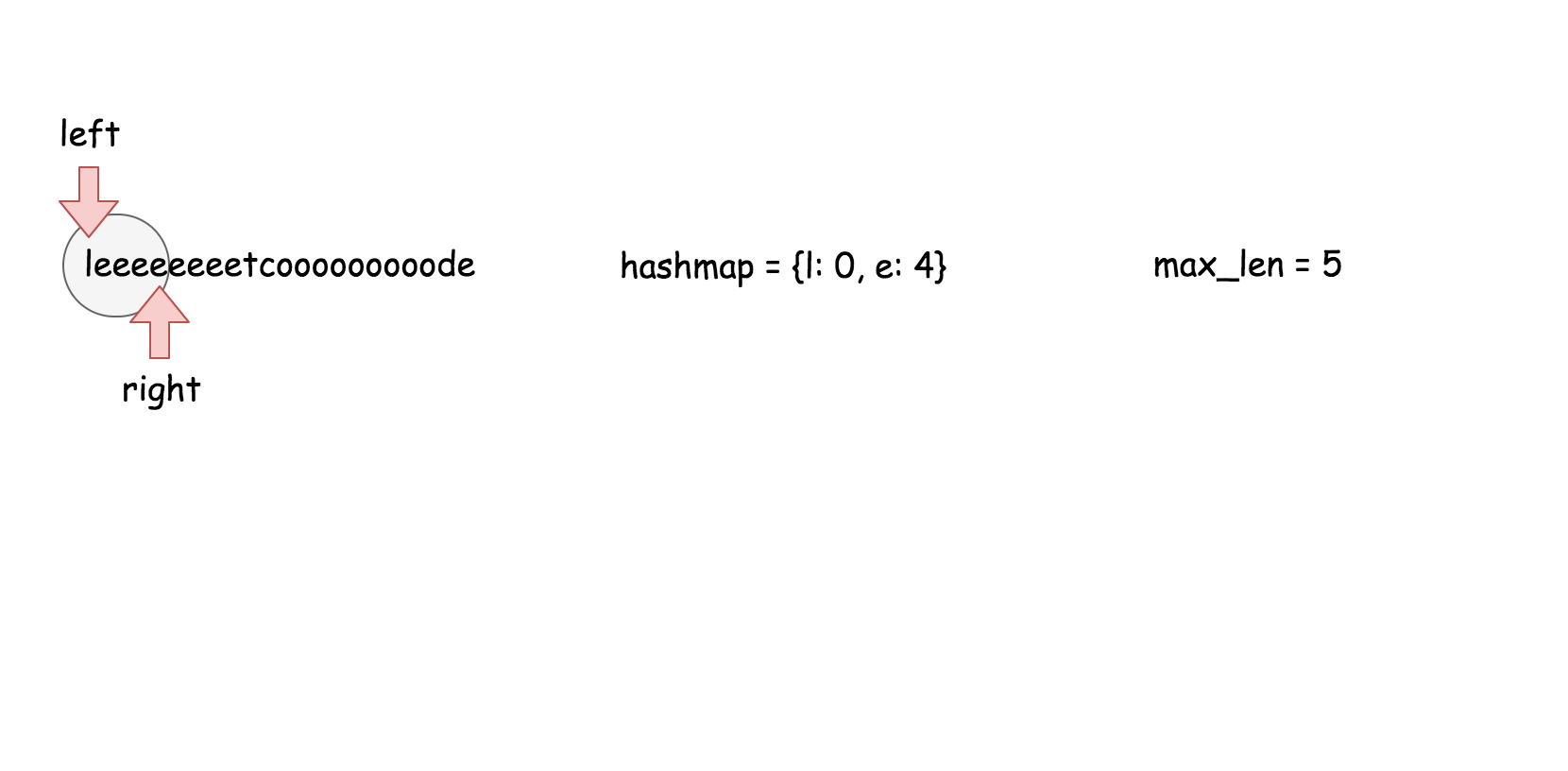,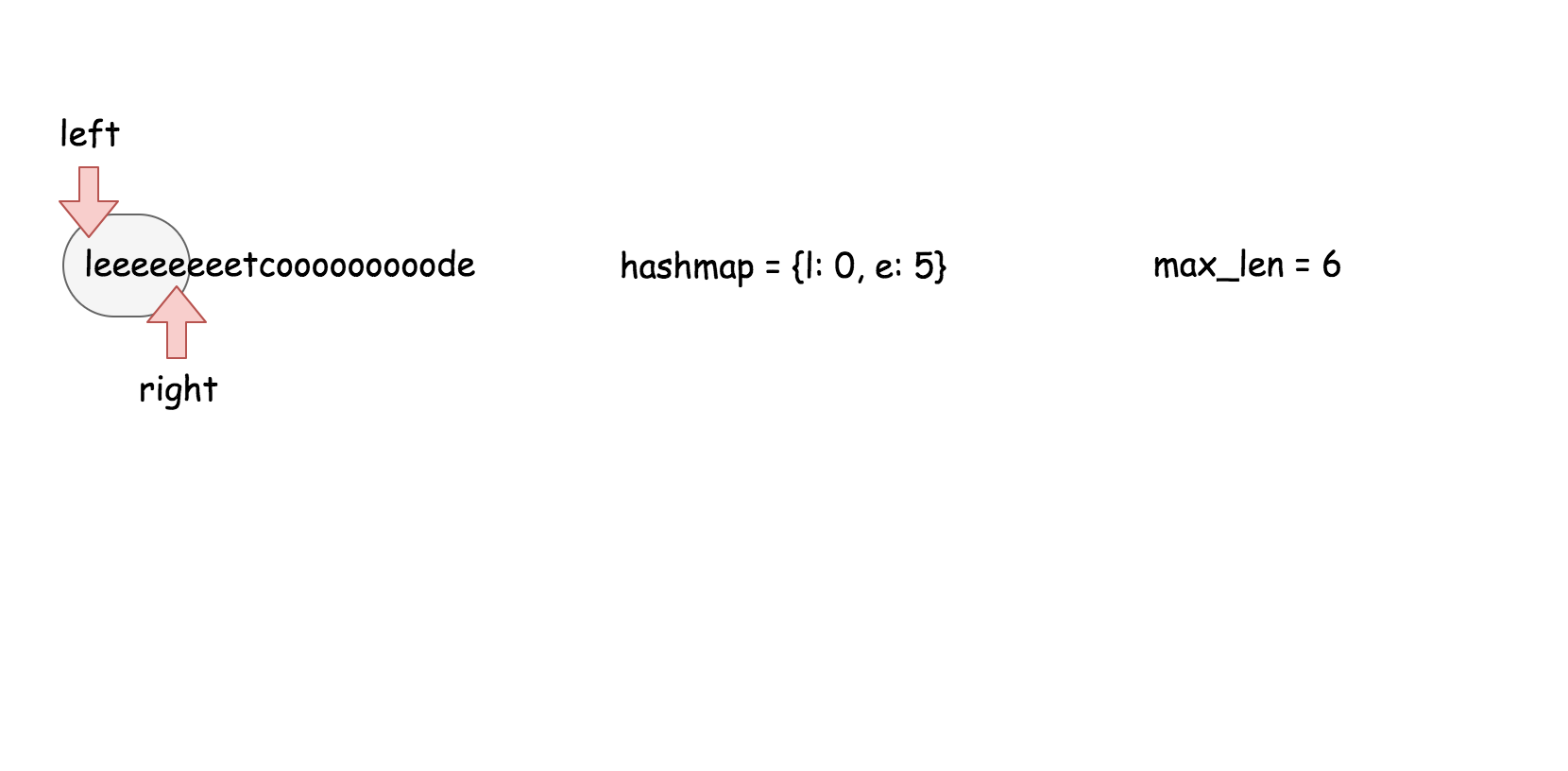,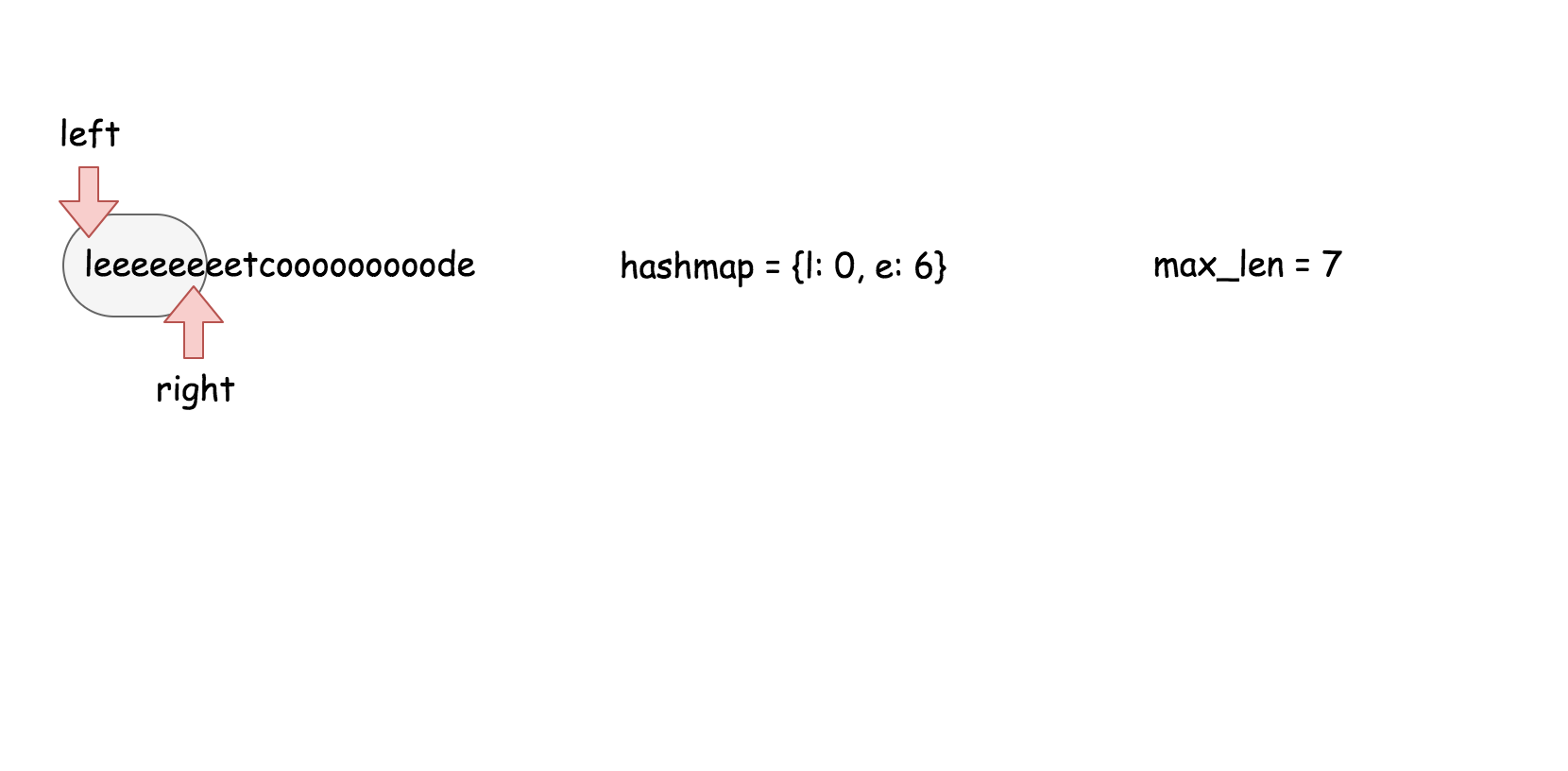,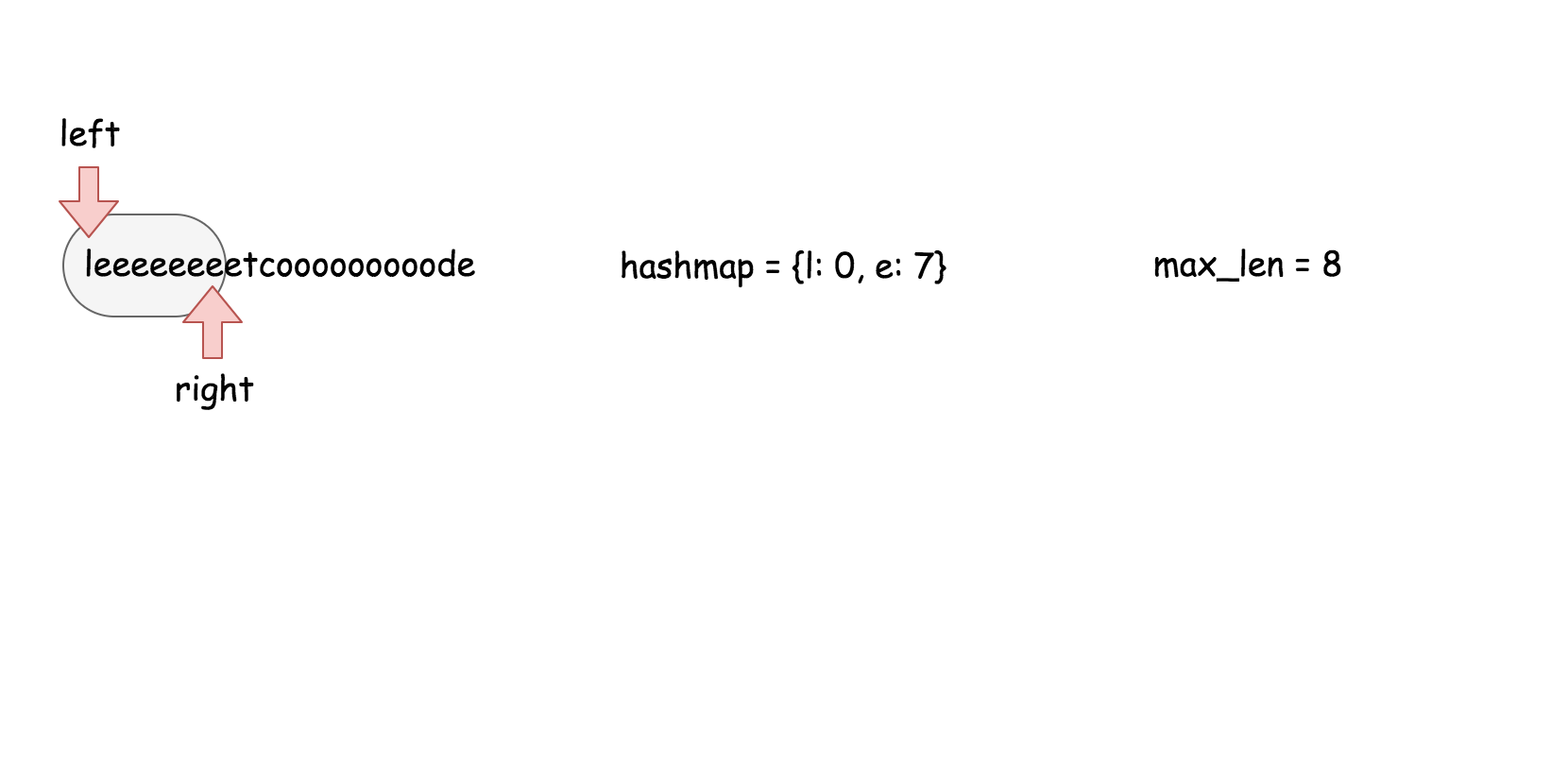, 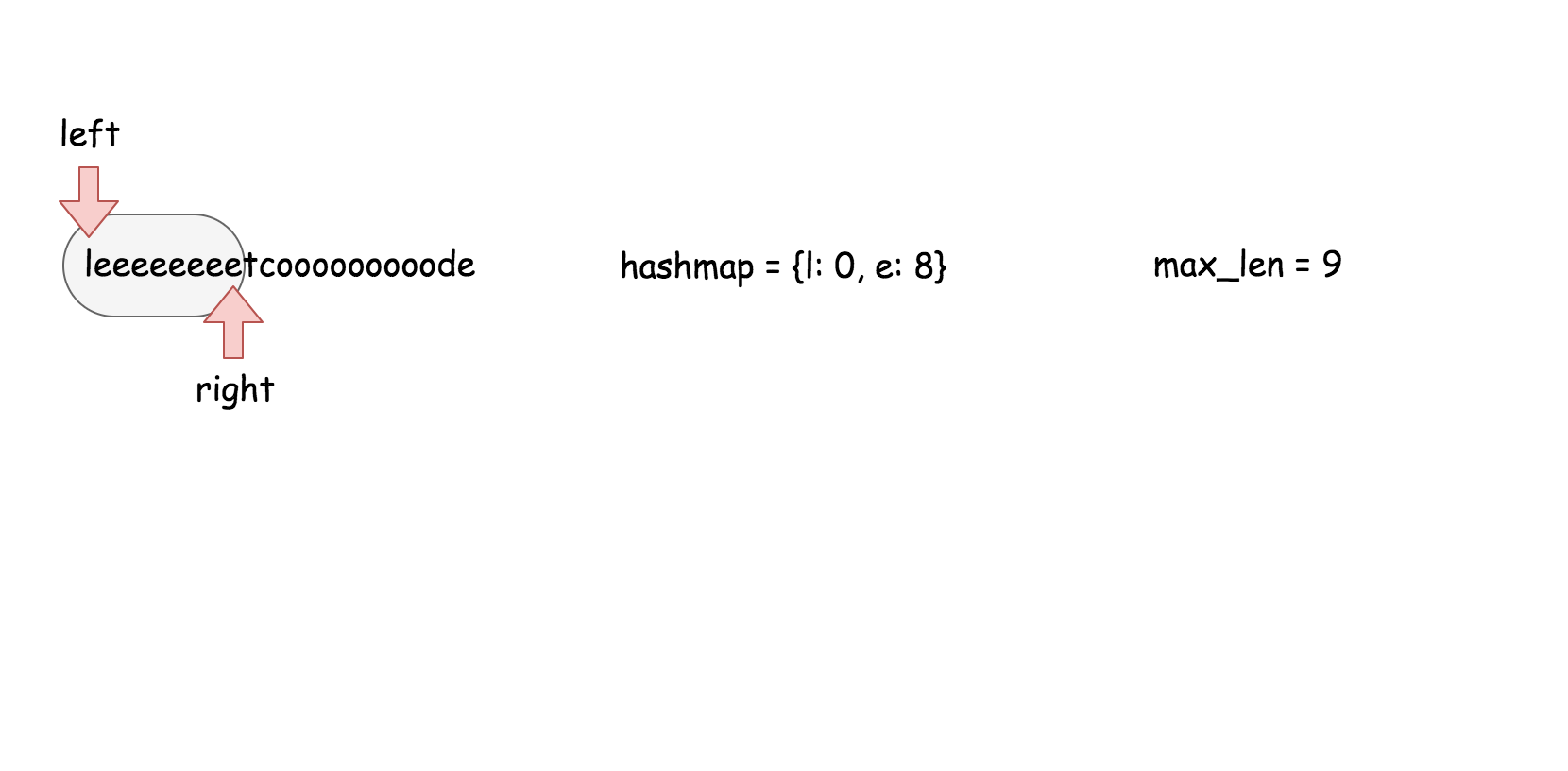,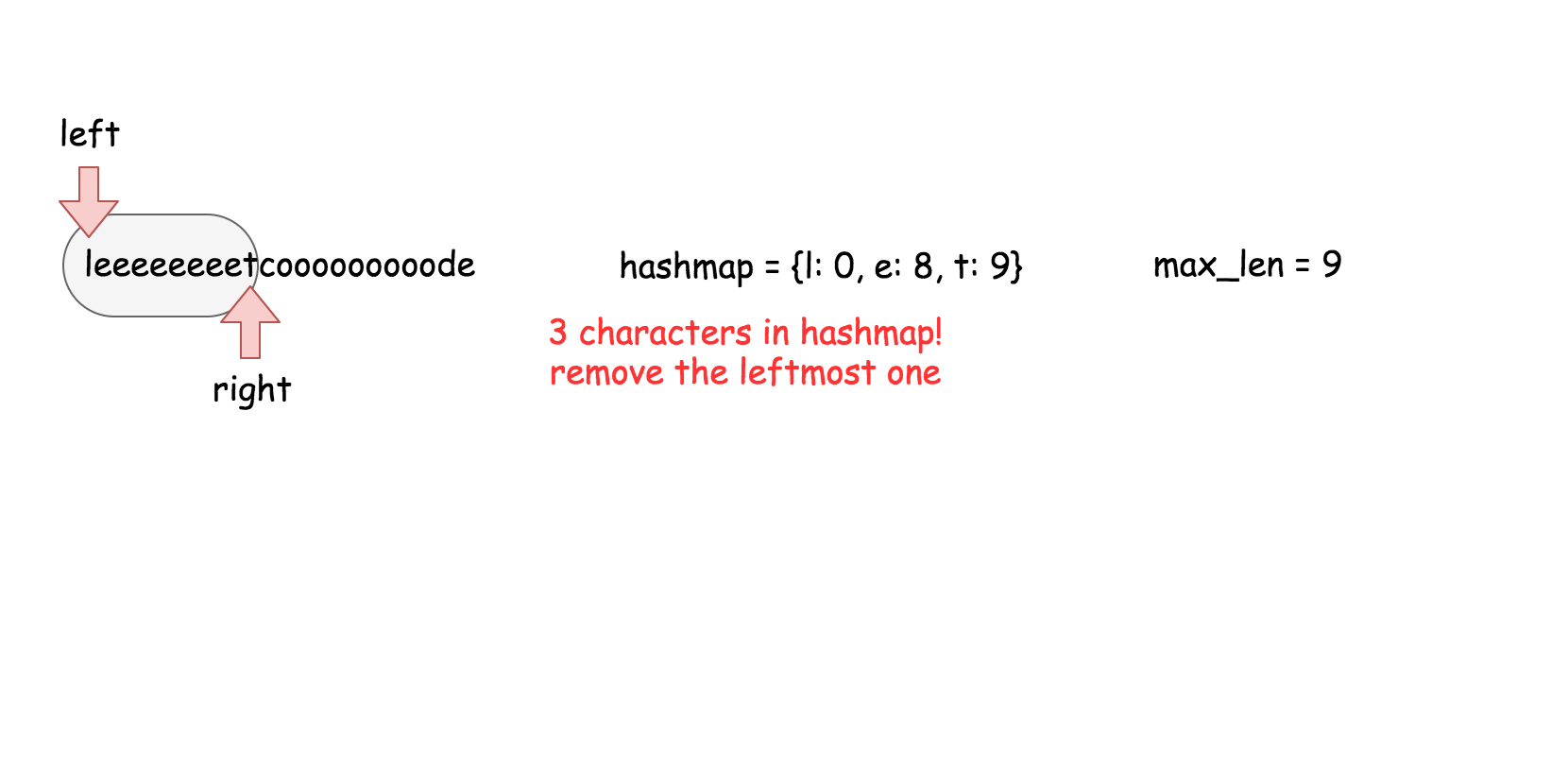,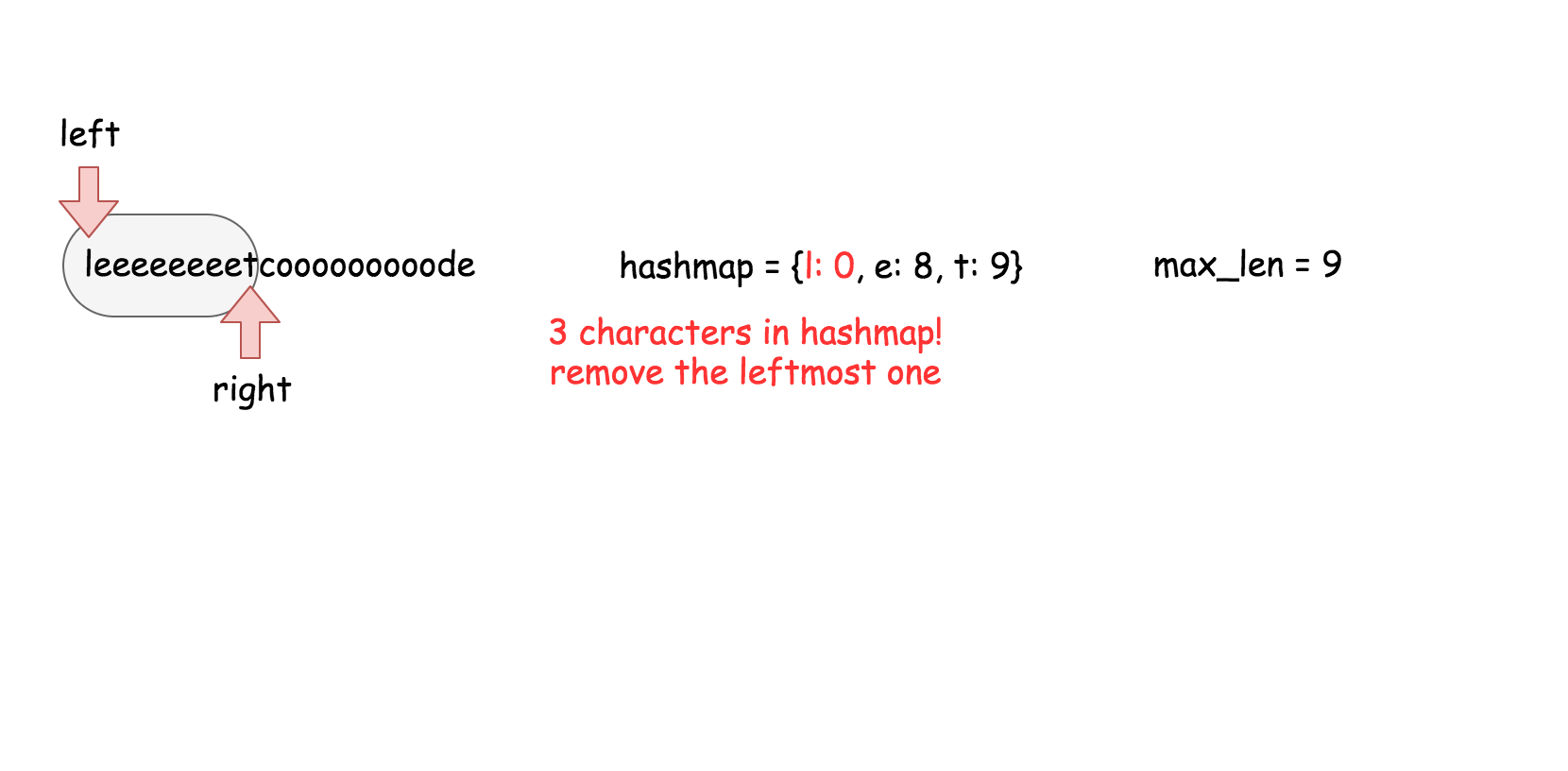,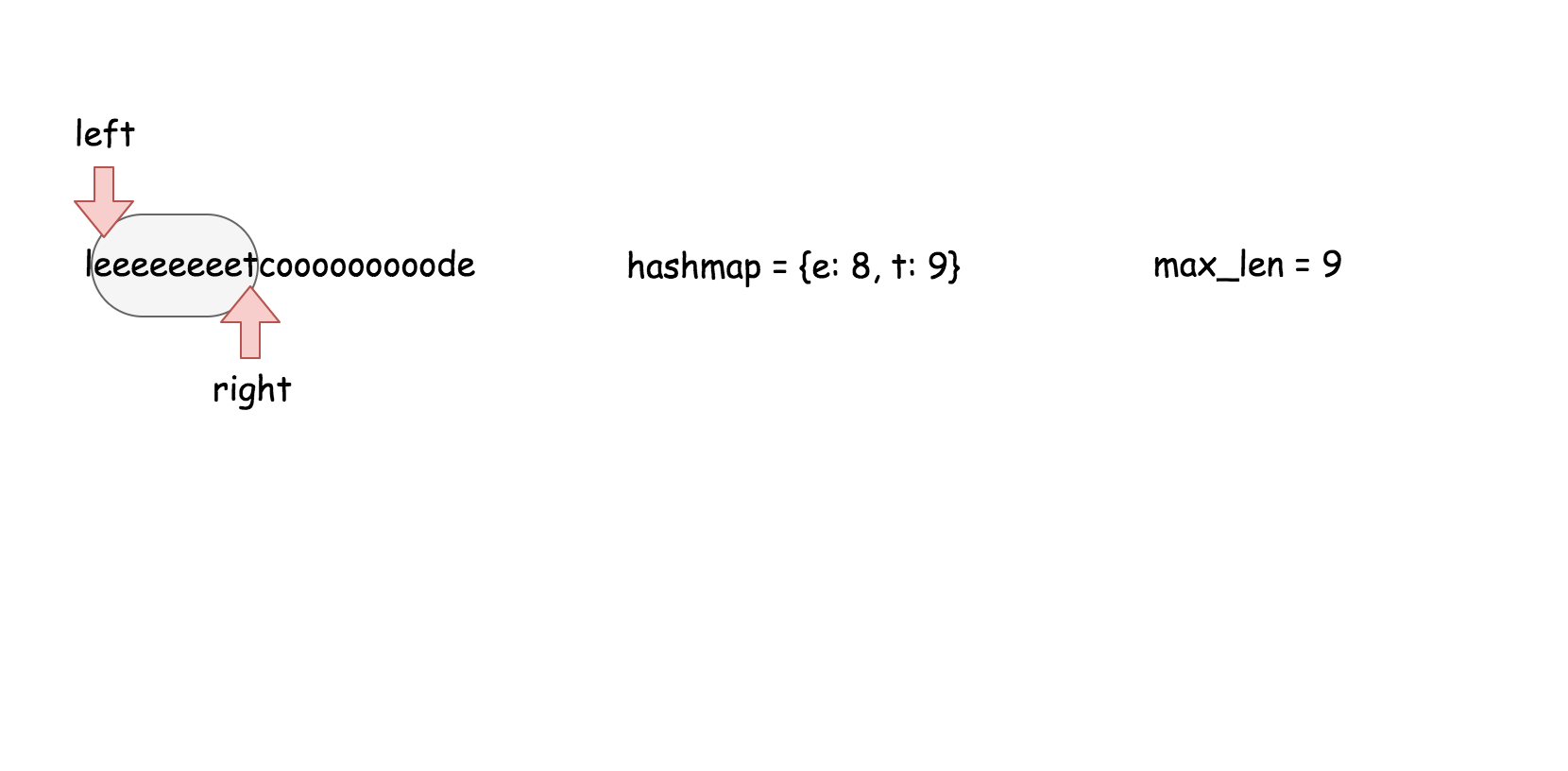,,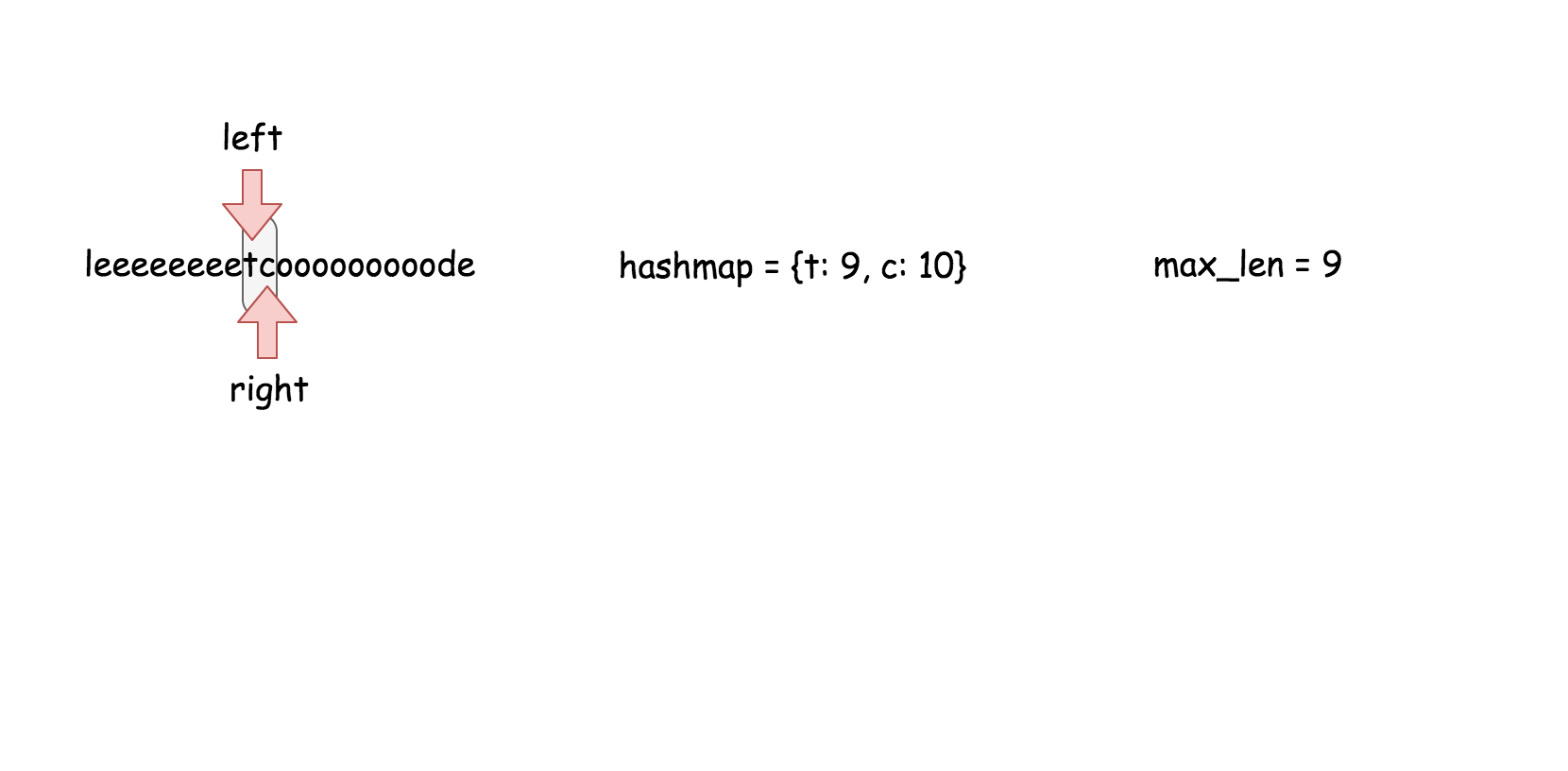,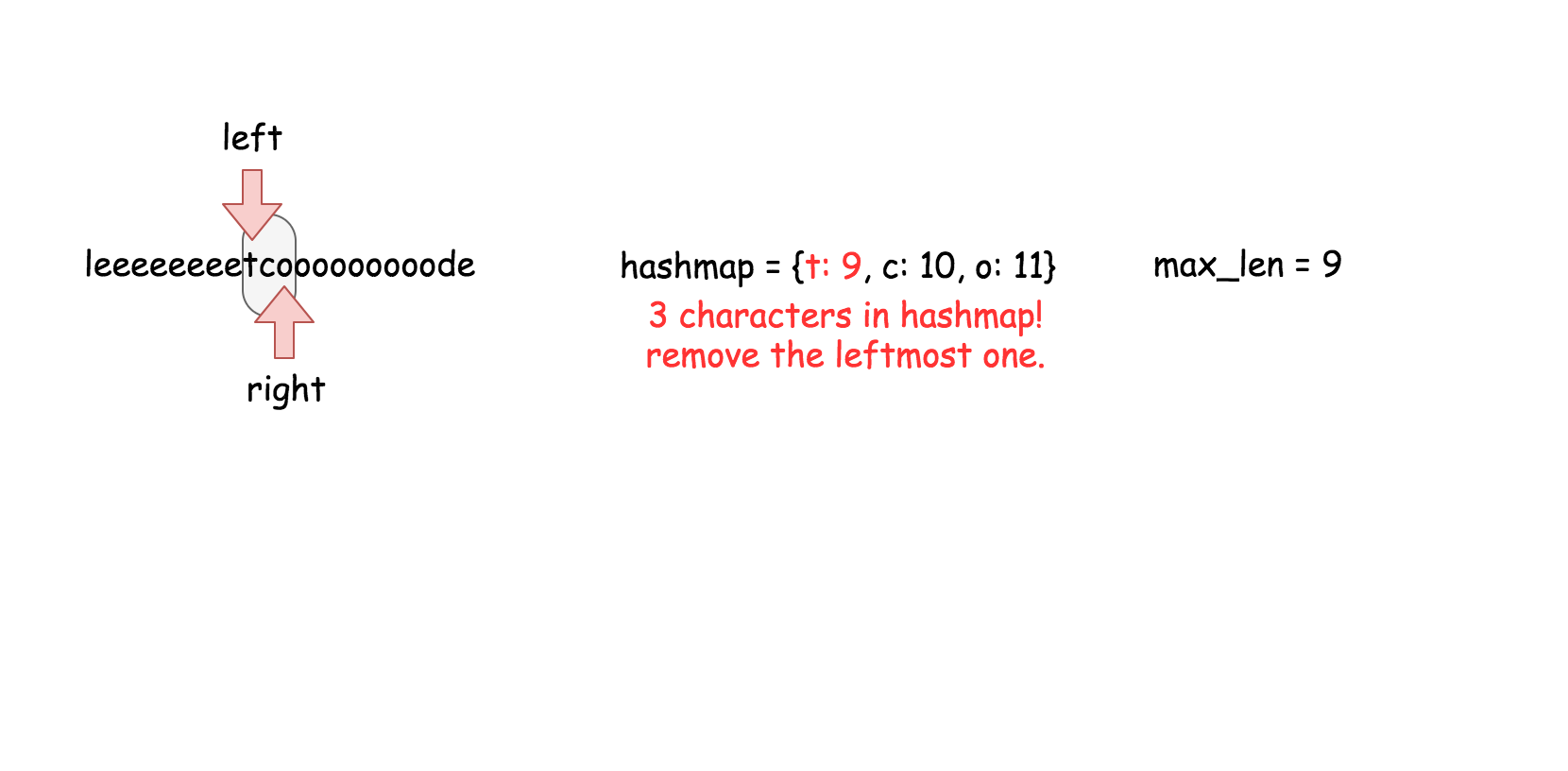,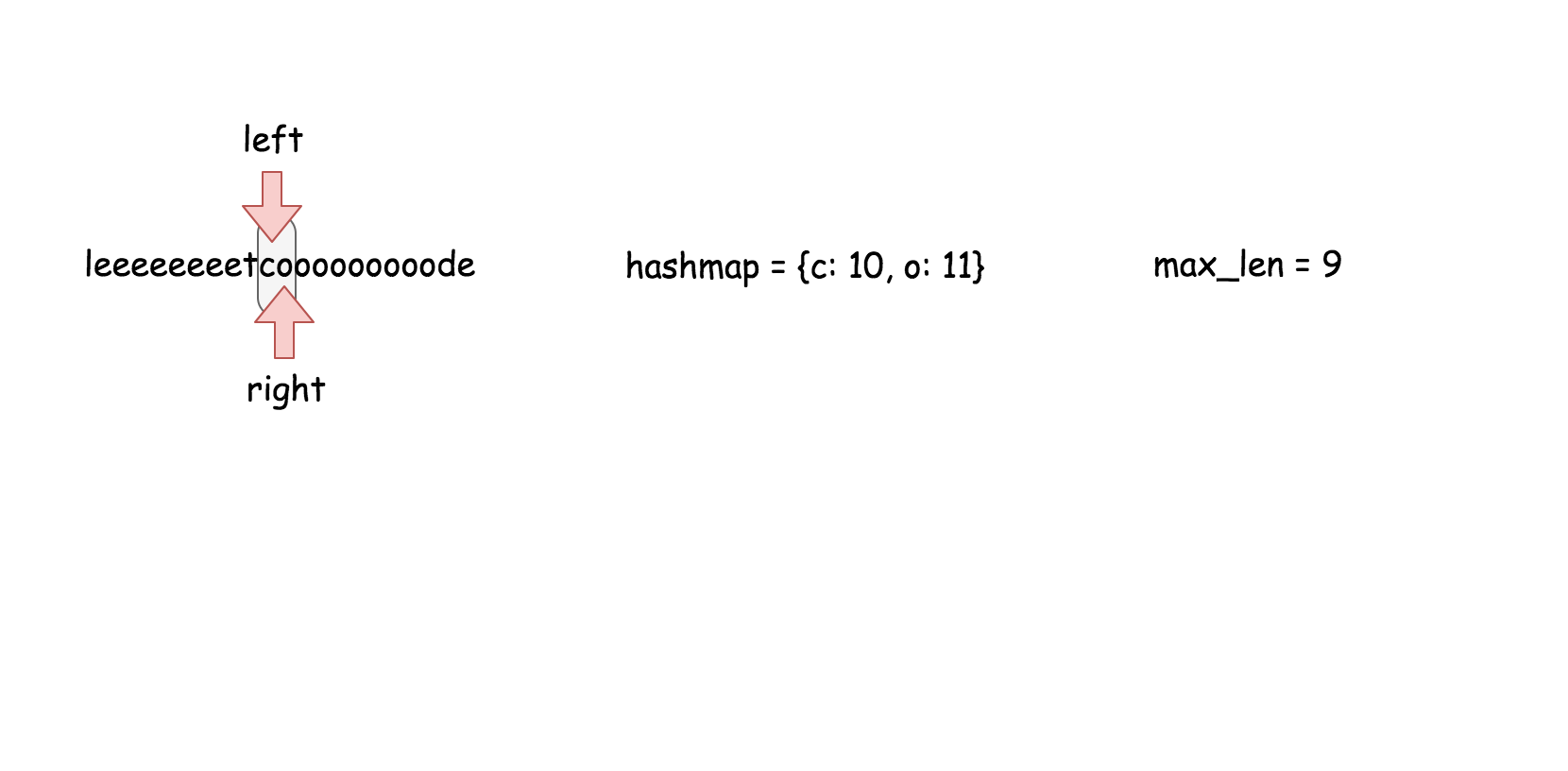,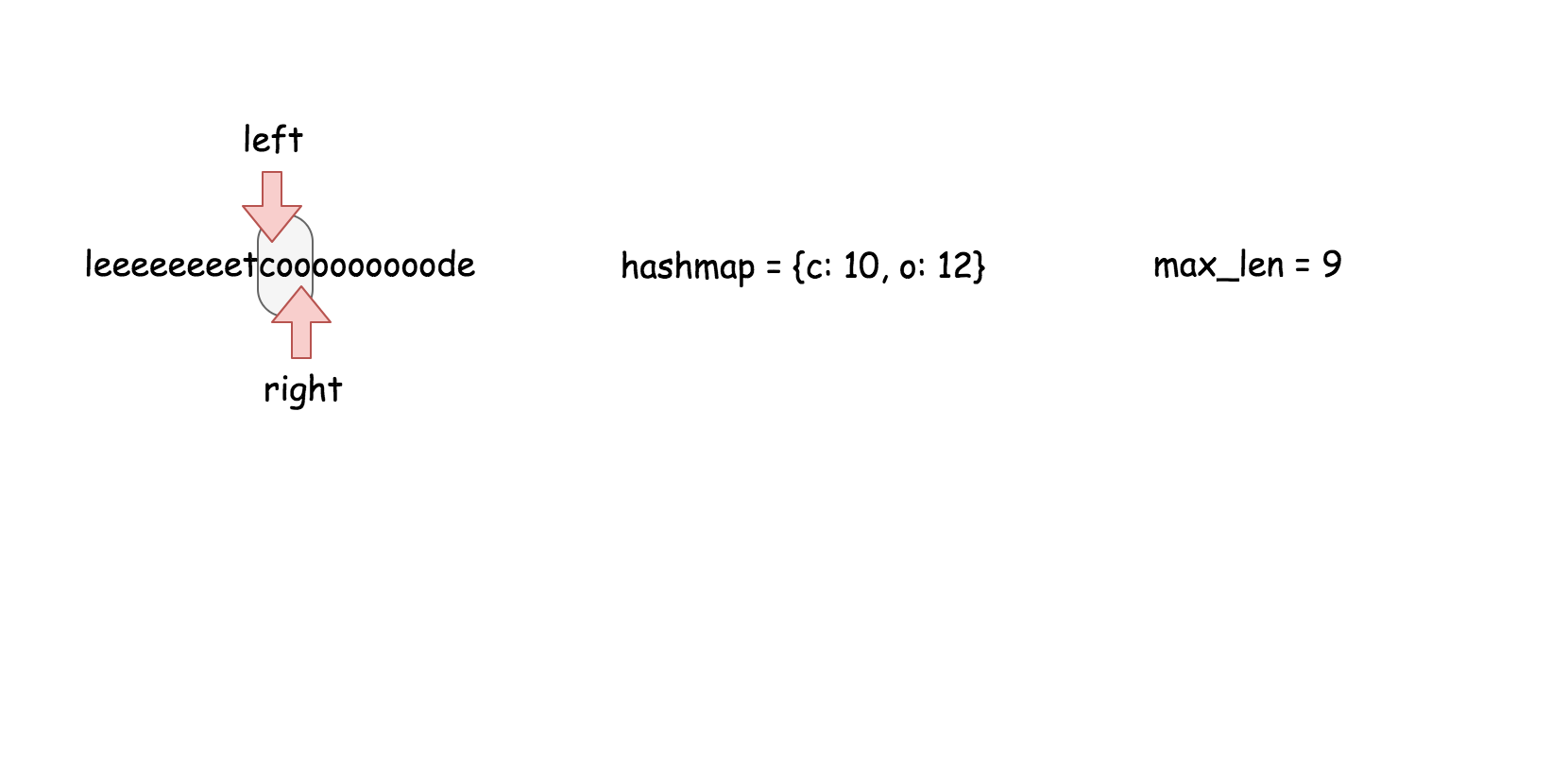,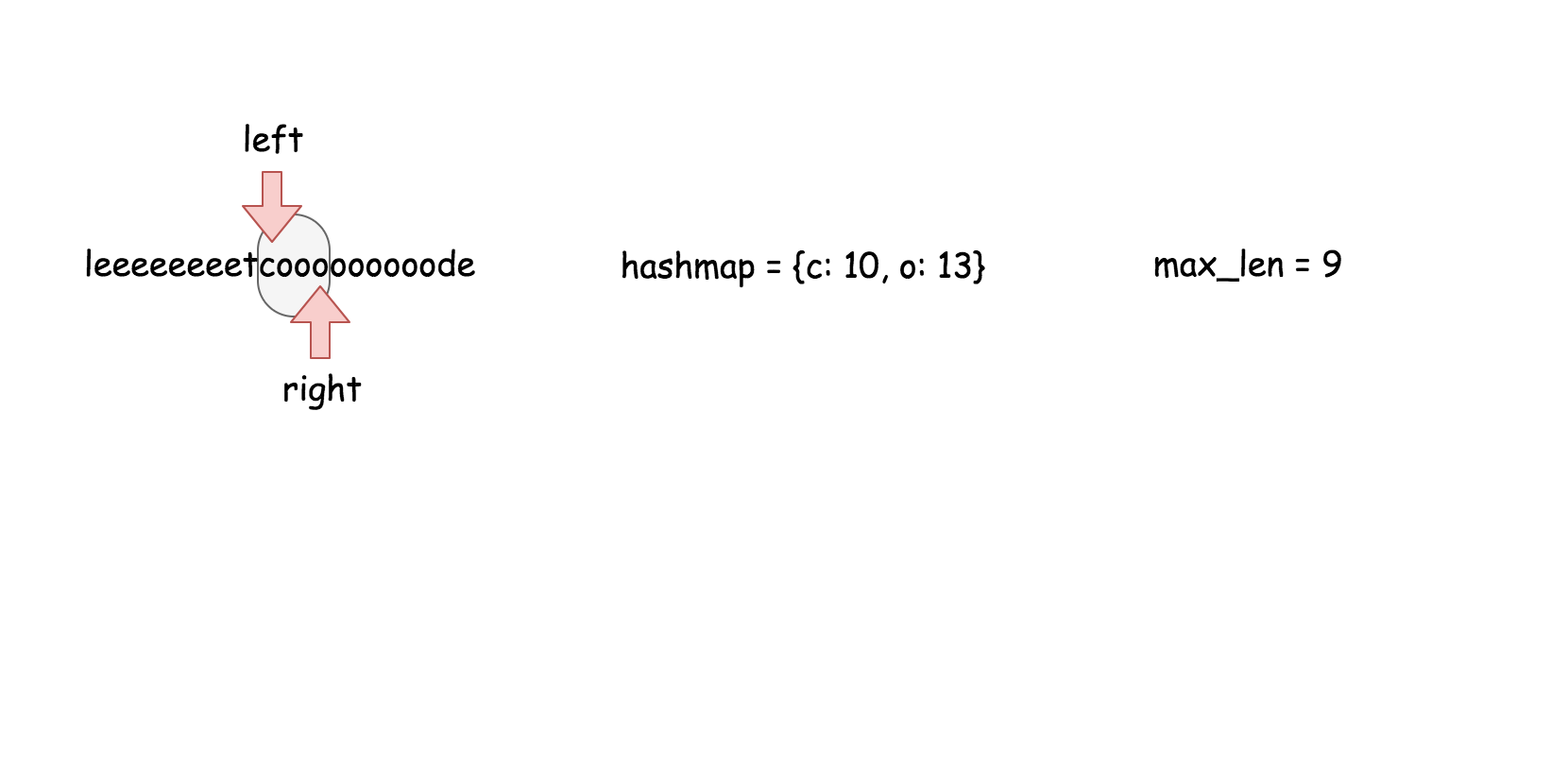,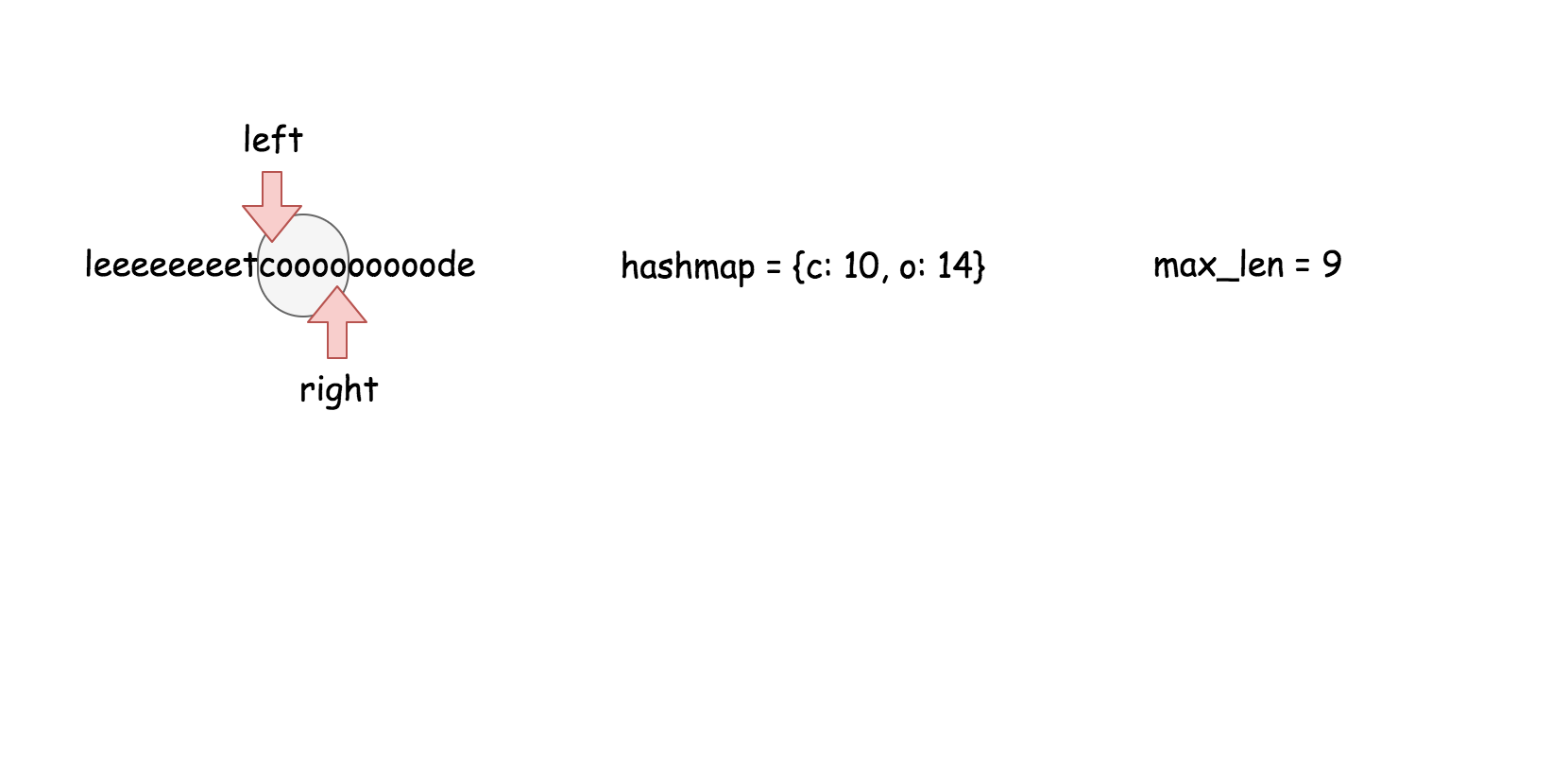,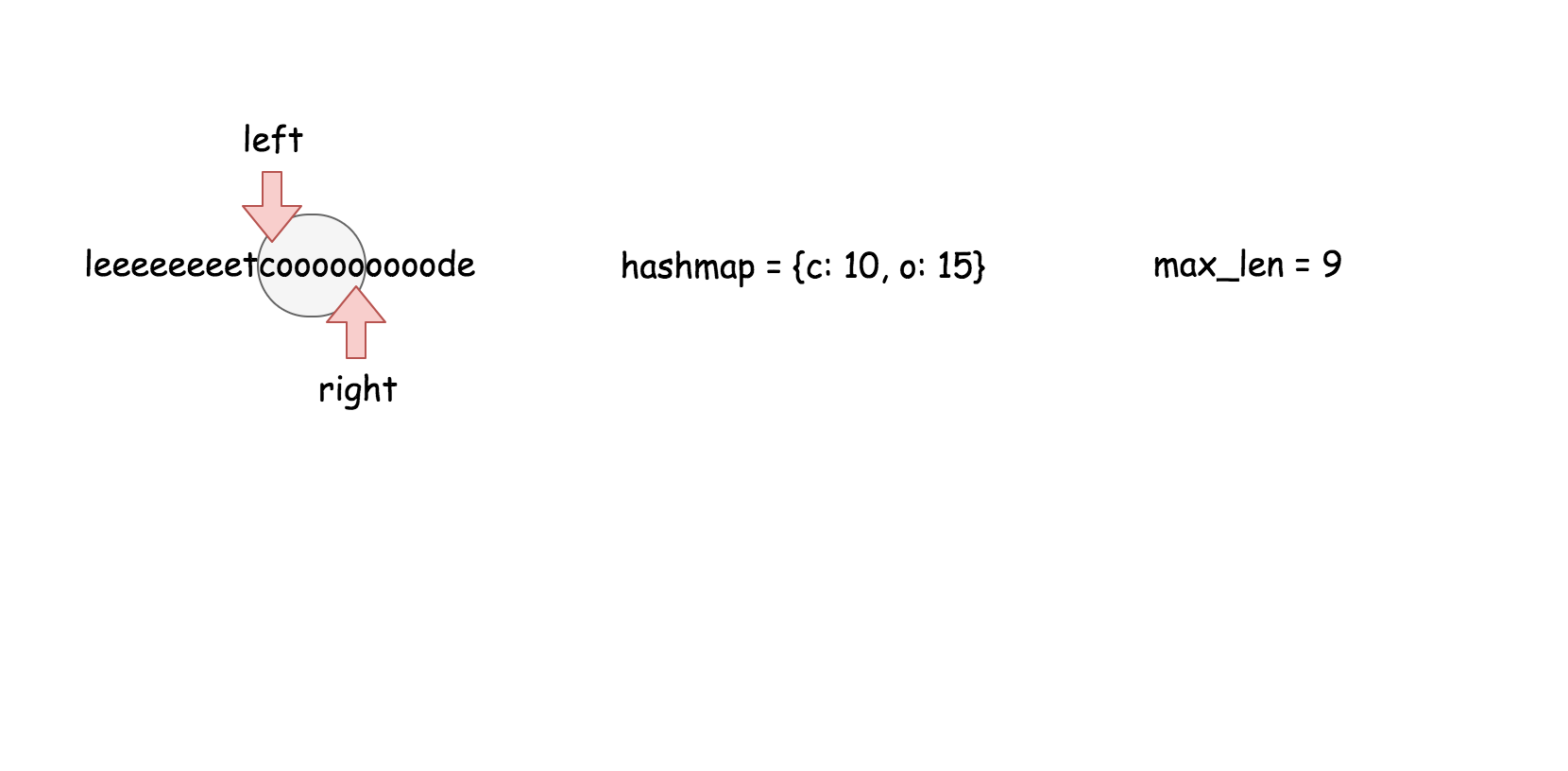,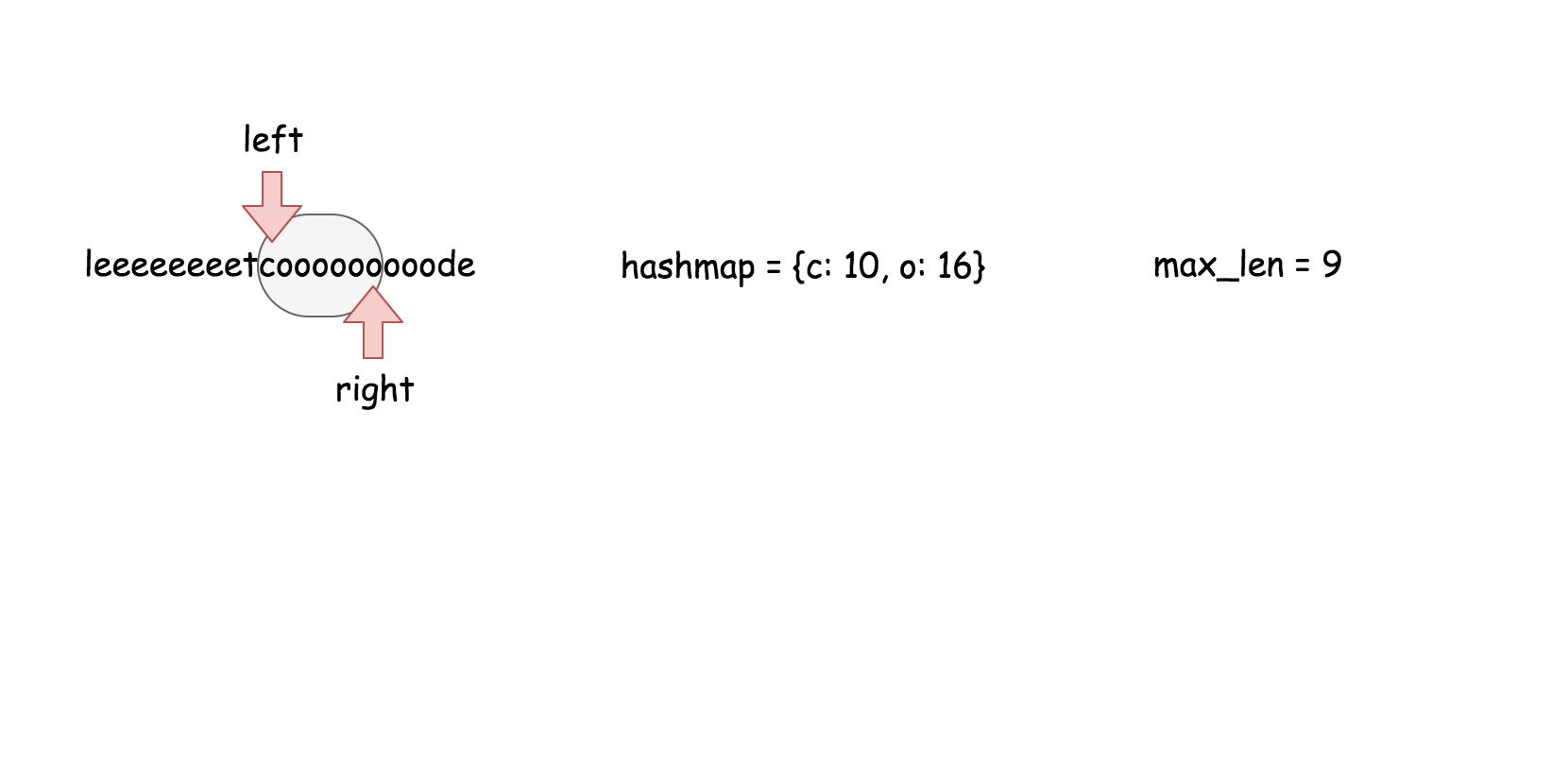,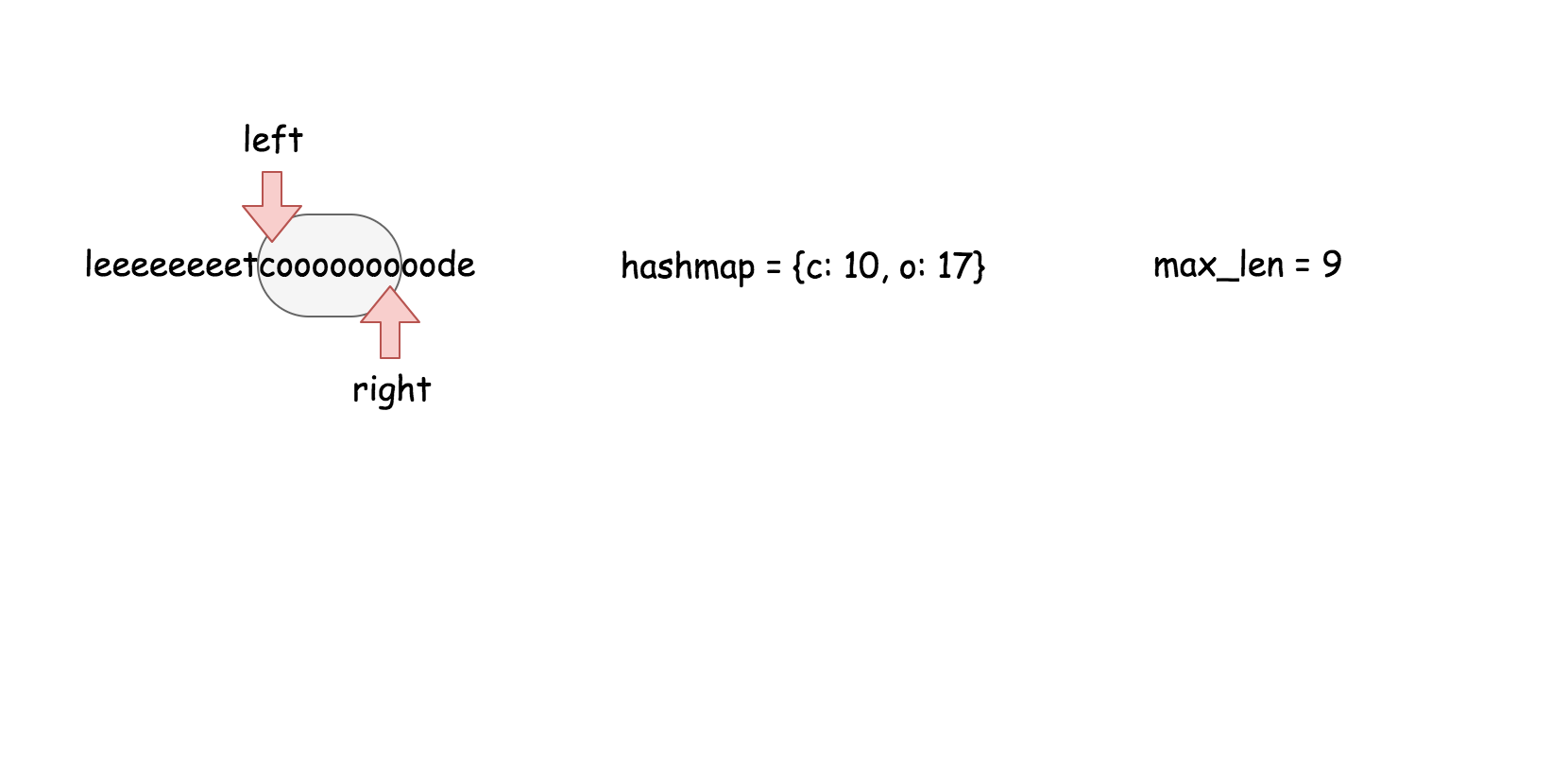,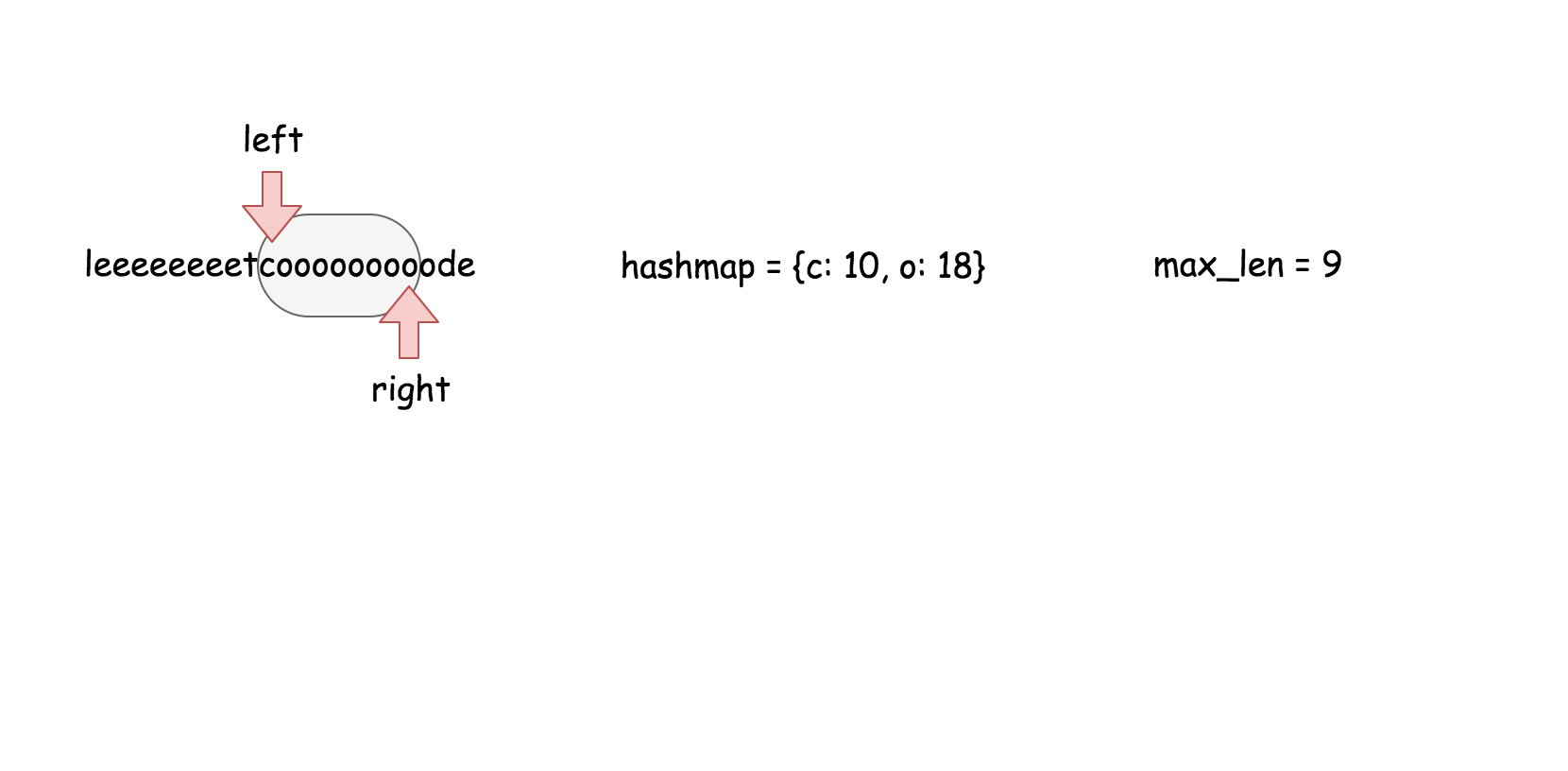,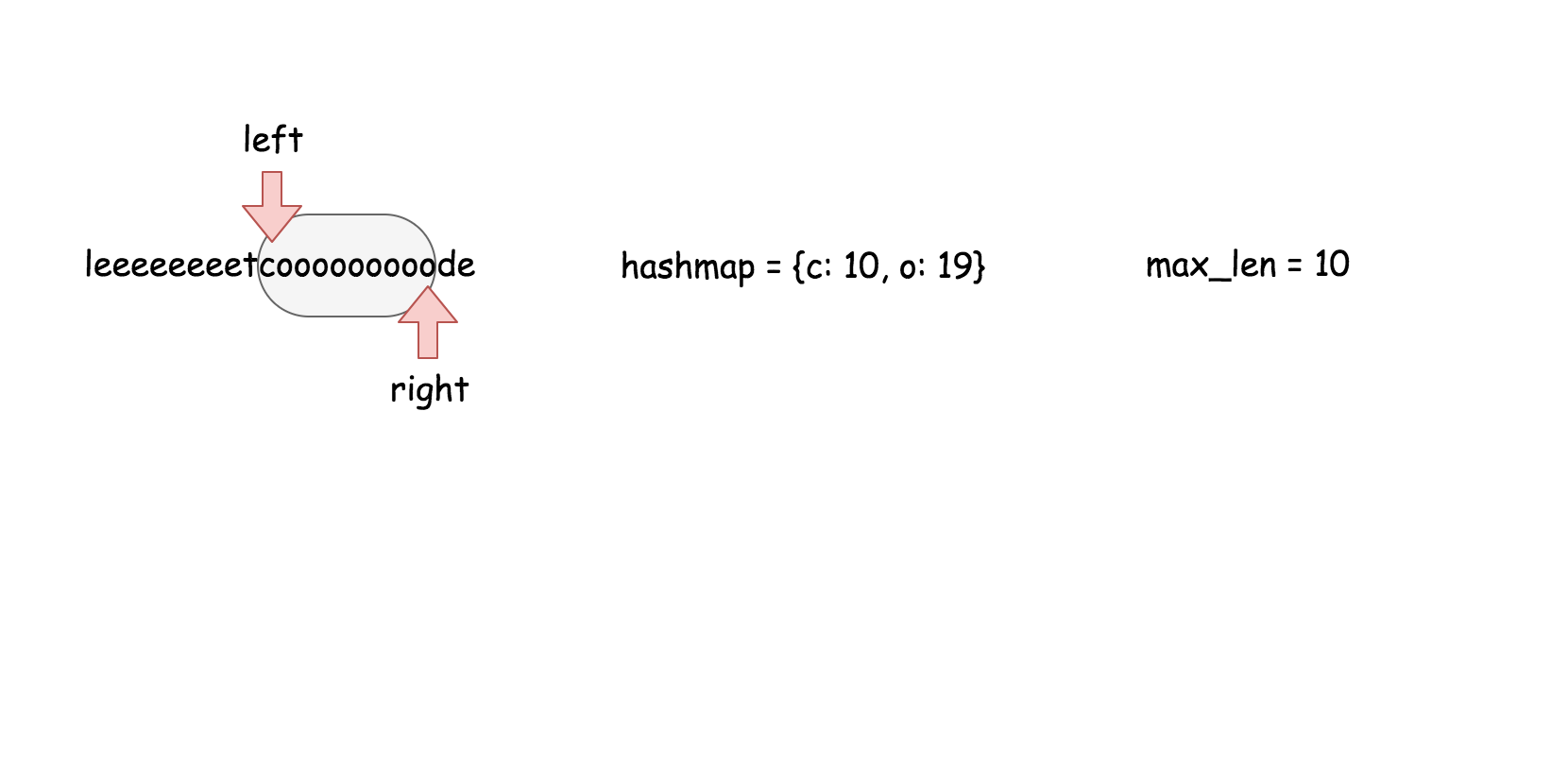,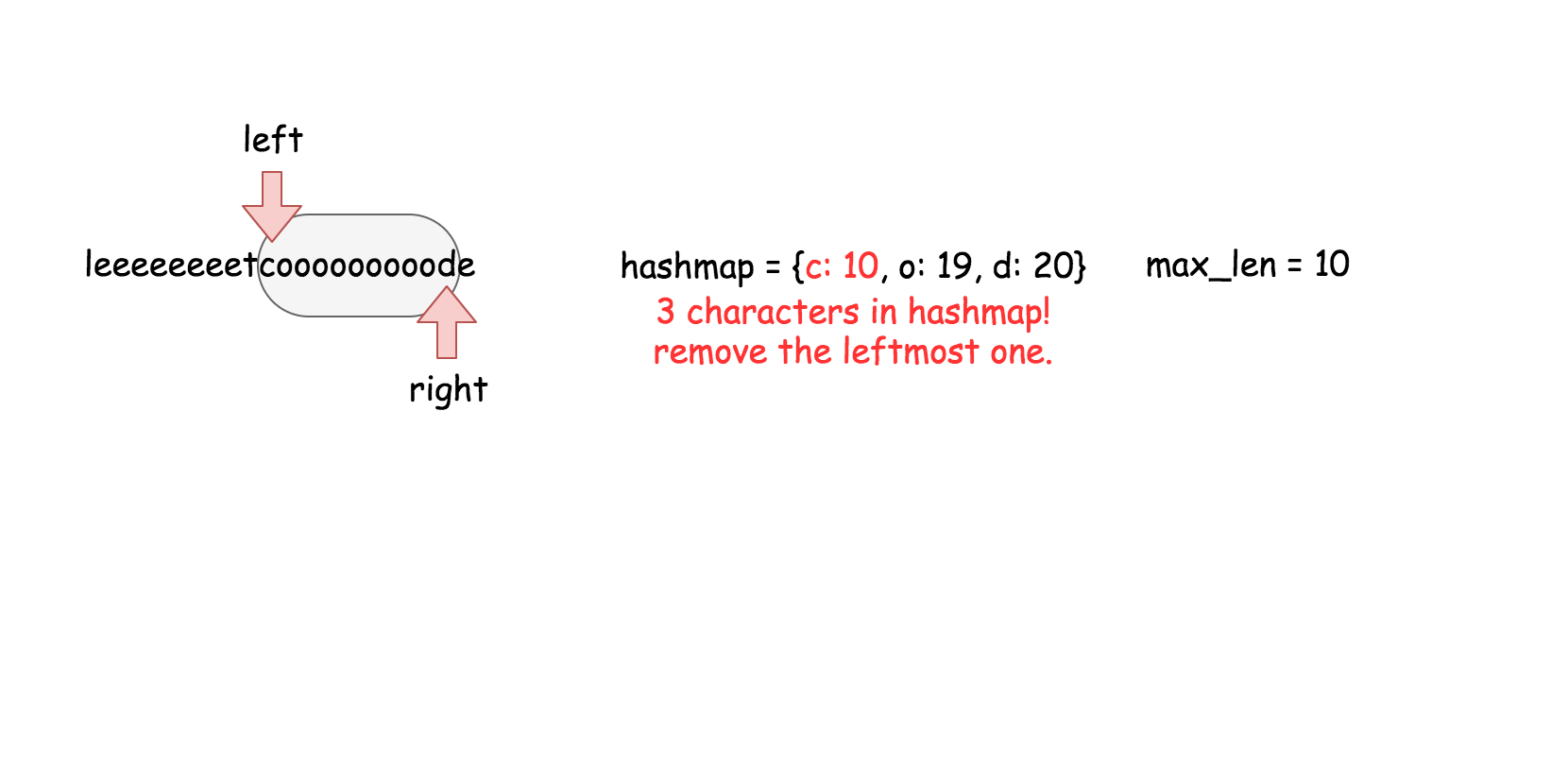,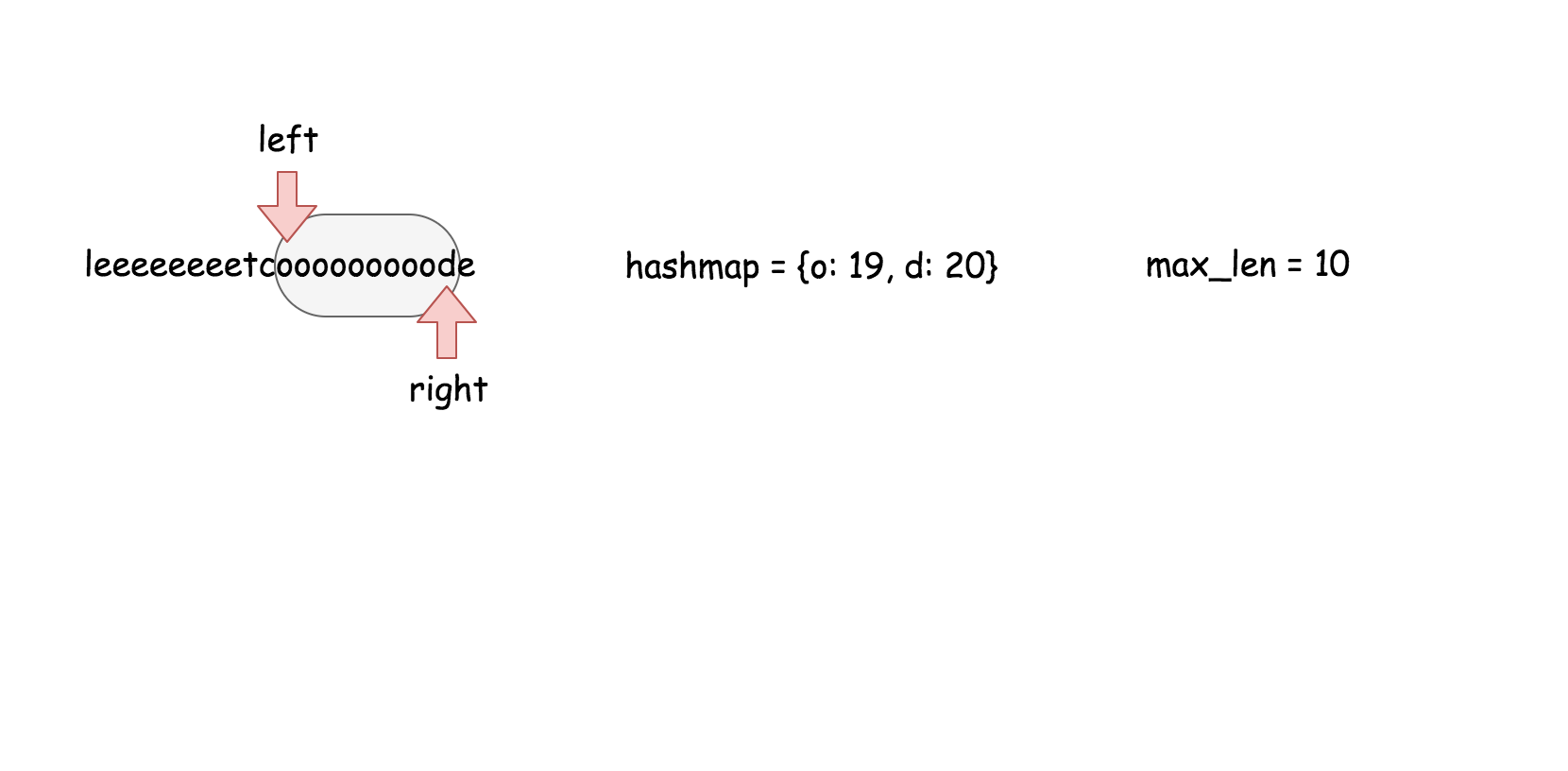,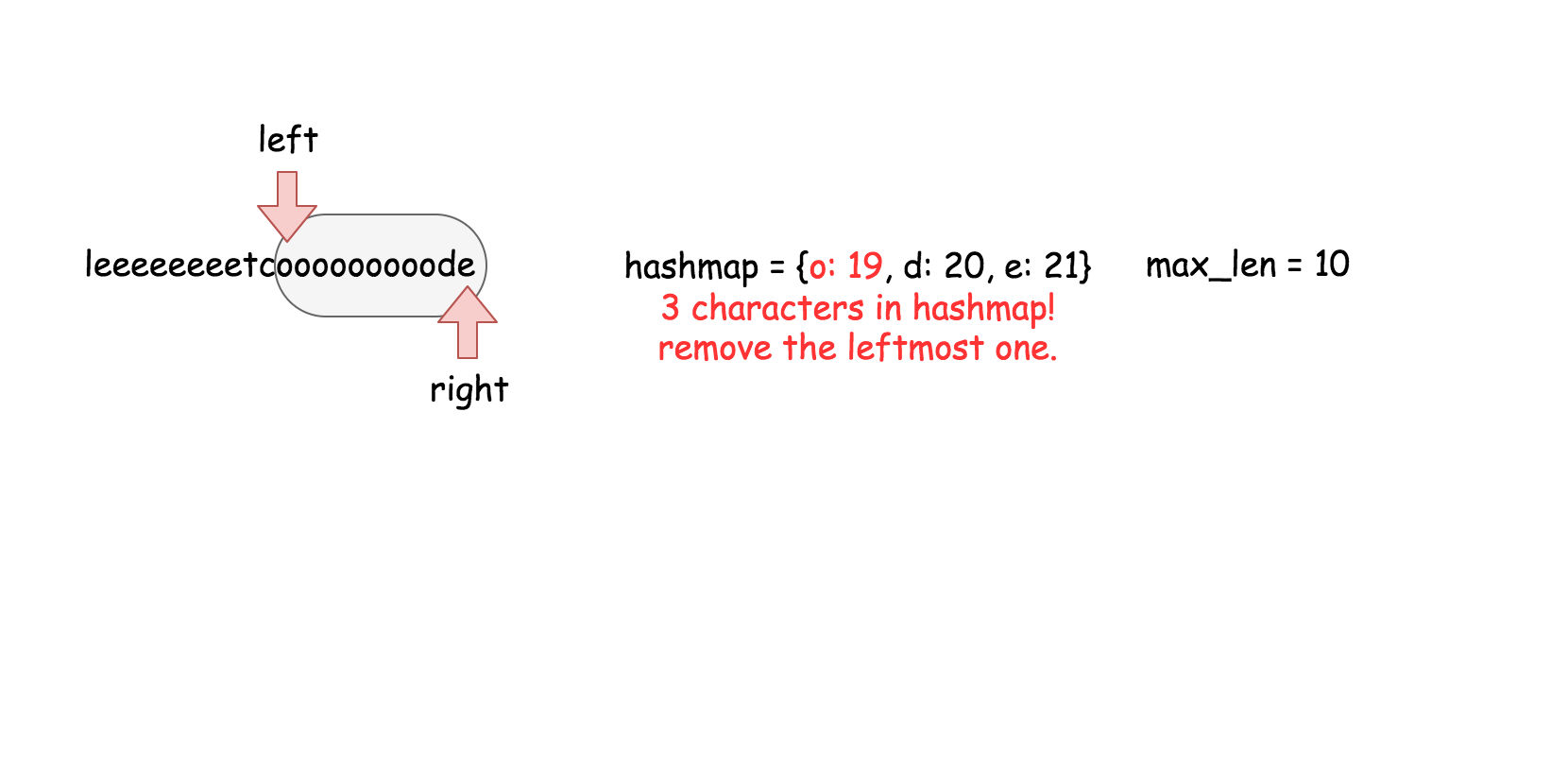,>
|
||||
|
||||
<br /> ```Java [] class Solution { public int lengthOfLongestSubstringTwoDistinct(String s) { int n = s.length(); if (n < 3) return n;
|
||||
|
||||
// sliding window left and right pointers
|
||||
int left = 0;
|
||||
int right = 0;
|
||||
// hashmap character -> its rightmost position
|
||||
// in the sliding window
|
||||
HashMap<Character, Integer> hashmap = new HashMap<Character, Integer>();
|
||||
|
||||
int max_len = 2;
|
||||
|
||||
while (right < n) {
|
||||
// slidewindow contains less than 3 characters
|
||||
if (hashmap.size() < 3)
|
||||
hashmap.put(s.charAt(right), right++);
|
||||
|
||||
// slidewindow contains 3 characters
|
||||
if (hashmap.size() == 3) {
|
||||
// delete the leftmost character
|
||||
int del_idx = Collections.min(hashmap.values());
|
||||
hashmap.remove(s.charAt(del_idx));
|
||||
// move left pointer of the slidewindow
|
||||
left = del_idx + 1;
|
||||
}
|
||||
|
||||
max_len = Math.max(max_len, right - left);
|
||||
}
|
||||
return max_len;
|
||||
|
||||
}
|
||||
}
|
||||
|
||||
*
|
||||
|
||||
```
|
||||
|
||||
```Python []
|
||||
from collections import defaultdict
|
||||
class Solution:
|
||||
def lengthOfLongestSubstringTwoDistinct(self, s: 'str') -> 'int':
|
||||
n = len(s)
|
||||
if n < 3:
|
||||
return n
|
||||
|
||||
# sliding window left and right pointers
|
||||
left, right = 0, 0
|
||||
# hashmap character -> its rightmost position
|
||||
# in the sliding window
|
||||
hashmap = defaultdict()
|
||||
|
||||
max_len = 2
|
||||
|
||||
while right < n:
|
||||
# slidewindow contains less than 3 characters
|
||||
if len(hashmap) < 3:
|
||||
hashmap[s[right]] = right
|
||||
right += 1
|
||||
|
||||
# slidewindow contains 3 characters
|
||||
if len(hashmap) == 3:
|
||||
# delete the leftmost character
|
||||
del_idx = min(hashmap.values())
|
||||
del hashmap[s[del_idx]]
|
||||
# move left pointer of the slidewindow
|
||||
left = del_idx + 1
|
||||
|
||||
max_len = max(max_len, right - left)
|
||||
|
||||
return max_len
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
* 时间复杂度:$\mathcal{O}(N)$ 其中 `N` 是输入串的字符数目。
|
||||
|
||||
* 空间复杂度:$\mathcal{O}(1)$,这是因为额外的空间只有 hashmap ,且它包含不超过 `3` 个元素。
|
||||
|
||||
**相似问题**
|
||||
|
||||
相同的滑动窗口问题还可以用来解决如下问题:[《340. 至多包含 K 个不同字符的最长子串》](https://leetcode-cn.com/problems/longest-substring-with-at-most-k-distinct-characters/)
|
||||
@ -0,0 +1,345 @@
|
||||
#### 方法一:哈希表
|
||||
|
||||
我们可以用一个哈希表统计 $s$ 所有长度为 $10$ 的子串的出现次数,返回所有出现次数超过 $10$ 的子串。
|
||||
|
||||
代码实现时,可以一边遍历子串一边记录答案,为了不重复记录答案,我们只统计当前出现次数为 $2$ 的子串。
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
L = 10
|
||||
|
||||
class Solution:
|
||||
def findRepeatedDnaSequences(self, s: str) -> List[str]:
|
||||
ans = []
|
||||
cnt = defaultdict(int)
|
||||
for i in range(len(s) - L + 1):
|
||||
sub = s[i : i + L]
|
||||
cnt[sub] += 1
|
||||
if cnt[sub] == 2:
|
||||
ans.append(sub)
|
||||
return ans
|
||||
```
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
const int L = 10;
|
||||
public:
|
||||
vector<string> findRepeatedDnaSequences(string s) {
|
||||
vector<string> ans;
|
||||
unordered_map<string, int> cnt;
|
||||
int n = s.length();
|
||||
for (int i = 0; i <= n - L; ++i) {
|
||||
string sub = s.substr(i, L);
|
||||
if (++cnt[sub] == 2) {
|
||||
ans.push_back(sub);
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
static final int L = 10;
|
||||
|
||||
public List<String> findRepeatedDnaSequences(String s) {
|
||||
List<String> ans = new ArrayList<String>();
|
||||
Map<String, Integer> cnt = new HashMap<String, Integer>();
|
||||
int n = s.length();
|
||||
for (int i = 0; i <= n - L; ++i) {
|
||||
String sub = s.substring(i, i + L);
|
||||
cnt.put(sub, cnt.getOrDefault(sub, 0) + 1);
|
||||
if (cnt.get(sub) == 2) {
|
||||
ans.add(sub);
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
const int L = 10;
|
||||
|
||||
public IList<string> FindRepeatedDnaSequences(string s) {
|
||||
IList<string> ans = new List<string>();
|
||||
Dictionary<string, int> cnt = new Dictionary<string, int>();
|
||||
int n = s.Length;
|
||||
for (int i = 0; i <= n - L; ++i) {
|
||||
string sub = s.Substring(i, L);
|
||||
if (!cnt.ContainsKey(sub)) {
|
||||
cnt.Add(sub, 1);
|
||||
} else {
|
||||
++cnt[sub];
|
||||
}
|
||||
if (cnt[sub] == 2) {
|
||||
ans.Add(sub);
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
const L = 10
|
||||
|
||||
func findRepeatedDnaSequences(s string) (ans []string) {
|
||||
cnt := map[string]int{}
|
||||
for i := 0; i <= len(s)-L; i++ {
|
||||
sub := s[i : i+L]
|
||||
cnt[sub]++
|
||||
if cnt[sub] == 2 {
|
||||
ans = append(ans, sub)
|
||||
}
|
||||
}
|
||||
return
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var findRepeatedDnaSequences = function(s) {
|
||||
const L = 10;
|
||||
const ans = [];
|
||||
const cnt = new Map();
|
||||
const n = s.length;
|
||||
for (let i = 0; i <= n - L; ++i) {
|
||||
const sub = s.slice(i, i + L)
|
||||
cnt.set(sub, (cnt.get(sub) || 0) + 1);
|
||||
if (cnt.get(sub) === 2) {
|
||||
ans.push(sub);
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(NL)$,其中 $N$ 是字符串 $\textit{s}$ 的长度,$L=10$ 即目标子串的长度。
|
||||
|
||||
- 空间复杂度:$O(NL)$。
|
||||
|
||||
#### 方法二:哈希表 + 滑动窗口 + 位运算
|
||||
|
||||
由于 $s$ 中只含有 $4$ 种字符,我们可以将每个字符用 $2$ 个比特表示,即:
|
||||
|
||||
- $\texttt{A}$ 表示为二进制 $\texttt{00}$;
|
||||
- $\texttt{C}$ 表示为二进制 $\texttt{01}$;
|
||||
- $\texttt{G}$ 表示为二进制 $\texttt{10}$;
|
||||
- $\texttt{T}$ 表示为二进制 $\texttt{11}$。
|
||||
|
||||
如此一来,一个长为 $10$ 的字符串就可以用 $20$ 个比特表示,而一个 $\texttt{int}$ 整数有 $32$ 个比特,足够容纳该字符串,因此我们可以将 $s$ 的每个长为 $10$ 的子串用一个 $\texttt{int}$ 整数表示(只用低 $20$ 位)。
|
||||
|
||||
注意到上述字符串到整数的映射是一一映射,每个整数都对应着一个唯一的字符串,因此我们可以将方法一中的哈希表改为存储每个长为 $10$ 的子串的整数表示。
|
||||
|
||||
如果我们对每个长为 $10$ 的子串都单独计算其整数表示,那么时间复杂度仍然和方法一一样为 $O(NL)$。为了优化时间复杂度,我们可以用一个大小固定为 $10$ 的滑动窗口来计算子串的整数表示。设当前滑动窗口对应的整数表示为 $x$,当我们要计算下一个子串时,就将滑动窗口向右移动一位,此时会有一个新的字符进入窗口,以及窗口最左边的字符离开窗口,这些操作对应的位运算,按计算顺序表示如下:
|
||||
|
||||
- 滑动窗口向右移动一位:`x = x << 2`,由于每个字符用 $2$ 个比特表示,所以要左移 $2$ 位;
|
||||
- 一个新的字符 $\textit{ch}$ 进入窗口:`x = x | bin[ch]`,这里 $\textit{bin}[\textit{ch}]$ 为字符 $\textit{ch}$ 的对应二进制;
|
||||
- 窗口最左边的字符离开窗口:`x = x & ((1 << 20) - 1)`,由于我们只考虑 $x$ 的低 $20$ 位比特,需要将其余位置零,即与上 `(1 << 20) - 1`。
|
||||
|
||||
将这三步合并,就可以用 $O(1)$ 的时间计算出下一个子串的整数表示,即 `x = ((x << 2) | bin[ch]) & ((1 << 20) - 1)`。
|
||||
|
||||
* [sol2-Python3]
|
||||
|
||||
```Python
|
||||
L = 10
|
||||
bin = {'A': 0, 'C': 1, 'G': 2, 'T': 3}
|
||||
|
||||
class Solution:
|
||||
def findRepeatedDnaSequences(self, s: str) -> List[str]:
|
||||
n = len(s)
|
||||
if n <= L:
|
||||
return []
|
||||
ans = []
|
||||
x = 0
|
||||
for ch in s[:L - 1]:
|
||||
x = (x << 2) | bin[ch]
|
||||
cnt = defaultdict(int)
|
||||
for i in range(n - L + 1):
|
||||
x = ((x << 2) | bin[s[i + L - 1]]) & ((1 << (L * 2)) - 1)
|
||||
cnt[x] += 1
|
||||
if cnt[x] == 2:
|
||||
ans.append(s[i : i + L])
|
||||
return ans
|
||||
```
|
||||
|
||||
* [sol2-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
const int L = 10;
|
||||
unordered_map<char, int> bin = {{'A', 0}, {'C', 1}, {'G', 2}, {'T', 3}};
|
||||
public:
|
||||
vector<string> findRepeatedDnaSequences(string s) {
|
||||
vector<string> ans;
|
||||
int n = s.length();
|
||||
if (n <= L) {
|
||||
return ans;
|
||||
}
|
||||
int x = 0;
|
||||
for (int i = 0; i < L - 1; ++i) {
|
||||
x = (x << 2) | bin[s[i]];
|
||||
}
|
||||
unordered_map<int, int> cnt;
|
||||
for (int i = 0; i <= n - L; ++i) {
|
||||
x = ((x << 2) | bin[s[i + L - 1]]) & ((1 << (L * 2)) - 1);
|
||||
if (++cnt[x] == 2) {
|
||||
ans.push_back(s.substr(i, L));
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
static final int L = 10;
|
||||
Map<Character, Integer> bin = new HashMap<Character, Integer>() {{
|
||||
put('A', 0);
|
||||
put('C', 1);
|
||||
put('G', 2);
|
||||
put('T', 3);
|
||||
}};
|
||||
|
||||
public List<String> findRepeatedDnaSequences(String s) {
|
||||
List<String> ans = new ArrayList<String>();
|
||||
int n = s.length();
|
||||
if (n <= L) {
|
||||
return ans;
|
||||
}
|
||||
int x = 0;
|
||||
for (int i = 0; i < L - 1; ++i) {
|
||||
x = (x << 2) | bin.get(s.charAt(i));
|
||||
}
|
||||
Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();
|
||||
for (int i = 0; i <= n - L; ++i) {
|
||||
x = ((x << 2) | bin.get(s.charAt(i + L - 1))) & ((1 << (L * 2)) - 1);
|
||||
cnt.put(x, cnt.getOrDefault(x, 0) + 1);
|
||||
if (cnt.get(x) == 2) {
|
||||
ans.add(s.substring(i, i + L));
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
const int L = 10;
|
||||
Dictionary<char, int> bin = new Dictionary<char, int> {
|
||||
{'A', 0}, {'C', 1}, {'G', 2}, {'T', 3}
|
||||
};
|
||||
|
||||
public IList<string> FindRepeatedDnaSequences(string s) {
|
||||
IList<string> ans = new List<string>();
|
||||
int n = s.Length;
|
||||
if (n <= L) {
|
||||
return ans;
|
||||
}
|
||||
int x = 0;
|
||||
for (int i = 0; i < L - 1; ++i) {
|
||||
x = (x << 2) | bin[s[i]];
|
||||
}
|
||||
Dictionary<int, int> cnt = new Dictionary<int, int>();
|
||||
for (int i = 0; i <= n - L; ++i) {
|
||||
x = ((x << 2) | bin[s[i + L - 1]]) & ((1 << (L * 2)) - 1);
|
||||
if (!cnt.ContainsKey(x)) {
|
||||
cnt.Add(x, 1);
|
||||
} else {
|
||||
++cnt[x];
|
||||
}
|
||||
if (cnt[x] == 2) {
|
||||
ans.Add(s.Substring(i, L));
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Golang]
|
||||
|
||||
```go
|
||||
const L = 10
|
||||
var bin = map[byte]int{'A': 0, 'C': 1, 'G': 2, 'T': 3}
|
||||
|
||||
func findRepeatedDnaSequences(s string) (ans []string) {
|
||||
n := len(s)
|
||||
if n <= L {
|
||||
return
|
||||
}
|
||||
x := 0
|
||||
for _, ch := range s[:L-1] {
|
||||
x = x<<2 | bin[byte(ch)]
|
||||
}
|
||||
cnt := map[int]int{}
|
||||
for i := 0; i <= n-L; i++ {
|
||||
x = (x<<2 | bin[s[i+L-1]]) & (1<<(L*2) - 1)
|
||||
cnt[x]++
|
||||
if cnt[x] == 2 {
|
||||
ans = append(ans, s[i:i+L])
|
||||
}
|
||||
}
|
||||
return ans
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var findRepeatedDnaSequences = function(s) {
|
||||
const L = 10;
|
||||
const bin = new Map();
|
||||
bin.set('A', 0);
|
||||
bin.set('C', 1);
|
||||
bin.set('G', 2);
|
||||
bin.set('T', 3);
|
||||
|
||||
const ans = [];
|
||||
const n = s.length;
|
||||
if (n <= L) {
|
||||
return ans;
|
||||
}
|
||||
let x = 0;
|
||||
for (let i = 0; i < L - 1; ++i) {
|
||||
x = (x << 2) | bin.get(s[i]);
|
||||
}
|
||||
const cnt = new Map();
|
||||
for (let i = 0; i <= n - L; ++i) {
|
||||
x = ((x << 2) | bin.get(s[i + L - 1])) & ((1 << (L * 2)) - 1);
|
||||
cnt.set(x, (cnt.get(x) || 0) + 1);
|
||||
if (cnt.get(x) === 2) {
|
||||
ans.push(s.slice(i, i + L));
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
};
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(N)$,其中 $N$ 是字符串 $\textit{s}$ 的长度。
|
||||
|
||||
- 空间复杂度:$O(N)$。
|
||||
|
||||
@ -0,0 +1,88 @@
|
||||
本题很直接可以想到前缀树+DFS的思路,不过要注意一点神坑:测试用例的字典中可能包含重复的单词。应对这点,只需要在字典树结点中加上条件count用于统计相同单词的出现次数即可。
|
||||
|
||||
也可以不直接建树,先将字典单词排序,每次遍历前缀符合的单词,保留集合以供下一轮遍历。多次重复遍历即可得出结果。
|
||||
|
||||
* java
|
||||
|
||||
```java
|
||||
public class SearchSuggestionsSystem {
|
||||
private class TrieNode{
|
||||
boolean end = false;
|
||||
String str = null;
|
||||
int count = 0;
|
||||
TrieNode[] children = new TrieNode[26];
|
||||
}
|
||||
|
||||
private class Trie{
|
||||
TrieNode root = new TrieNode();
|
||||
public void insert(String[] products){
|
||||
for(String str : products){
|
||||
insertWord(str);
|
||||
}
|
||||
}
|
||||
private void insertWord(String products){
|
||||
TrieNode node = root;
|
||||
for(char c : products.toCharArray()){
|
||||
if(node.children[c - 'a'] == null){
|
||||
node.children[c - 'a'] = new TrieNode();
|
||||
}
|
||||
node = node.children[c - 'a'];
|
||||
}
|
||||
if(node.end != true){
|
||||
node.end = true;
|
||||
node.str = products;
|
||||
}
|
||||
node.count++;
|
||||
}
|
||||
public List<List<String>> searchWord(String word){
|
||||
List<List<String>> result = new ArrayList<>();
|
||||
for(int i = 1; i <= word.length(); i++){
|
||||
result.add(search(word.substring(0, i)));
|
||||
}
|
||||
return result;
|
||||
}
|
||||
private List<String> search(String pattern){
|
||||
List<String> result = new ArrayList<>();
|
||||
TrieNode node = root;
|
||||
for(char c : pattern.toCharArray()){
|
||||
if(node.children[c - 'a'] == null){
|
||||
return result;
|
||||
}
|
||||
node = node.children[c - 'a'];
|
||||
}
|
||||
Solution(node, result);
|
||||
return result;
|
||||
}
|
||||
private void Solution(TrieNode root, List<String> result){
|
||||
if(root.end){
|
||||
for(int i = 0; i < root.count; i++){
|
||||
result.add(root.str);
|
||||
if(result.size() == 3){
|
||||
return;
|
||||
}
|
||||
}
|
||||
}
|
||||
for(TrieNode node : root.children){
|
||||
if(node != null){
|
||||
Solution(node, result);
|
||||
}
|
||||
if(result.size() == 3){
|
||||
return;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public List<List<String>> suggestedProducts(String[] products, String searchWord) {
|
||||
Trie trie = new Trie();
|
||||
trie.insert(products);
|
||||
return trie.searchWord(searchWord);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
欢迎与我交流~
|
||||
|
||||
[LeetCode 从零单刷个人笔记整理(持续更新)](https://blog.csdn.net/qq_20304723/article/details/89401203)
|
||||
|
||||
github:[https://github.com/ChopinXBP/LeetCode-Babel](https://github.com/ChopinXBP/LeetCode-Babel)
|
||||
@ -0,0 +1,362 @@
|
||||
#### 前言
|
||||
|
||||
对于数组 $A$ 的区间 $[\textit{left}, \textit{right}]$ 而言,只要它包含不超过 $k$ 个 $0$,我们就可以根据它构造出一段满足要求,并且长度为 $\textit{right} - \textit{left} + 1$ 的区间。
|
||||
|
||||
因此,我们可以将该问题进行如下的转化,即:
|
||||
|
||||
> 对于任意的右端点 $\textit{right}$,希望找到最小的左端点 $\textit{left}$,使得 $[\textit{left}, \textit{right}]$ 包含不超过 $k$ 个 $0$。
|
||||
>
|
||||
> 只要我们枚举所有可能的右端点,将得到的区间的长度取最大值,即可得到答案。
|
||||
|
||||
要想快速判断一个区间内 $0$ 的个数,我们可以考虑将数组 $A$ 中的 $0$ 变成 $1$,$1$ 变成 $0$。此时,我们对数组 $A$ 求出前缀和,记为数组 $P$,那么 $[\textit{left}, \textit{right}]$ 中包含不超过 $k$ 个 $1$(注意这里就不是 $0$ 了),当且仅当二者的前缀和之差:
|
||||
|
||||
$$
|
||||
P[\textit{right}] - P[\textit{left} - 1]
|
||||
$$
|
||||
|
||||
小于等于 $k$。这样一来,我们就可以容易地解决这个问题了。
|
||||
|
||||
#### 方法一:二分查找
|
||||
|
||||
**思路与算法**
|
||||
|
||||
$$
|
||||
P[\textit{right}] - P[\textit{left} - 1] \leq k
|
||||
$$
|
||||
|
||||
等价于
|
||||
|
||||
$$
|
||||
P[\textit{left} - 1] \geq P[\textit{right}] - k \tag{1}
|
||||
$$
|
||||
|
||||
也就是说,我们需要找到最小的满足 $(1)$ 式的 $\textit{left}$。由于数组 $A$ 中仅包含 $0/1$,因此前缀和数组是一个单调递增的数组,我们就可以使用二分查找的方法得到 $\textit{left}$。
|
||||
|
||||
**细节**
|
||||
|
||||
注意到 $(1)$ 式的左侧的下标是 $\textit{left}-1$ 而不是 $\textit{left}$,那么我们在构造前缀和数组时,可以将前缀和整体向右移动一位,空出 $P[0]$ 的位置,即:
|
||||
|
||||
$$
|
||||
\begin
|
||||
P[0] = 0 \\
|
||||
P[i] = P[i-1] + (1 - A[i-1])
|
||||
\end
|
||||
$$
|
||||
|
||||
此时,我们在数组 $P$ 上二分查找到的下标即为 $\textit{left}$ 本身,同时我们也避免了原先 $\textit{left}=0$ 时 $\textit{left}-1=-1$ 不在数组合法的下标范围中的边界情况。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int longestOnes(vector<int>& nums, int k) {
|
||||
int n = nums.size();
|
||||
vector<int> P(n + 1);
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
P[i] = P[i - 1] + (1 - nums[i - 1]);
|
||||
}
|
||||
|
||||
int ans = 0;
|
||||
for (int right = 0; right < n; ++right) {
|
||||
int left = lower_bound(P.begin(), P.end(), P[right + 1] - k) - P.begin();
|
||||
ans = max(ans, right - left + 1);
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int longestOnes(int[] nums, int k) {
|
||||
int n = nums.length;
|
||||
int[] P = new int[n + 1];
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
P[i] = P[i - 1] + (1 - nums[i - 1]);
|
||||
}
|
||||
|
||||
int ans = 0;
|
||||
for (int right = 0; right < n; ++right) {
|
||||
int left = binarySearch(P, P[right + 1] - k);
|
||||
ans = Math.max(ans, right - left + 1);
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
|
||||
public int binarySearch(int[] P, int target) {
|
||||
int low = 0, high = P.length - 1;
|
||||
while (low < high) {
|
||||
int mid = (high - low) / 2 + low;
|
||||
if (P[mid] < target) {
|
||||
low = mid + 1;
|
||||
} else {
|
||||
high = mid;
|
||||
}
|
||||
}
|
||||
return low;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def longestOnes(self, nums: List[int], k: int) -> int:
|
||||
n = len(nums)
|
||||
P = [0]
|
||||
for num in nums:
|
||||
P.append(P[-1] + (1 - num))
|
||||
|
||||
ans = 0
|
||||
for right in range(n):
|
||||
left = bisect.bisect_left(P, P[right + 1] - k)
|
||||
ans = max(ans, right - left + 1)
|
||||
|
||||
return ans
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var longestOnes = function(nums, k) {
|
||||
const n = nums.length;
|
||||
const P = new Array(n + 1).fill(0);
|
||||
for (let i = 1; i <= n; ++i) {
|
||||
P[i] = P[i - 1] + (1 - nums[i - 1]);
|
||||
}
|
||||
|
||||
let ans = 0;
|
||||
for (let right = 0; right < n; ++right) {
|
||||
const left = binarySearch(P, P[right + 1] - k);
|
||||
ans = Math.max(ans, right - left + 1);
|
||||
}
|
||||
return ans;
|
||||
};
|
||||
|
||||
const binarySearch = (P, target) => {
|
||||
let low = 0, high = P.length - 1;
|
||||
while (low < high) {
|
||||
const mid = Math.floor((high - low) / 2) + low;
|
||||
if (P[mid] < target) {
|
||||
low = mid + 1;
|
||||
} else {
|
||||
high = mid;
|
||||
}
|
||||
}
|
||||
return low;
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func longestOnes(nums []int, k int) (ans int) {
|
||||
n := len(nums)
|
||||
P := make([]int, n+1)
|
||||
for i, v := range nums {
|
||||
P[i+1] = P[i] + 1 - v
|
||||
}
|
||||
for right, v := range P {
|
||||
left := sort.SearchInts(P, v-k)
|
||||
ans = max(ans, right-left)
|
||||
}
|
||||
return
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
int binarySearch(int* P, int len, int target) {
|
||||
int low = 0, high = len - 1;
|
||||
while (low < high) {
|
||||
int mid = (high - low) / 2 + low;
|
||||
if (P[mid] < target) {
|
||||
low = mid + 1;
|
||||
} else {
|
||||
high = mid;
|
||||
}
|
||||
}
|
||||
return low;
|
||||
}
|
||||
|
||||
int longestOnes(int* nums, int numsSize, int k) {
|
||||
int P[numsSize + 1];
|
||||
P[0] = 0;
|
||||
for (int i = 1; i <= numsSize; ++i) {
|
||||
P[i] = P[i - 1] + (1 - nums[i - 1]);
|
||||
}
|
||||
|
||||
int ans = 0;
|
||||
for (int right = 0; right < numsSize; ++right) {
|
||||
int left = binarySearch(P, numsSize + 1, P[right + 1] - k);
|
||||
ans = fmax(ans, right - left + 1);
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n \log n)$,其中 $n$ 是数组 $A$ 的长度。每一次二分查找的时间复杂度为 $O(\log n)$,我们需要枚举 $\textit{right}$ 进行 $n$ 次二分查找,因此总时间复杂度为 $O(n \log n)$。
|
||||
|
||||
- 空间复杂度:$O(n)$,即为前缀和数组 $P$ 需要的空间。
|
||||
|
||||
#### 方法二:滑动窗口
|
||||
|
||||
**思路与算法**
|
||||
|
||||
我们继续观察 $(1)$ 式,由于前缀和数组 $P$ 是单调递增的,那么 $(1)$ 式的右侧 $P[\textit{right}] - k$ 同样也是单调递增的。因此,我们可以发现:
|
||||
|
||||
> 随着 $\textit{right}$ 的增大,满足 $(1)$ 式的最小的 $\textit{left}$ 值是单调递增的。
|
||||
|
||||
这样一来,我们就可以使用滑动窗口来实时地维护 $\textit{left}$ 和 $\textit{right}$ 了。在 $\textit{right}$ 向右移动的过程中,我们同步移动 $\textit{left}$,直到 $\textit{left}$ 为首个(即最小的)满足 $(1)$ 式的位置,此时我们就可以使用此区间对答案进行更新了。
|
||||
|
||||
**细节**
|
||||
|
||||
当我们使用滑动窗口代替二分查找解决本题时,就不需要显式地计算并保存出前缀和数组了。我们只需要知道 $\textit{left}$ 和 $\textit{right}$ 作为下标在前缀和数组中对应的值,因此我们只需要用两个变量 $\textit{lsum}$ 和 $\textit{rsum}$ 记录 $\textit{left}$ 和 $\textit{right}$ 分别对应的前缀和即可。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol2-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int longestOnes(vector<int>& nums, int k) {
|
||||
int n = nums.size();
|
||||
int left = 0, lsum = 0, rsum = 0;
|
||||
int ans = 0;
|
||||
for (int right = 0; right < n; ++right) {
|
||||
rsum += 1 - nums[right];
|
||||
while (lsum < rsum - k) {
|
||||
lsum += 1 - nums[left];
|
||||
++left;
|
||||
}
|
||||
ans = max(ans, right - left + 1);
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int longestOnes(int[] nums, int k) {
|
||||
int n = nums.length;
|
||||
int left = 0, lsum = 0, rsum = 0;
|
||||
int ans = 0;
|
||||
for (int right = 0; right < n; ++right) {
|
||||
rsum += 1 - nums[right];
|
||||
while (lsum < rsum - k) {
|
||||
lsum += 1 - nums[left];
|
||||
++left;
|
||||
}
|
||||
ans = Math.max(ans, right - left + 1);
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def longestOnes(self, nums: List[int], k: int) -> int:
|
||||
n = len(nums)
|
||||
left = lsum = rsum = 0
|
||||
ans = 0
|
||||
|
||||
for right in range(n):
|
||||
rsum += 1 - nums[right]
|
||||
while lsum < rsum - k:
|
||||
lsum += 1 - nums[left]
|
||||
left += 1
|
||||
ans = max(ans, right - left + 1)
|
||||
|
||||
return ans
|
||||
```
|
||||
|
||||
* [sol2-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var longestOnes = function(nums, k) {
|
||||
const n = nums.length;
|
||||
let left = 0, lsum = 0, rsum = 0;
|
||||
let ans = 0;
|
||||
for (let right = 0; right < n; ++right) {
|
||||
rsum += 1 - nums[right];
|
||||
while (lsum < rsum - k) {
|
||||
lsum += 1 - nums[left];
|
||||
++left;
|
||||
}
|
||||
ans = Math.max(ans, right - left + 1);
|
||||
}
|
||||
return ans;
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-Golang]
|
||||
|
||||
```go
|
||||
func longestOnes(nums []int, k int) (ans int) {
|
||||
var left, lsum, rsum int
|
||||
for right, v := range nums {
|
||||
rsum += 1 - v
|
||||
for lsum < rsum-k {
|
||||
lsum += 1 - nums[left]
|
||||
left++
|
||||
}
|
||||
ans = max(ans, right-left+1)
|
||||
}
|
||||
return
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-C]
|
||||
|
||||
```C
|
||||
int longestOnes(int* nums, int numsSize, int k) {
|
||||
int left = 0, lsum = 0, rsum = 0;
|
||||
int ans = 0;
|
||||
for (int right = 0; right < numsSize; ++right) {
|
||||
rsum += 1 - nums[right];
|
||||
while (lsum < rsum - k) {
|
||||
lsum += 1 - nums[left];
|
||||
++left;
|
||||
}
|
||||
ans = fmax(ans, right - left + 1);
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(n)$,其中 $n$ 是数组 $A$ 的长度。我们至多只需要遍历该数组两次(左右指针各一次)。
|
||||
|
||||
- 空间复杂度:$O(1)$,我们只需要常数的空间保存若干变量。
|
||||
|
||||
@ -0,0 +1,222 @@
|
||||
#### 方法一:数学
|
||||
|
||||
**思路及解法**
|
||||
|
||||
假设正整数 $n$ 在 $k~(k \geq 2)$ 进制下的所有数位都为 $1$,且位数为 $m + 1$,那么有:
|
||||
|
||||
$$
|
||||
n = k^0 + k^1 + k^2 + \dots + k^m\tag{1}
|
||||
$$
|
||||
|
||||
我们首先讨论两种特殊情况:
|
||||
|
||||
- $m=0$,此时 $n=1$,而题目保证 $n \geq 3$,所以本题中 $m>0$。
|
||||
- $m=1$,此时 $n=(11)_k$,即 $k=n-1\geq 2$,这保证了本题有解。
|
||||
|
||||
然后我们分别证明一般情况下的两个结论,以帮助解决本题。
|
||||
|
||||
**结论一:$m < \log_k n$**
|
||||
|
||||
注意到 $(1)$ 式右侧是一个首项为 $1$、公比为 $k$ 的等比数列,利用等比数列求和公式,我们可以得到:
|
||||
|
||||
$$
|
||||
n = \frac{1 - k^{m+1}}{1 - k}
|
||||
$$
|
||||
|
||||
对公式进行变换可得:
|
||||
|
||||
$$
|
||||
k^{m+1} = kn - n + 1 < kn
|
||||
$$
|
||||
|
||||
移项并化简可得:
|
||||
|
||||
$$
|
||||
m < \log_k n
|
||||
$$
|
||||
|
||||
这个结论帮助我们限制了 $m$ 的范围,本题中 $3 \leq n \leq 10^{18}$ 且 $k \geq 2$,所以 $m < \log_2 10^{18} < 60$。
|
||||
|
||||
**结论二:$k = \lfloor \sqrt[m]{n} \rfloor$**
|
||||
|
||||
依据 $(1)$ 式,可知:
|
||||
|
||||
$$
|
||||
n = k^0 + k^1 + k^2 + \dots + k^m > k^m \tag{2}
|
||||
$$
|
||||
|
||||
依据二项式定理可知:
|
||||
|
||||
$$
|
||||
(k+1)^m = \binom{0}k^0 + \binom{1}k^1 + \binom{2}k^2 + \dots + \binomk^m
|
||||
$$
|
||||
|
||||
因为当 $m>1$ 时,$\forall i \in [1,m-1], \dbinom{m}{i} > 1$,所以有:
|
||||
|
||||
$$
|
||||
\begin
|
||||
(k+1)^m &= \binom{0}k^0 + \binom{1}k^1 + \binom{2}k^2 + \dots + \binomk^m \\
|
||||
&> k^0 + k^1 + k^2 + \dots + k^m = n \tag{3}
|
||||
\end
|
||||
$$
|
||||
|
||||
结合 $(2)(3)$ 两式可知,当 $m>1$ 时,有 $k^m < n < (k+1)^m$。两边同时开方得:
|
||||
|
||||
$$
|
||||
k < \sqrt[m] < k+1
|
||||
$$
|
||||
|
||||
依据这个公式我们知道,$\sqrt[m]{n}$ 必然为一个小数,且 $k$ 为 $\sqrt[m]{n}$ 的整数部分,即 $k = \lfloor \sqrt[m]{n} \rfloor$。
|
||||
|
||||
这个结论帮助我们在 $n$ 和 $m$ 已知的情况下快速确定 $k$ 的值。
|
||||
|
||||
综合上述两个结论,依据结论一,我们知道 $m$ 的取值范围为 $[1,\log_k n)$,且 $m = 1$ 时必然有解。因为随着 $m$ 的增大,$k$ 不断减小,所以我们只需要从大到小检查每一个 $m$ 可能的取值,利用结论二快速算出对应的 $k$ 值,然后校验计算出的 $k$ 值是否有效即可。如果 $k$ 值有效,我们即可返回结果。
|
||||
|
||||
在实际代码中,我们首先算出 $m$ 取值的上界 $\textit{mMax}$,然后从上界开始向下枚举 $m$ 值,如果当前 $m$ 值对应的 $k$ 合法,那么我们即可返回当前的 $k$ 值。如果我们一直检查到 $m=2$ 都没能找到答案,那么此时即可直接返回 $m=1$ 对应的 $k$ 值:$n-1$。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
string smallestGoodBase(string n) {
|
||||
long nVal = stol(n);
|
||||
int mMax = floor(log(nVal) / log(2));
|
||||
for (int m = mMax; m > 1; m--) {
|
||||
int k = pow(nVal, 1.0 / m);
|
||||
long mul = 1, sum = 1;
|
||||
for (int i = 0; i < m; i++) {
|
||||
mul *= k;
|
||||
sum += mul;
|
||||
}
|
||||
if (sum == nVal) {
|
||||
return to_string(k);
|
||||
}
|
||||
}
|
||||
return to_string(nVal - 1);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public String smallestGoodBase(String n) {
|
||||
long nVal = Long.parseLong(n);
|
||||
int mMax = (int) Math.floor(Math.log(nVal) / Math.log(2));
|
||||
for (int m = mMax; m > 1; m--) {
|
||||
int k = (int) Math.pow(nVal, 1.0 / m);
|
||||
long mul = 1, sum = 1;
|
||||
for (int i = 0; i < m; i++) {
|
||||
mul *= k;
|
||||
sum += mul;
|
||||
}
|
||||
if (sum == nVal) {
|
||||
return Integer.toString(k);
|
||||
}
|
||||
}
|
||||
return Long.toString(nVal - 1);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C#]
|
||||
|
||||
```C#
|
||||
public class Solution {
|
||||
public string SmallestGoodBase(string n) {
|
||||
long nVal = long.Parse(n);
|
||||
int mMax = (int) Math.Floor(Math.Log(nVal) / Math.Log(2));
|
||||
for (int m = mMax; m > 1; m--) {
|
||||
int k = (int) Math.Pow(nVal, 1.0 / m);
|
||||
long mul = 1, sum = 1;
|
||||
for (int i = 0; i < m; i++) {
|
||||
mul *= k;
|
||||
sum += mul;
|
||||
}
|
||||
if (sum == nVal) {
|
||||
return k.ToString();
|
||||
}
|
||||
}
|
||||
return (nVal - 1).ToString();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var smallestGoodBase = function(n) {
|
||||
const nVal = parseInt(n);
|
||||
const mMax = Math.floor(Math.log(nVal) / Math.log(2));
|
||||
for (let m = mMax; m > 1; m--) {
|
||||
const k = BigInt(Math.floor(Math.pow(nVal, 1.0 / m)));
|
||||
if (k > 1) {
|
||||
let mul = BigInt(1), sum = BigInt(1);
|
||||
for (let i = 1; i <= m; i++) {
|
||||
mul *= k;
|
||||
sum += mul;
|
||||
}
|
||||
if (sum === BigInt(n)) {
|
||||
return k + '';
|
||||
}
|
||||
}
|
||||
}
|
||||
return (BigInt(n) - BigInt(1)) + '';
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
func smallestGoodBase(n string) string {
|
||||
nVal, _ := strconv.Atoi(n)
|
||||
mMax := bits.Len(uint(nVal)) - 1
|
||||
for m := mMax; m > 1; m-- {
|
||||
k := int(math.Pow(float64(nVal), 1/float64(m)))
|
||||
mul, sum := 1, 1
|
||||
for i := 0; i < m; i++ {
|
||||
mul *= k
|
||||
sum += mul
|
||||
}
|
||||
if sum == nVal {
|
||||
return strconv.Itoa(k)
|
||||
}
|
||||
}
|
||||
return strconv.Itoa(nVal - 1)
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
char* smallestGoodBase(char* n) {
|
||||
long nVal = atol(n);
|
||||
int mMax = floor(log(nVal) / log(2));
|
||||
char* ret = malloc(sizeof(char) * (mMax + 1));
|
||||
for (int m = mMax; m > 1; m--) {
|
||||
int k = pow(nVal, 1.0 / m);
|
||||
long mul = 1, sum = 1;
|
||||
for (int i = 0; i < m; i++) {
|
||||
mul *= k;
|
||||
sum += mul;
|
||||
}
|
||||
if (sum == nVal) {
|
||||
sprintf(ret, "%lld", k);
|
||||
return ret;
|
||||
}
|
||||
}
|
||||
sprintf(ret, "%lld", nVal - 1);
|
||||
return ret;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(\log^2 n)$。至多需要进行 $O(\log n)$ 次检查,每次检查的时间复杂度为 $O(\log n)$。
|
||||
|
||||
- 空间复杂度:$O(1)$。只需要常数的空间保存若干变量。
|
||||
|
||||
@ -0,0 +1,956 @@
|
||||
#### 前言
|
||||
|
||||
我们可以将本题抽象成如下的一个图论模型:
|
||||
|
||||
- 我们将地图中的每一个格子看成图中的一个节点;
|
||||
|
||||
- 我么将两个相邻(左右相邻或者上下相邻)的两个格子对应的节点之间连接一条无向边,边的权值为这两个格子的高度差的绝对值;
|
||||
|
||||
- 我们需要找到一条从左上角到右下角的**最短**路径,其中一条路径的长度定义为其经过的所有边权的**最大值**。
|
||||
|
||||
由于地图是二维的,我们需要给每个格子对应的节点赋予一个唯一的节点编号。如果地图的行数为 $m$,列数为 $n$,那么位置为 $(i, j)$ 的格子对应的编号为 $i \times n + j$,这样 $,mn$ 个格子的编号一一对应着 $[0, mn)$ 范围内的所有整数。当然,如果读者使用的语言支持对二元组进行哈希计算、作为下标访问等,则不需要这一步操作。
|
||||
|
||||
本篇题解中会介绍三种不同的解决方法。
|
||||
|
||||
#### 方法一:二分查找
|
||||
|
||||
**思路与算法**
|
||||
|
||||
我们可以将这个问题转化成一个「判定性」问题,即:
|
||||
|
||||
> 是否存在一条从左上角到右下角的路径,其经过的所有边权的最大值不超过 $x$?
|
||||
|
||||
这个判定性问题解决起来并不复杂,我们只要从左上角开始进行深度优先搜索或者广度优先搜索,在搜索的过程中只允许经过边权不超过 $x$ 的边,搜索结束后判断是否能到达右下角即可。
|
||||
|
||||
随着 $x$ 的增大,原先可以经过的边仍然会被保留,因此如果当 $x=x_0$ 时,我们可以从左上角到达右下角,那么当 $x > x_0$ 时同样也可以可行的。因此我们可以使用二分查找的方法,找出满足要求的最小的那个 $x$ 值,记为 $x_\textit{ans}$,那么:
|
||||
|
||||
- 当 $x < x_\textit{ans}$,我们无法从左上角到达右下角;
|
||||
|
||||
- 当 $x \geq x_\textit{ans}$,我们可以从左上角到达右下角。
|
||||
|
||||
由于格子的高度范围为 $[1, 10^6]$,因此我们可以 $[0, 10^6-1]$ 的范围内对 $x$ 进行二分查找。在每一步查找的过程中,我们使用进行深度优先搜索或者广度优先搜索判断是否可以从左上角到达右下角,并根据判定结果更新二分查找的左边界或右边界即可。
|
||||
|
||||
**代码**
|
||||
|
||||
下面的代码中使用的是广度优先搜索。
|
||||
|
||||
* [sol1-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
|
||||
|
||||
public:
|
||||
int minimumEffortPath(vector<vector<int>>& heights) {
|
||||
int m = heights.size();
|
||||
int n = heights[0].size();
|
||||
int left = 0, right = 999999, ans = 0;
|
||||
while (left <= right) {
|
||||
int mid = (left + right) / 2;
|
||||
queue<pair<int, int>> q;
|
||||
q.emplace(0, 0);
|
||||
vector<int> seen(m * n);
|
||||
seen[0] = 1;
|
||||
while (!q.empty()) {
|
||||
auto [x, y] = q.front();
|
||||
q.pop();
|
||||
for (int i = 0; i < 4; ++i) {
|
||||
int nx = x + dirs[i][0];
|
||||
int ny = y + dirs[i][1];
|
||||
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && abs(heights[x][y] - heights[nx][ny]) <= mid) {
|
||||
q.emplace(nx, ny);
|
||||
seen[nx * n + ny] = 1;
|
||||
}
|
||||
}
|
||||
}
|
||||
if (seen[m * n - 1]) {
|
||||
ans = mid;
|
||||
right = mid - 1;
|
||||
}
|
||||
else {
|
||||
left = mid + 1;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
|
||||
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
int m = heights.length;
|
||||
int n = heights[0].length;
|
||||
int left = 0, right = 999999, ans = 0;
|
||||
while (left <= right) {
|
||||
int mid = (left + right) / 2;
|
||||
Queue<int[]> queue = new LinkedList<int[]>();
|
||||
queue.offer(new int[]{0, 0});
|
||||
boolean[] seen = new boolean[m * n];
|
||||
seen[0] = true;
|
||||
while (!queue.isEmpty()) {
|
||||
int[] cell = queue.poll();
|
||||
int x = cell[0], y = cell[1];
|
||||
for (int i = 0; i < 4; ++i) {
|
||||
int nx = x + dirs[i][0];
|
||||
int ny = y + dirs[i][1];
|
||||
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && Math.abs(heights[x][y] - heights[nx][ny]) <= mid) {
|
||||
queue.offer(new int[]{nx, ny});
|
||||
seen[nx * n + ny] = true;
|
||||
}
|
||||
}
|
||||
}
|
||||
if (seen[m * n - 1]) {
|
||||
ans = mid;
|
||||
right = mid - 1;
|
||||
} else {
|
||||
left = mid + 1;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def minimumEffortPath(self, heights: List[List[int]]) -> int:
|
||||
m, n = len(heights), len(heights[0])
|
||||
left, right, ans = 0, 10**6 - 1, 0
|
||||
|
||||
while left <= right:
|
||||
mid = (left + right) // 2
|
||||
q = collections.deque([(0, 0)])
|
||||
seen = {(0, 0)}
|
||||
|
||||
while q:
|
||||
x, y = q.popleft()
|
||||
for nx, ny in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
|
||||
if 0 <= nx < m and 0 <= ny < n and (nx, ny) not in seen and abs(heights[x][y] - heights[nx][ny]) <= mid:
|
||||
q.append((nx, ny))
|
||||
seen.add((nx, ny))
|
||||
|
||||
if (m - 1, n - 1) in seen:
|
||||
ans = mid
|
||||
right = mid - 1
|
||||
else:
|
||||
left = mid + 1
|
||||
|
||||
return ans
|
||||
```
|
||||
|
||||
* [sol1-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var minimumEffortPath = function(heights) {
|
||||
const dirs = [[-1, 0], [1, 0], [0, -1], [0, 1]];
|
||||
|
||||
const m = heights.length, n = heights[0].length;
|
||||
let left = 0, right = 999999, ans = 0;
|
||||
while (left <= right) {
|
||||
const mid = Math.floor((left + right) / 2);
|
||||
const queue = [[0, 0]];
|
||||
const seen = new Array(m * n).fill(0);
|
||||
seen[0] = 1;
|
||||
while (queue.length) {
|
||||
const [x, y] = queue.shift();
|
||||
for (let i = 0; i < 4; i++) {
|
||||
const nx = x + dirs[i][0];
|
||||
const ny = y + dirs[i][1];
|
||||
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && Math.abs(heights[x][y] - heights[nx][ny]) <= mid) {
|
||||
queue.push([nx, ny]);
|
||||
seen[nx * n + ny] = 1;
|
||||
}
|
||||
}
|
||||
}
|
||||
if (seen[m * n - 1]) {
|
||||
ans = mid;
|
||||
right = mid - 1;
|
||||
} else {
|
||||
left = mid + 1;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
};
|
||||
```
|
||||
|
||||
* [sol1-Golang]
|
||||
|
||||
```go
|
||||
type pair struct{ x, y int }
|
||||
var dirs = []pair{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
|
||||
|
||||
func minimumEffortPath(heights [][]int) int {
|
||||
n, m := len(heights), len(heights[0])
|
||||
return sort.Search(1e6, func(maxHeightDiff int) bool {
|
||||
vis := make([][]bool, n)
|
||||
for i := range vis {
|
||||
vis[i] = make([]bool, m)
|
||||
}
|
||||
vis[0][0] = true
|
||||
queue := []pair{{}}
|
||||
for len(queue) > 0 {
|
||||
p := queue[0]
|
||||
queue = queue[1:]
|
||||
if p.x == n-1 && p.y == m-1 {
|
||||
return true
|
||||
}
|
||||
for _, d := range dirs {
|
||||
x, y := p.x+d.x, p.y+d.y
|
||||
if 0 <= x && x < n && 0 <= y && y < m && !vis[x][y] && abs(heights[x][y]-heights[p.x][p.y]) <= maxHeightDiff {
|
||||
vis[x][y] = true
|
||||
queue = append(queue, pair{x, y})
|
||||
}
|
||||
}
|
||||
}
|
||||
return false
|
||||
})
|
||||
}
|
||||
|
||||
func abs(x int) int {
|
||||
if x < 0 {
|
||||
return -x
|
||||
}
|
||||
return x
|
||||
}
|
||||
```
|
||||
|
||||
* [sol1-C]
|
||||
|
||||
```C
|
||||
int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
|
||||
|
||||
int minimumEffortPath(int** heights, int heightsSize, int* heightsColSize) {
|
||||
int m = heightsSize;
|
||||
int n = heightsColSize[0];
|
||||
int left = 0, right = 999999, ans = 0;
|
||||
while (left <= right) {
|
||||
int mid = (left + right) / 2;
|
||||
int q[n * m][2];
|
||||
int qleft = 0, qright = 0;
|
||||
q[qright][0] = 0, q[qright++][1] = 0;
|
||||
int seen[m * n];
|
||||
memset(seen, 0, sizeof(seen));
|
||||
seen[0] = 1;
|
||||
while (qleft < qright) {
|
||||
int x = q[qleft][0], y = q[qleft++][1];
|
||||
for (int i = 0; i < 4; ++i) {
|
||||
int nx = x + dirs[i][0];
|
||||
int ny = y + dirs[i][1];
|
||||
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && abs(heights[x][y] - heights[nx][ny]) <= mid) {
|
||||
q[qright][0] = nx, q[qright++][1] = ny;
|
||||
seen[nx * n + ny] = 1;
|
||||
}
|
||||
}
|
||||
}
|
||||
if (seen[m * n - 1]) {
|
||||
ans = mid;
|
||||
right = mid - 1;
|
||||
} else {
|
||||
left = mid + 1;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(mn \log C)$,其中 $m$ 和 $n$ 分别是地图的行数和列数,$C$ 是格子的最大高度,在本题中 $C$ 不超过 $10^6$。我们需要进行 $O(\log C)$ 次二分查找,每一步查找的过程中需要使用广度优先搜索,在 $O(mn)$ 的时间判断是否可以从左上角到达右下角,因此总时间复杂度为 $O(mn \log C)$。
|
||||
|
||||
- 空间复杂度:$O(mn)$,即为广度优先搜索中使用的队列需要的空间。
|
||||
|
||||
#### 方法二:并查集
|
||||
|
||||
**思路与算法**
|
||||
|
||||
我们将这 $mn$ 个节点放入并查集中,实时维护它们的连通性。
|
||||
|
||||
由于我们需要找到从左上角到右下角的最短路径,因此我们可以将图中的所有边按照权值从小到大进行排序,并依次加入并查集中。当我们加入一条权值为 $x$ 的边之后,如果左上角和右下角从非连通状态变为连通状态,那么 $x$ 即为答案。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol2-C++]
|
||||
|
||||
```C++
|
||||
// 并查集模板
|
||||
class UnionFind {
|
||||
public:
|
||||
vector<int> parent;
|
||||
vector<int> size;
|
||||
int n;
|
||||
// 当前连通分量数目
|
||||
int setCount;
|
||||
|
||||
public:
|
||||
UnionFind(int _n): n(_n), setCount(_n), parent(_n), size(_n, 1) {
|
||||
iota(parent.begin(), parent.end(), 0);
|
||||
}
|
||||
|
||||
int findset(int x) {
|
||||
return parent[x] == x ? x : parent[x] = findset(parent[x]);
|
||||
}
|
||||
|
||||
bool unite(int x, int y) {
|
||||
x = findset(x);
|
||||
y = findset(y);
|
||||
if (x == y) {
|
||||
return false;
|
||||
}
|
||||
if (size[x] < size[y]) {
|
||||
swap(x, y);
|
||||
}
|
||||
parent[y] = x;
|
||||
size[x] += size[y];
|
||||
--setCount;
|
||||
return true;
|
||||
}
|
||||
|
||||
bool connected(int x, int y) {
|
||||
x = findset(x);
|
||||
y = findset(y);
|
||||
return x == y;
|
||||
}
|
||||
};
|
||||
|
||||
class Solution {
|
||||
public:
|
||||
int minimumEffortPath(vector<vector<int>>& heights) {
|
||||
int m = heights.size();
|
||||
int n = heights[0].size();
|
||||
vector<tuple<int, int, int>> edges;
|
||||
for (int i = 0; i < m; ++i) {
|
||||
for (int j = 0; j < n; ++j) {
|
||||
int id = i * n + j;
|
||||
if (i > 0) {
|
||||
edges.emplace_back(id - n, id, abs(heights[i][j] - heights[i - 1][j]));
|
||||
}
|
||||
if (j > 0) {
|
||||
edges.emplace_back(id - 1, id, abs(heights[i][j] - heights[i][j - 1]));
|
||||
}
|
||||
}
|
||||
}
|
||||
sort(edges.begin(), edges.end(), [](const auto& e1, const auto& e2) {
|
||||
auto&& [x1, y1, v1] = e1;
|
||||
auto&& [x2, y2, v2] = e2;
|
||||
return v1 < v2;
|
||||
});
|
||||
|
||||
UnionFind uf(m * n);
|
||||
int ans = 0;
|
||||
for (const auto [x, y, v]: edges) {
|
||||
uf.unite(x, y);
|
||||
if (uf.connected(0, m * n - 1)) {
|
||||
ans = v;
|
||||
break;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol2-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
int m = heights.length;
|
||||
int n = heights[0].length;
|
||||
List<int[]> edges = new ArrayList<int[]>();
|
||||
for (int i = 0; i < m; ++i) {
|
||||
for (int j = 0; j < n; ++j) {
|
||||
int id = i * n + j;
|
||||
if (i > 0) {
|
||||
edges.add(new int[]{id - n, id, Math.abs(heights[i][j] - heights[i - 1][j])});
|
||||
}
|
||||
if (j > 0) {
|
||||
edges.add(new int[]{id - 1, id, Math.abs(heights[i][j] - heights[i][j - 1])});
|
||||
}
|
||||
}
|
||||
}
|
||||
Collections.sort(edges, new Comparator<int[]>() {
|
||||
public int compare(int[] edge1, int[] edge2) {
|
||||
return edge1[2] - edge2[2];
|
||||
}
|
||||
});
|
||||
|
||||
UnionFind uf = new UnionFind(m * n);
|
||||
int ans = 0;
|
||||
for (int[] edge : edges) {
|
||||
int x = edge[0], y = edge[1], v = edge[2];
|
||||
uf.unite(x, y);
|
||||
if (uf.connected(0, m * n - 1)) {
|
||||
ans = v;
|
||||
break;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
|
||||
// 并查集模板
|
||||
class UnionFind {
|
||||
int[] parent;
|
||||
int[] size;
|
||||
int n;
|
||||
// 当前连通分量数目
|
||||
int setCount;
|
||||
|
||||
public UnionFind(int n) {
|
||||
this.n = n;
|
||||
this.setCount = n;
|
||||
this.parent = new int[n];
|
||||
this.size = new int[n];
|
||||
Arrays.fill(size, 1);
|
||||
for (int i = 0; i < n; ++i) {
|
||||
parent[i] = i;
|
||||
}
|
||||
}
|
||||
|
||||
public int findset(int x) {
|
||||
return parent[x] == x ? x : (parent[x] = findset(parent[x]));
|
||||
}
|
||||
|
||||
public boolean unite(int x, int y) {
|
||||
x = findset(x);
|
||||
y = findset(y);
|
||||
if (x == y) {
|
||||
return false;
|
||||
}
|
||||
if (size[x] < size[y]) {
|
||||
int temp = x;
|
||||
x = y;
|
||||
y = temp;
|
||||
}
|
||||
parent[y] = x;
|
||||
size[x] += size[y];
|
||||
--setCount;
|
||||
return true;
|
||||
}
|
||||
|
||||
public boolean connected(int x, int y) {
|
||||
x = findset(x);
|
||||
y = findset(y);
|
||||
return x == y;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Python3]
|
||||
|
||||
```Python
|
||||
# 并查集模板
|
||||
class UnionFind:
|
||||
def __init__(self, n: int):
|
||||
self.parent = list(range(n))
|
||||
self.size = [1] * n
|
||||
self.n = n
|
||||
# 当前连通分量数目
|
||||
self.setCount = n
|
||||
|
||||
def findset(self, x: int) -> int:
|
||||
if self.parent[x] == x:
|
||||
return x
|
||||
self.parent[x] = self.findset(self.parent[x])
|
||||
return self.parent[x]
|
||||
|
||||
def unite(self, x: int, y: int) -> bool:
|
||||
x, y = self.findset(x), self.findset(y)
|
||||
if x == y:
|
||||
return False
|
||||
if self.size[x] < self.size[y]:
|
||||
x, y = y, x
|
||||
self.parent[y] = x
|
||||
self.size[x] += self.size[y]
|
||||
self.setCount -= 1
|
||||
return True
|
||||
|
||||
def connected(self, x: int, y: int) -> bool:
|
||||
x, y = self.findset(x), self.findset(y)
|
||||
return x == y
|
||||
|
||||
class Solution:
|
||||
def minimumEffortPath(self, heights: List[List[int]]) -> int:
|
||||
m, n = len(heights), len(heights[0])
|
||||
edges = list()
|
||||
for i in range(m):
|
||||
for j in range(n):
|
||||
iden = i * n + j
|
||||
if i > 0:
|
||||
edges.append((iden - n, iden, abs(heights[i][j] - heights[i - 1][j])))
|
||||
if j > 0:
|
||||
edges.append((iden - 1, iden, abs(heights[i][j] - heights[i][j - 1])))
|
||||
|
||||
edges.sort(key=lambda e: e[2])
|
||||
|
||||
uf = UnionFind(m * n)
|
||||
ans = 0
|
||||
for x, y, v in edges:
|
||||
uf.unite(x, y)
|
||||
if uf.connected(0, m * n - 1):
|
||||
ans = v
|
||||
break
|
||||
|
||||
return ans
|
||||
```
|
||||
|
||||
* [sol2-JavaScript]
|
||||
|
||||
```JavaScript
|
||||
var minimumEffortPath = function(heights) {
|
||||
const m = heights.length;
|
||||
const n = heights[0].length;
|
||||
const edges = [];
|
||||
for (let i = 0; i < m; ++i) {
|
||||
for (let j = 0; j < n; ++j) {
|
||||
const id = i * n + j;
|
||||
if (i > 0) {
|
||||
edges.push([id - n, id, Math.abs(heights[i][j] - heights[i - 1][j])]);
|
||||
}
|
||||
if (j > 0) {
|
||||
edges.push([id - 1, id, Math.abs(heights[i][j] - heights[i][j - 1])]);
|
||||
}
|
||||
}
|
||||
}
|
||||
edges.sort((a, b) => a[2] - b[2]);
|
||||
|
||||
const uf = new UnionFind(m * n);
|
||||
let ans = 0;
|
||||
for (const edge of edges) {
|
||||
const x = edge[0], y = edge[1], v = edge[2];
|
||||
uf.unite(x, y);
|
||||
if (uf.connected(0, m * n - 1)) {
|
||||
ans = v;
|
||||
break;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
};
|
||||
|
||||
// 并查集模板
|
||||
class UnionFind {
|
||||
constructor (n) {
|
||||
this.parent = new Array(n).fill(0).map((element, index) => index);
|
||||
this.size = new Array(n).fill(1);
|
||||
// 当前连通分量数目
|
||||
this.setCount = n;
|
||||
}
|
||||
|
||||
findset (x) {
|
||||
if (this.parent[x] === x) {
|
||||
return x;
|
||||
}
|
||||
this.parent[x] = this.findset(this.parent[x]);
|
||||
return this.parent[x];
|
||||
}
|
||||
|
||||
unite (a, b) {
|
||||
let x = this.findset(a), y = this.findset(b);
|
||||
if (x === y) {
|
||||
return false;
|
||||
}
|
||||
if (this.size[x] < this.size[y]) {
|
||||
[x, y] = [y, x];
|
||||
}
|
||||
this.parent[y] = x;
|
||||
this.size[x] += this.size[y];
|
||||
this.setCount -= 1;
|
||||
return true;
|
||||
}
|
||||
|
||||
connected (a, b) {
|
||||
const x = this.findset(a), y = this.findset(b);
|
||||
return x === y;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-Golang]
|
||||
|
||||
```go
|
||||
type unionFind struct {
|
||||
parent, size []int
|
||||
}
|
||||
|
||||
func newUnionFind(n int) *unionFind {
|
||||
parent := make([]int, n)
|
||||
size := make([]int, n)
|
||||
for i := range parent {
|
||||
parent[i] = i
|
||||
size[i] = 1
|
||||
}
|
||||
return &unionFind{parent, size}
|
||||
}
|
||||
|
||||
func (uf *unionFind) find(x int) int {
|
||||
if uf.parent[x] != x {
|
||||
uf.parent[x] = uf.find(uf.parent[x])
|
||||
}
|
||||
return uf.parent[x]
|
||||
}
|
||||
|
||||
func (uf *unionFind) union(x, y int) {
|
||||
fx, fy := uf.find(x), uf.find(y)
|
||||
if fx == fy {
|
||||
return
|
||||
}
|
||||
if uf.size[fx] < uf.size[fy] {
|
||||
fx, fy = fy, fx
|
||||
}
|
||||
uf.size[fx] += uf.size[fy]
|
||||
uf.parent[fy] = fx
|
||||
}
|
||||
|
||||
func (uf *unionFind) inSameSet(x, y int) bool {
|
||||
return uf.find(x) == uf.find(y)
|
||||
}
|
||||
|
||||
type edge struct {
|
||||
v, w, diff int
|
||||
}
|
||||
|
||||
func minimumEffortPath(heights [][]int) int {
|
||||
n, m := len(heights), len(heights[0])
|
||||
edges := []edge{}
|
||||
for i, row := range heights {
|
||||
for j, h := range row {
|
||||
id := i*m + j
|
||||
if i > 0 {
|
||||
edges = append(edges, edge{id - m, id, abs(h - heights[i-1][j])})
|
||||
}
|
||||
if j > 0 {
|
||||
edges = append(edges, edge{id - 1, id, abs(h - heights[i][j-1])})
|
||||
}
|
||||
}
|
||||
}
|
||||
sort.Slice(edges, func(i, j int) bool { return edges[i].diff < edges[j].diff })
|
||||
|
||||
uf := newUnionFind(n * m)
|
||||
for _, e := range edges {
|
||||
uf.union(e.v, e.w)
|
||||
if uf.inSameSet(0, n*m-1) {
|
||||
return e.diff
|
||||
}
|
||||
}
|
||||
return 0
|
||||
}
|
||||
|
||||
func abs(x int) int {
|
||||
if x < 0 {
|
||||
return -x
|
||||
}
|
||||
return x
|
||||
}
|
||||
```
|
||||
|
||||
* [sol2-C]
|
||||
|
||||
```C
|
||||
void swap(int* a, int* b) {
|
||||
int tmp = *a;
|
||||
*a = *b, *b = tmp;
|
||||
}
|
||||
|
||||
struct DisjointSetUnion {
|
||||
int *f, *size;
|
||||
int n, setCount;
|
||||
};
|
||||
|
||||
void initDSU(struct DisjointSetUnion* obj, int n) {
|
||||
obj->f = malloc(sizeof(int) * n);
|
||||
obj->size = malloc(sizeof(int) * n);
|
||||
obj->n = n;
|
||||
obj->setCount = n;
|
||||
for (int i = 0; i < n; i++) {
|
||||
obj->f[i] = i;
|
||||
obj->size[i] = 1;
|
||||
}
|
||||
}
|
||||
|
||||
int find(struct DisjointSetUnion* obj, int x) {
|
||||
return obj->f[x] == x ? x : (obj->f[x] = find(obj, obj->f[x]));
|
||||
}
|
||||
|
||||
int unionSet(struct DisjointSetUnion* obj, int x, int y) {
|
||||
int fx = find(obj, x), fy = find(obj, y);
|
||||
if (fx == fy) {
|
||||
return false;
|
||||
}
|
||||
if (obj->size[fx] < obj->size[fy]) {
|
||||
swap(&fx, &fy);
|
||||
}
|
||||
obj->size[fx] += obj->size[fy];
|
||||
obj->f[fy] = fx;
|
||||
obj->setCount--;
|
||||
return true;
|
||||
}
|
||||
|
||||
int connected(struct DisjointSetUnion* obj, int x, int y) {
|
||||
return find(obj, x) == find(obj, y);
|
||||
}
|
||||
|
||||
struct Tuple {
|
||||
int x, y, z
|
||||
};
|
||||
|
||||
int cmp(const struct Tuple* a, const struct Tuple* b) {
|
||||
return a->z - b->z;
|
||||
}
|
||||
|
||||
int minimumEffortPath(int** heights, int heightsSize, int* heightsColSize) {
|
||||
int m = heightsSize;
|
||||
int n = heightsColSize[0];
|
||||
struct Tuple edges[n * m * 2];
|
||||
int edgesSize = 0;
|
||||
for (int i = 0; i < m; ++i) {
|
||||
for (int j = 0; j < n; ++j) {
|
||||
int id = i * n + j;
|
||||
if (i > 0) {
|
||||
edges[edgesSize].x = id - n;
|
||||
edges[edgesSize].y = id;
|
||||
edges[edgesSize++].z = fabs(heights[i][j] - heights[i - 1][j]);
|
||||
}
|
||||
if (j > 0) {
|
||||
edges[edgesSize].x = id - 1;
|
||||
edges[edgesSize].y = id;
|
||||
edges[edgesSize++].z = fabs(heights[i][j] - heights[i][j - 1]);
|
||||
}
|
||||
}
|
||||
}
|
||||
qsort(edges, edgesSize, sizeof(struct Tuple), cmp);
|
||||
|
||||
struct DisjointSetUnion* uf = malloc(sizeof(struct DisjointSetUnion));
|
||||
initDSU(uf, m * n);
|
||||
int ans = 0;
|
||||
for (int i = 0; i < edgesSize; i++) {
|
||||
unionSet(uf, edges[i].x, edges[i].y);
|
||||
if (connected(uf, 0, m * n - 1)) {
|
||||
ans = edges[i].z;
|
||||
break;
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(mn \log(mn))$,其中 $m$ 和 $n$ 分别是地图的行数和列数。图中的边数为 $O(mn)$,因此排序的时间复杂度为 $O(mn \log (mn))$。并查集的时间复杂度为 $O(mn \cdot \alpha(mn))$,其中 $\alpha$ 为阿克曼函数的反函数。由于后者在渐进意义下小于前者,因此总时间复杂度为 $O(mn \log(mn))$。
|
||||
|
||||
- 空间复杂度:$O(mn)$,即为存储所有边以及并查集需要的空间。
|
||||
|
||||
#### 方法三:最短路
|
||||
|
||||
**思路与算法**
|
||||
|
||||
「最短路径」使得我们很容易想到求解最短路径的 $\texttt{Dijkstra}$ 算法,然而本题中对于「最短路径」的定义不是其经过的所有边权的和,而是其经过的所有边权的**最大值**,那么我们还可以用 $\texttt{Dijkstra}$ 算法进行求解吗?
|
||||
|
||||
答案是可以的。$\texttt{Dijkstra}$ 算法本质上是一种启发式搜索算法,它是 $\texttt{A*}$ 算法在启发函数 $h \equiv 0$ 时的特殊情况。读者可以参考 [A* search algorithm](https://en.wikipedia.org/wiki/A*_search_algorithm),[Consistent heuristic](https://en.wikipedia.org/wiki/Consistent_heuristic),[Admissible heuristic](https://en.wikipedia.org/wiki/Admissible_heuristic) 深入了解 $\texttt{Dijkstra}$ 算法的本质。
|
||||
|
||||
下面给出 $\texttt{Dijkstra}$ 算法的可行性证明,需要读者对 $\texttt{A*}$ 算法以及其可行性条件有一定的掌握。
|
||||
|
||||
**证明**
|
||||
|
||||
定义加法运算 $a \oplus b = \max (a,b)$,显然 $\oplus$ 满足交换律和结合律。那么如果一条路径上的边权分别为 $e_0, e_1, \cdots, e_k$,那么 $e_0 \oplus e_1 \oplus \cdots \oplus e_k$ 即为这条路径的长度。
|
||||
|
||||
在 $\texttt{Dijkstra}$ 算法中 $h \equiv 0$,对于图中任意的无向边 $x \leftrightarrow y$,由于 $e_{x, y} \geq 0$,那么 $h(x)=0\leq e_{x,y} \oplus h(y)$ 恒成立,其中 $e_{x, y}$ 表示边权。因此启发函数 $h$ 和加法运算 $\oplus$ 满足三角不等式,是 consistent heuristic 的,可以使用 $\texttt{Dijkstra}$ 算法求出最短路径。
|
||||
|
||||
**代码**
|
||||
|
||||
* [sol3-C++]
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
|
||||
|
||||
public:
|
||||
int minimumEffortPath(vector<vector<int>>& heights) {
|
||||
int m = heights.size();
|
||||
int n = heights[0].size();
|
||||
|
||||
auto tupleCmp = [](const auto& e1, const auto& e2) {
|
||||
auto&& [x1, y1, d1] = e1;
|
||||
auto&& [x2, y2, d2] = e2;
|
||||
return d1 > d2;
|
||||
};
|
||||
priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, decltype(tupleCmp)> q(tupleCmp);
|
||||
q.emplace(0, 0, 0);
|
||||
|
||||
vector<int> dist(m * n, INT_MAX);
|
||||
dist[0] = 0;
|
||||
vector<int> seen(m * n);
|
||||
|
||||
while (!q.empty()) {
|
||||
auto [x, y, d] = q.top();
|
||||
q.pop();
|
||||
int id = x * n + y;
|
||||
if (seen[id]) {
|
||||
continue;
|
||||
}
|
||||
if (x == m - 1 && y == n - 1) {
|
||||
break;
|
||||
}
|
||||
seen[id] = 1;
|
||||
for (int i = 0; i < 4; ++i) {
|
||||
int nx = x + dirs[i][0];
|
||||
int ny = y + dirs[i][1];
|
||||
if (nx >= 0 && nx < m && ny >= 0 && ny < n && max(d, abs(heights[x][y] - heights[nx][ny])) < dist[nx * n + ny]) {
|
||||
dist[nx * n + ny] = max(d, abs(heights[x][y] - heights[nx][ny]));
|
||||
q.emplace(nx, ny, dist[nx * n + ny]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dist[m * n - 1];
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* [sol3-Java]
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
|
||||
|
||||
public int minimumEffortPath(int[][] heights) {
|
||||
int m = heights.length;
|
||||
int n = heights[0].length;
|
||||
PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
|
||||
public int compare(int[] edge1, int[] edge2) {
|
||||
return edge1[2] - edge2[2];
|
||||
}
|
||||
});
|
||||
pq.offer(new int[]{0, 0, 0});
|
||||
|
||||
int[] dist = new int[m * n];
|
||||
Arrays.fill(dist, Integer.MAX_VALUE);
|
||||
dist[0] = 0;
|
||||
boolean[] seen = new boolean[m * n];
|
||||
|
||||
while (!pq.isEmpty()) {
|
||||
int[] edge = pq.poll();
|
||||
int x = edge[0], y = edge[1], d = edge[2];
|
||||
int id = x * n + y;
|
||||
if (seen[id]) {
|
||||
continue;
|
||||
}
|
||||
if (x == m - 1 && y == n - 1) {
|
||||
break;
|
||||
}
|
||||
seen[id] = true;
|
||||
for (int i = 0; i < 4; ++i) {
|
||||
int nx = x + dirs[i][0];
|
||||
int ny = y + dirs[i][1];
|
||||
if (nx >= 0 && nx < m && ny >= 0 && ny < n && Math.max(d, Math.abs(heights[x][y] - heights[nx][ny])) < dist[nx * n + ny]) {
|
||||
dist[nx * n + ny] = Math.max(d, Math.abs(heights[x][y] - heights[nx][ny]));
|
||||
pq.offer(new int[]{nx, ny, dist[nx * n + ny]});
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dist[m * n - 1];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* [sol3-Python3]
|
||||
|
||||
```Python
|
||||
class Solution:
|
||||
def minimumEffortPath(self, heights: List[List[int]]) -> int:
|
||||
m, n = len(heights), len(heights[0])
|
||||
q = [(0, 0, 0)]
|
||||
dist = [0] + [float("inf")] * (m * n - 1)
|
||||
seen = set()
|
||||
|
||||
while q:
|
||||
d, x, y = heapq.heappop(q)
|
||||
iden = x * n + y
|
||||
if iden in seen:
|
||||
continue
|
||||
if (x, y) == (m - 1, n - 1):
|
||||
break
|
||||
|
||||
seen.add(iden)
|
||||
for nx, ny in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
|
||||
if 0 <= nx < m and 0 <= ny < n and max(d, abs(heights[x][y] - heights[nx][ny])) <= dist[nx * n + ny]:
|
||||
dist[nx * n + ny] = max(d, abs(heights[x][y] - heights[nx][ny]))
|
||||
heapq.heappush(q, (dist[nx * n + ny], nx, ny))
|
||||
|
||||
return dist[m * n - 1]
|
||||
```
|
||||
|
||||
* [sol3-Golang]
|
||||
|
||||
```go
|
||||
type point struct{ x, y, maxDiff int }
|
||||
type hp []point
|
||||
func (h hp) Len() int { return len(h) }
|
||||
func (h hp) Less(i, j int) bool { return h[i].maxDiff < h[j].maxDiff }
|
||||
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
|
||||
func (h *hp) Push(v interface{}) { *h = append(*h, v.(point)) }
|
||||
func (h *hp) Pop() (v interface{}) { a := *h; *h, v = a[:len(a)-1], a[len(a)-1]; return }
|
||||
|
||||
type pair struct{ x, y int }
|
||||
var dir4 = []pair{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
|
||||
|
||||
func minimumEffortPath(heights [][]int) int {
|
||||
n, m := len(heights), len(heights[0])
|
||||
maxDiff := make([][]int, n)
|
||||
for i := range maxDiff {
|
||||
maxDiff[i] = make([]int, m)
|
||||
for j := range maxDiff[i] {
|
||||
maxDiff[i][j] = math.MaxInt64
|
||||
}
|
||||
}
|
||||
maxDiff[0][0] = 0
|
||||
h := &hp{{}}
|
||||
for {
|
||||
p := heap.Pop(h).(point)
|
||||
if p.x == n-1 && p.y == m-1 {
|
||||
return p.maxDiff
|
||||
}
|
||||
if maxDiff[p.x][p.y] < p.maxDiff {
|
||||
continue
|
||||
}
|
||||
for _, d := range dir4 {
|
||||
if x, y := p.x+d.x, p.y+d.y; 0 <= x && x < n && 0 <= y && y < m {
|
||||
if diff := max(p.maxDiff, abs(heights[x][y]-heights[p.x][p.y])); diff < maxDiff[x][y] {
|
||||
maxDiff[x][y] = diff
|
||||
heap.Push(h, point{x, y, diff})
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
|
||||
func abs(x int) int {
|
||||
if x < 0 {
|
||||
return -x
|
||||
}
|
||||
return x
|
||||
}
|
||||
```
|
||||
|
||||
**复杂度分析**
|
||||
|
||||
- 时间复杂度:$O(mn \log(mn))$,其中 $m$ 和 $n$ 分别是地图的行数和列数。对于节点数为 $n_0$,边数为 $m_0$ 的图,使用优先队列优化的 $\texttt{Dijkstra}$ 算法的时间复杂度为 $O(m_0 \log m_0)$。由于图中的边数为 $O(mn)$,带入即可得到时间复杂度 $O(mn \log(mn))$。
|
||||
|
||||
- 空间复杂度:$O(mn)$,即为 $\texttt{Dijkstra}$ 算法需要使用的空间。
|
||||
|
||||
@ -0,0 +1,46 @@
|
||||
class Solution {
|
||||
// List<List<Integer>> result = new ArrayList<>();
|
||||
//
|
||||
// public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
|
||||
// path(graph, 0, new ArrayList<>());
|
||||
// return result;
|
||||
// }
|
||||
//
|
||||
// public void path(int[][] graph, int index, List<Integer> list) {
|
||||
// list.add(index);
|
||||
// if (index == graph.length) {
|
||||
// result.add(new ArrayList<>(list));
|
||||
// list.remove(list.size() - 1);
|
||||
// return;
|
||||
// }
|
||||
// for (int i = 0; i < graph[index].length; i++) {
|
||||
// path(graph, graph[index][i], list);
|
||||
// }
|
||||
// list.remove(list.size() - 1);
|
||||
// }
|
||||
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
|
||||
return solve(graph, 0);
|
||||
}
|
||||
|
||||
public List<List<Integer>> solve(int[][] graph, int node) {
|
||||
int N = graph.length;
|
||||
List<List<Integer>> ans = new ArrayList();
|
||||
if (node == N - 1) {
|
||||
List<Integer> path = new ArrayList();
|
||||
path.add(N-1);
|
||||
ans.add(path);
|
||||
return ans;
|
||||
}
|
||||
|
||||
for (int nei: graph[node]) {
|
||||
for (List<Integer> path: solve(graph, nei)) {
|
||||
path.add(0, node);
|
||||
ans.add(path);
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
|
||||
//runtime:4 ms
|
||||
//memory:40.4 MB
|
||||
@ -0,0 +1,12 @@
|
||||
class Solution {
|
||||
public int[] buildArray(int[] nums) {
|
||||
int size = nums.length;
|
||||
int[] arr = new int[size];
|
||||
for (int i = 0; i < size; i++) {
|
||||
arr[i] = nums[nums[i]];
|
||||
}
|
||||
return arr;
|
||||
}
|
||||
}
|
||||
//runtime:1 ms
|
||||
//memory:39.2 MB
|
||||
@ -0,0 +1,17 @@
|
||||
class Solution {
|
||||
public boolean areOccurrencesEqual(String s) {
|
||||
int[] arr = new int[26];
|
||||
for (char ch : s.toCharArray()) {
|
||||
arr[ch - 'a']++;
|
||||
}
|
||||
int num = arr[s.charAt(0) - 'a'];
|
||||
for (int j : arr) {
|
||||
if (j > 0 && j != num) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
}
|
||||
//runtime:1 ms
|
||||
//memory:36.9 MB
|
||||
@ -0,0 +1,42 @@
|
||||
/*
|
||||
// Definition for a Node.
|
||||
class Node {
|
||||
public int val;
|
||||
public List<Node> neighbors;
|
||||
public Node() {
|
||||
val = 0;
|
||||
neighbors = new ArrayList<Node>();
|
||||
}
|
||||
public Node(int _val) {
|
||||
val = _val;
|
||||
neighbors = new ArrayList<Node>();
|
||||
}
|
||||
public Node(int _val, ArrayList<Node> _neighbors) {
|
||||
val = _val;
|
||||
neighbors = _neighbors;
|
||||
}
|
||||
}
|
||||
*/
|
||||
|
||||
class Solution {
|
||||
private HashMap<Node, Node> use = new HashMap <> ();
|
||||
public Node cloneGraph(Node node) {
|
||||
if (node == null) {
|
||||
return node;
|
||||
}
|
||||
|
||||
if (use.containsKey(node)) {
|
||||
return use.get(node);
|
||||
}
|
||||
|
||||
Node cloneNode = new Node(node.val, new ArrayList());
|
||||
use.put(node, cloneNode);
|
||||
|
||||
for (Node neighbor: node.neighbors) {
|
||||
cloneNode.neighbors.add(cloneGraph(neighbor));
|
||||
}
|
||||
return cloneNode;
|
||||
}
|
||||
}
|
||||
//runtime:33 ms
|
||||
//memory:38.4 MB
|
||||
@ -0,0 +1,25 @@
|
||||
/**
|
||||
* Definition for singly-linked list.
|
||||
* public class ListNode {
|
||||
* int val;
|
||||
* ListNode next;
|
||||
* ListNode(int x) { val = x; }
|
||||
* }
|
||||
*/
|
||||
class Solution {
|
||||
public int[] reversePrint(ListNode head) {
|
||||
List<Integer> list = new ArrayList<>();
|
||||
while (head != null) {
|
||||
list.add(head.val);
|
||||
head = head.next;
|
||||
}
|
||||
int size = list.size();
|
||||
int[] arr = new int[size];
|
||||
for (int i = size - 1; i >= 0; i--) {
|
||||
arr[i] = list.get(size - 1 - i);
|
||||
}
|
||||
return arr;
|
||||
}
|
||||
}
|
||||
//runtime:2 ms
|
||||
//memory:39.1 MB
|
||||
@ -0,0 +1,14 @@
|
||||
class Solution {
|
||||
public boolean containsDuplicate(int[] nums) {
|
||||
Set<Integer> set = new HashSet<>();
|
||||
for (int num : nums) {
|
||||
if (set.contains(num)) {
|
||||
return true;
|
||||
}
|
||||
set.add(num);
|
||||
}
|
||||
return false;
|
||||
}
|
||||
}
|
||||
//runtime:9 ms
|
||||
//memory:44.2 MB
|
||||
@ -0,0 +1,18 @@
|
||||
class Solution {
|
||||
public boolean containsNearbyDuplicate(int[] nums, int k) {
|
||||
if (k <= 0) {
|
||||
return false;
|
||||
}
|
||||
for (int i = 0; i < nums.length; i++) {
|
||||
for (int j = i + 1; j <= Math.min(i + k, nums.length - 1); j++) {
|
||||
if (nums[i] == nums[j]) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
}
|
||||
|
||||
//runtime:1607 ms
|
||||
//memory:50.3 MB
|
||||
@ -0,0 +1,18 @@
|
||||
class Solution {
|
||||
public int countTriples(int n) {
|
||||
int count = 0;
|
||||
for (int i = n; i > 0; i--) {
|
||||
for (int j = i - 1; j > 0; j--) {
|
||||
int sum = i * i - j * j;
|
||||
int num = (int) Math.sqrt(sum);
|
||||
if (sum == num * num) {
|
||||
count++;
|
||||
|
||||
}
|
||||
}
|
||||
}
|
||||
return count;
|
||||
}
|
||||
}
|
||||
//runtime:8 ms
|
||||
//memory:35.3 MB
|
||||
@ -0,0 +1,35 @@
|
||||
class MyHashMap {
|
||||
|
||||
int[] arr;
|
||||
|
||||
/** Initialize your data structure here. */
|
||||
public MyHashMap() {
|
||||
arr = new int[1000001];
|
||||
Arrays.fill(arr, -1);
|
||||
}
|
||||
|
||||
/** value will always be non-negative. */
|
||||
public void put(int key, int value) {
|
||||
arr[key]=value;
|
||||
}
|
||||
|
||||
/** Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key */
|
||||
public int get(int key) {
|
||||
return arr[key];
|
||||
}
|
||||
|
||||
/** Removes the mapping of the specified value key if this map contains a mapping for the key */
|
||||
public void remove(int key) {
|
||||
arr[key]=-1;
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
* Your MyHashMap object will be instantiated and called as such:
|
||||
* MyHashMap obj = new MyHashMap();
|
||||
* obj.put(key,value);
|
||||
* int param_2 = obj.get(key);
|
||||
* obj.remove(key);
|
||||
*/
|
||||
//runtime:49 ms
|
||||
//memory:45.8 MB
|
||||
@ -0,0 +1,28 @@
|
||||
class Solution {
|
||||
public int eliminateMaximum(int[] dist, int[] speed) {
|
||||
int size = dist.length;
|
||||
int[] times = new int[size];
|
||||
for (int i = 0; i < size; i++) {
|
||||
int time = dist[i] / speed[i];
|
||||
times[i] = dist[i] % speed[i] == 0 ? time - 1 : time;
|
||||
}
|
||||
Arrays.sort(times);
|
||||
Map<Integer, Integer> map = new HashMap<>();
|
||||
for (int i = 0; i < size; i++) {
|
||||
map.put(times[i], map.getOrDefault(times[i], 0) + 1);
|
||||
}
|
||||
int index = 1;
|
||||
for (int i = 0; i < size; i++) {
|
||||
if(map.containsKey(i)){
|
||||
if(map.get(i)>index){
|
||||
return i+1;
|
||||
}
|
||||
index-=map.get(i);
|
||||
}
|
||||
index++;
|
||||
}
|
||||
return size;
|
||||
}
|
||||
}
|
||||
//runtime:37 ms
|
||||
//memory:49.1 MB
|
||||
@ -0,0 +1,18 @@
|
||||
class Solution {
|
||||
public int findGCD(int[] nums) {
|
||||
int max = Integer.MIN_VALUE;
|
||||
int min = Integer.MAX_VALUE;
|
||||
for (int num : nums) {
|
||||
max = Math.max(max, num);
|
||||
min = Math.min(min, num);
|
||||
}
|
||||
for (int i = min; i >= 1; i--) {
|
||||
if (max % i == 0 && min % i == 0) {
|
||||
return i;
|
||||
}
|
||||
}
|
||||
return 1;
|
||||
}
|
||||
}
|
||||
//runtime:0 ms
|
||||
//memory:38.2 MB
|
||||
@ -0,0 +1,31 @@
|
||||
class Solution {
|
||||
public int chalkReplacer(int[] chalk, int k) {
|
||||
int temp = k;
|
||||
int length = chalk.length;
|
||||
int[] free = new int[length];
|
||||
for (int i = 0; i < length; i++) {
|
||||
if (i == 0) {
|
||||
free[i] = chalk[i];
|
||||
} else {
|
||||
free[i] += chalk[i] + free[i - 1];
|
||||
}
|
||||
temp -= chalk[i];
|
||||
if (temp < 0) {
|
||||
return i;
|
||||
}
|
||||
}
|
||||
temp %= free[length - 1];
|
||||
if (temp == 0) {
|
||||
return 0;
|
||||
}
|
||||
for (int i = 0; i < length; i++) {
|
||||
temp -= chalk[i];
|
||||
if (temp < 0) {
|
||||
return i;
|
||||
}
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
//runtime:3 ms
|
||||
//memory:50.9 MB
|
||||
@ -0,0 +1,19 @@
|
||||
class Solution {
|
||||
public String findDifferentBinaryString(String[] nums) {
|
||||
int n = nums.length;
|
||||
List<String> list = Arrays.asList(nums);
|
||||
int max = (int) Math.pow(2, n);
|
||||
for (int i = max - 1; i >= 0; i--) {
|
||||
if (!list.contains(Integer.toBinaryString(i))) {
|
||||
String temp = Integer.toBinaryString(i);
|
||||
while (temp.length() < n) {
|
||||
temp = "0" + temp;
|
||||
}
|
||||
return temp;
|
||||
}
|
||||
}
|
||||
return null;
|
||||
}
|
||||
}
|
||||
//runtime:1 ms
|
||||
//memory:36.4 MB
|
||||
@ -0,0 +1,20 @@
|
||||
class Solution {
|
||||
public int[] intersection(int[] nums1, int[] nums2) {
|
||||
|
||||
Set<Integer> set = new HashSet<>();
|
||||
for (int num : nums1) {
|
||||
set.add(num);
|
||||
}
|
||||
int index = 0;
|
||||
for (int num : nums2) {
|
||||
if (set.contains(num)) {
|
||||
set.remove(num);
|
||||
nums1[index] = num;
|
||||
index++;
|
||||
}
|
||||
}
|
||||
return Arrays.copyOf(nums1, index);
|
||||
}
|
||||
}
|
||||
//runtime:3 ms
|
||||
//memory:38.4 MB
|
||||
@ -0,0 +1,22 @@
|
||||
class Solution {
|
||||
public String maximumNumber(String num, int[] change) {
|
||||
StringBuilder str = new StringBuilder();
|
||||
int flag = 0;
|
||||
int i = 0;
|
||||
for (; i < num.length(); i++) {
|
||||
int n = num.charAt(i) - '0';
|
||||
if (n > change[n] && flag == 1) {
|
||||
break;
|
||||
}
|
||||
if (n < change[n]) {
|
||||
str.append(change[n]);
|
||||
flag = 1;
|
||||
}else{
|
||||
str.append(n);
|
||||
}
|
||||
}
|
||||
return str + num.substring(i);
|
||||
}
|
||||
}
|
||||
//runtime:12 ms
|
||||
//memory:39.3 MB
|
||||
@ -0,0 +1,60 @@
|
||||
class MaxStack {
|
||||
Stack<Integer> stack;
|
||||
Stack<Integer> max;
|
||||
|
||||
/**
|
||||
* initialize your data structure here.
|
||||
*/
|
||||
public MaxStack() {
|
||||
stack = new Stack<>();
|
||||
max = new Stack<>();
|
||||
}
|
||||
|
||||
public void push(int x) {
|
||||
stack.push(x);
|
||||
if(max.isEmpty()||x>max.peek()){
|
||||
max.push(x);
|
||||
}else{
|
||||
max.push(max.peek());
|
||||
}
|
||||
}
|
||||
|
||||
public int pop() {
|
||||
max.pop();
|
||||
return stack.pop();
|
||||
}
|
||||
|
||||
public int top() {
|
||||
return stack.peek();
|
||||
}
|
||||
|
||||
public int peekMax() {
|
||||
return max.peek();
|
||||
}
|
||||
|
||||
public int popMax() {
|
||||
int num = max.peek();
|
||||
Stack<Integer> temp = new Stack<>();
|
||||
while (stack.peek()!=num){
|
||||
temp.push(pop());
|
||||
}
|
||||
pop();
|
||||
while (!temp.isEmpty()){
|
||||
push(temp.pop());
|
||||
}
|
||||
return num;
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
* Your MaxStack object will be instantiated and called as such:
|
||||
* MaxStack obj = new MaxStack();
|
||||
* obj.push(x);
|
||||
* int param_2 = obj.pop();
|
||||
* int param_3 = obj.top();
|
||||
* int param_4 = obj.peekMax();
|
||||
* int param_5 = obj.popMax();
|
||||
*/
|
||||
|
||||
//runtime:23 ms
|
||||
//memory:41 MB
|
||||
@ -0,0 +1,36 @@
|
||||
class Solution {
|
||||
|
||||
private int max = 0;
|
||||
|
||||
public int maxCompatibilitySum(int[][] students, int[][] mentors) {
|
||||
dfs(0,students,mentors,new ArrayList<>(),0);
|
||||
return max;
|
||||
}
|
||||
|
||||
private void dfs(int index, int[][] students, int[][] mentors, List<Integer> use, int sum) {
|
||||
if (index == students.length) {
|
||||
max = Math.max(max, sum);
|
||||
return;
|
||||
}
|
||||
int[] student = students[index];
|
||||
for (int i = 0; i < mentors.length; i++) {
|
||||
if (use.contains(i)) {
|
||||
continue;
|
||||
}
|
||||
int[] mentor = mentors[i];
|
||||
int count = 0;
|
||||
for (int j = 0; j < student.length; j++) {
|
||||
if (student[j] == mentor[j]) {
|
||||
count++;
|
||||
}
|
||||
}
|
||||
use.add(i);
|
||||
sum += count;
|
||||
dfs(index + 1, students, mentors, use, sum);
|
||||
use.remove(use.size() - 1);
|
||||
sum -= count;
|
||||
}
|
||||
}
|
||||
}
|
||||
//runtime:257 ms
|
||||
//memory:36.3 MB
|
||||
@ -0,0 +1,22 @@
|
||||
class Solution {
|
||||
public long maxMatrixSum(int[][] matrix) {
|
||||
int min = Integer.MAX_VALUE;
|
||||
long sum = 0;
|
||||
long mul = 1;
|
||||
int count = 0;
|
||||
for (int[] ints : matrix) {
|
||||
for (int j = 0; j < matrix[0].length; j++) {
|
||||
sum += Math.abs(ints[j]);
|
||||
if (ints[j] != 0) {
|
||||
mul = mul * ints[j] > 0 ? 1 : -1;
|
||||
min = Math.min(min, Math.abs(ints[j]));
|
||||
} else {
|
||||
count++;
|
||||
}
|
||||
}
|
||||
}
|
||||
return mul < 0 && count == 0 ? sum - 2L * min : sum;
|
||||
}
|
||||
}
|
||||
//runtime:8 ms
|
||||
//memory:47.9 MB
|
||||
@ -0,0 +1,13 @@
|
||||
class Solution {
|
||||
public long numberOfWeeks(int[] milestones) {
|
||||
long max = 0;
|
||||
long sum = 0;
|
||||
for (int milestone : milestones) {
|
||||
sum += milestone;
|
||||
max = Math.max(max, milestone);
|
||||
}
|
||||
return sum / max >= 2 ? sum : (sum - max) * 2 + 1;
|
||||
}
|
||||
}
|
||||
//runtime:3 ms
|
||||
//memory:47.5 MB
|
||||
@ -0,0 +1,9 @@
|
||||
class Solution {
|
||||
public int maxProductDifference(int[] nums) {
|
||||
Arrays.sort(nums);
|
||||
int size = nums.length;
|
||||
return nums[size-1]*nums[size-2]-nums[0]*nums[1];
|
||||
}
|
||||
}
|
||||
//runtime:8 ms
|
||||
//memory:38.5 MB
|
||||
@ -0,0 +1,21 @@
|
||||
class Solution {
|
||||
public long minimumPerimeter(long neededApples) {
|
||||
if (neededApples == 0) {
|
||||
return 0;
|
||||
}
|
||||
if (neededApples < 12) {
|
||||
return 8;
|
||||
}
|
||||
long n = 2;
|
||||
long cur = 12;
|
||||
long sum = 12;
|
||||
while (sum < neededApples) {
|
||||
cur = cur + 12 * (n + 1);
|
||||
sum += cur;
|
||||
n += 2;
|
||||
}
|
||||
return 4 * n;
|
||||
}
|
||||
}
|
||||
//runtime:15 ms
|
||||
//memory:35.2 MB
|
||||
@ -0,0 +1,15 @@
|
||||
class Solution {
|
||||
public int minTimeToType(String word) {
|
||||
int time = 0;
|
||||
char[] chs = word.toCharArray();
|
||||
time += chs.length;
|
||||
time += Math.min(26 - Math.abs(chs[0] - 'a'), Math.abs(chs[0] - 'a'));
|
||||
for (int i = 1; i < chs.length; i++) {
|
||||
int abs = Math.abs(chs[i] - chs[i - 1]);
|
||||
time += Math.min(26 - abs, abs);
|
||||
}
|
||||
return time;
|
||||
}
|
||||
}
|
||||
//runtime:0 ms
|
||||
//memory:36.6 MB
|
||||
@ -0,0 +1,35 @@
|
||||
class MovingAverage {
|
||||
Queue<Integer> queue;
|
||||
int size;
|
||||
double sum = 0.0;
|
||||
|
||||
/**
|
||||
* Initialize your data structure here.
|
||||
*/
|
||||
public MovingAverage(int size) {
|
||||
queue = new LinkedList<>();
|
||||
this.size = size;
|
||||
}
|
||||
|
||||
public double next(int val) {
|
||||
if (queue.size() >= size) {
|
||||
sum += 1.0 * (val - queue.poll()) / size;
|
||||
} else {
|
||||
if (queue.isEmpty()) {
|
||||
sum += val;
|
||||
} else {
|
||||
sum = (sum * queue.size() + val) / (queue.size() + 1);
|
||||
}
|
||||
}
|
||||
queue.offer(val);
|
||||
return sum;
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
* Your MovingAverage object will be instantiated and called as such:
|
||||
* MovingAverage obj = new MovingAverage(size);
|
||||
* double param_1 = obj.next(val);
|
||||
*/
|
||||
//runtime:59 ms
|
||||
//memory:42.7 MB
|
||||
@ -0,0 +1,18 @@
|
||||
class Solution {
|
||||
public double myPow(double x, int n) {
|
||||
double ans=1;
|
||||
if(n<0)
|
||||
x=1/x;
|
||||
long exp=n;
|
||||
exp=Math.abs(exp);
|
||||
while(exp>0){
|
||||
if(exp%2==1)
|
||||
ans=ans*x;
|
||||
x*=x;
|
||||
exp/=2;
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
//runtime:0 ms
|
||||
//memory:36.4 MB
|
||||
File diff suppressed because one or more lines are too long
@ -0,0 +1,19 @@
|
||||
class Solution {
|
||||
public boolean makeEqual(String[] words) {
|
||||
int[] count = new int[26];
|
||||
int size = words.length;
|
||||
for (String word : words) {
|
||||
for (char ch : word.toCharArray()) {
|
||||
count[ch - 'a']++;
|
||||
}
|
||||
}
|
||||
for (int i = 0; i < 26; i++) {
|
||||
if (count[i] % size > 0) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
}
|
||||
//runtime:2 ms
|
||||
//memory:38.3 MB
|
||||
@ -0,0 +1,12 @@
|
||||
class Solution {
|
||||
public int[] sortedSquares(int[] nums) {
|
||||
for (int i = 0; i < nums.length; i++) {
|
||||
nums[i]*=nums[i];
|
||||
}
|
||||
Arrays.sort(nums);
|
||||
return nums;
|
||||
}
|
||||
}
|
||||
|
||||
//runtime:2 ms
|
||||
//memory:40.2 MB
|
||||
@ -0,0 +1,31 @@
|
||||
class Solution {
|
||||
public int getLucky(String s, int k) {
|
||||
int sum = 0;
|
||||
int count = 0;
|
||||
for (char ch : s.toCharArray()) {
|
||||
int num = ch - 'a' + 1;
|
||||
if (num > 9) {
|
||||
sum += num / 10 + num % 10;
|
||||
} else {
|
||||
sum += num;
|
||||
}
|
||||
}
|
||||
if (sum < 10 || k == 1) {
|
||||
return sum;
|
||||
}
|
||||
for (int i = 1; i < k; i++) {
|
||||
int result = 0;
|
||||
while (sum > 9) {
|
||||
result += sum % 10;
|
||||
sum /= 10;
|
||||
}
|
||||
sum += result;
|
||||
if (sum < 10) {
|
||||
break;
|
||||
}
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
}
|
||||
//runtime:0 ms
|
||||
//memory:36.8 MB
|
||||
@ -0,0 +1,20 @@
|
||||
class Solution {
|
||||
public int[] kWeakestRows(int[][] mat, int k) {
|
||||
int m = mat.length, n = mat[0].length;
|
||||
int[][] all = new int[m][2];
|
||||
for (int i = 0; i < m; i++) {
|
||||
int cur = 0;
|
||||
for (int j = 0; j < n; j++) cur += mat[i][j];
|
||||
all[i] = new int[]{cur, i};
|
||||
}
|
||||
Arrays.sort(all, (a, b)->{
|
||||
if (a[0] != b[0]) return a[0] - b[0];
|
||||
return a[1] - b[1];
|
||||
});
|
||||
int[] ans = new int[k];
|
||||
for (int i = 0; i < k; i++) ans[i] = all[i][1];
|
||||
return ans;
|
||||
}
|
||||
}
|
||||
//runtime:2 ms
|
||||
//memory:39.5 MB
|
||||
@ -0,0 +1,46 @@
|
||||
class Solution {
|
||||
public int smallestChair(int[][] times, int targetFriend) {
|
||||
int[] target = times[targetFriend];
|
||||
Arrays.sort(times, new Comparator<int[]>() {
|
||||
public int compare(int[] a, int[] b) {
|
||||
return a[0] - b[0];
|
||||
}
|
||||
});
|
||||
int size = 0;
|
||||
for (int i = 0; i < times.length; i++) {
|
||||
if (times[i][0] == target[0]) {
|
||||
size = i;
|
||||
break;
|
||||
}
|
||||
}
|
||||
int[] arr = new int[size + 1];
|
||||
List<Integer> use = new ArrayList<>();
|
||||
int index = 0;
|
||||
int start = times[0][0];
|
||||
for (int[] time : times) {
|
||||
for (int i = 0; i < index; i++) {
|
||||
if (arr[i] > 0) {
|
||||
arr[i] -= time[0] - start;
|
||||
if (arr[i] <= 0) {
|
||||
use.add(i);
|
||||
Collections.sort(use);
|
||||
}
|
||||
}
|
||||
}
|
||||
start = time[0];
|
||||
if (time[0] == target[0]) {
|
||||
return use.size() > 0 ? use.get(0) : index;
|
||||
}
|
||||
if (use.size() > 0) {
|
||||
arr[use.get(0)] = time[1] - time[0];
|
||||
use.remove(0);
|
||||
} else {
|
||||
arr[index] = time[1] - time[0];
|
||||
index++;
|
||||
}
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
//runtime:433 ms
|
||||
//memory:46.5 MB
|
||||
@ -0,0 +1,20 @@
|
||||
class Solution {
|
||||
public boolean isThree(int n) {
|
||||
int flag = 0;
|
||||
if (n <= 2) {
|
||||
return false;
|
||||
}
|
||||
int num = n / 2;
|
||||
for (int i = 2; i <= num; i++) {
|
||||
if (n % i == 0) {
|
||||
if (flag == 1) {
|
||||
return false;
|
||||
}
|
||||
flag = 1;
|
||||
}
|
||||
}
|
||||
return flag == 1;
|
||||
}
|
||||
}
|
||||
//runtime:0 ms
|
||||
//memory:35.3 MB
|
||||
Loading…
Reference in New Issue
Block a user