363:矩形区域不超过 K 的最大数值和(doing)

LeetCode/src/main/java/leetcode/editor/cn/MaxSumOfRectangleNoLargerThanK.java

@@ -0,0 +1,91 @@
+//给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。 
+//
+// 题目数据保证总会存在一个数值和不超过 k 的矩形区域。 
+//
+// 
+//
+// 示例 1： 
+//
+// 
+//输入：matrix = [[1,0,1],[0,-2,3]], k = 2
+//输出：2
+//解释：蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。
+// 
+//
+// 示例 2： 
+//
+// 
+//输入：matrix = [[2,2,-1]], k = 3
+//输出：3
+// 
+//
+// 
+//
+// 提示： 
+//
+// 
+// m == matrix.length 
+// n == matrix[i].length 
+// 1 <= m, n <= 100 
+// -100 <= matrix[i][j] <= 100 
+// -105 <= k <= 105 
+// 
+//
+// 
+//
+// 进阶：如果行数远大于列数，该如何设计解决方案？ 
+// Related Topics 队列 二分查找 动态规划 
+// 👍 225 👎 0
+
+package leetcode.editor.cn;
+
+import java.util.ArrayList;
+import java.util.List;
+
+//363:矩形区域不超过 K 的最大数值和
+public class MaxSumOfRectangleNoLargerThanK {
+    public static void main(String[] args) {
+        //测试代码
+        Solution solution = new MaxSumOfRectangleNoLargerThanK().new Solution();
+//        //2
+//        System.out.println(solution.maxSumSubmatrix(new int[][]{{1, 0, 1}, {0, -2, 3}}, 2));
+//        //3
+//        System.out.println(solution.maxSumSubmatrix(new int[][]{{2, 2, -1}}, 3));
+//        //-1
+//        System.out.println(solution.maxSumSubmatrix(new int[][]{{2, 2, -1}}, 0));
+        //8
+        System.out.println(solution.maxSumSubmatrix(new int[][]{{5, -4, -3, 4}, {-3, -4, 4, 5}, {5, 1, 5, -4}}, 8));
+    }
+
+    //力扣代码
+    //leetcode submit region begin(Prohibit modification and deletion)
+    class Solution {
+        public int maxSumSubmatrix(int[][] matrix, int k) {
+            int xLength = matrix.length;
+            int yLength = matrix[0].length;
+            int[][] sums = new int[xLength][yLength];
+            for (int i = 0; i < xLength; i++) {
+                int sum = 0;
+                for (int j = 0; j < yLength; j++) {
+                    sum += matrix[i][j];
+                    sums[i][j] = sum;
+                }
+            }
+            int max = Integer.MIN_VALUE;
+            for (int i = yLength - 1; i >= 0; i--) {
+                for (int l = 0; l <= i; l++) {
+                    int sum = 0;
+                    for (int j = 0; j < xLength; j++) {
+                        sum += l == 0 ? sums[j][i] : sums[j][i] - sums[j][i-l];
+                        if (sum <= k) {
+                            max = Math.max(max, sum);
+                        }
+                    }
+                }
+            }
+            return max;
+        }
+    }
+//leetcode submit region end(Prohibit modification and deletion)
+
+}

LeetCode/src/main/java/leetcode/editor/cn/MaxSumOfRectangleNoLargerThanK.md

@@ -0,0 +1,37 @@
+<p>给你一个 <code>m x n</code> 的矩阵 <code>matrix</code> 和一个整数 <code>k</code> ，找出并返回矩阵内部矩形区域的不超过 <code>k</code> 的最大数值和。</p>
+
+<p>题目数据保证总会存在一个数值和不超过 <code>k</code> 的矩形区域。</p>
+
+<p> </p>
+
+<p><strong>示例 1：</strong></p>
+<img alt="" src="https://assets.leetcode.com/uploads/2021/03/18/sum-grid.jpg" style="width: 255px; height: 176px;" />
+<pre>
+<strong>输入：</strong>matrix = [[1,0,1],[0,-2,3]], k = 2
+<strong>输出：</strong>2
+<strong>解释：</strong>蓝色边框圈出来的矩形区域 <code>[[0, 1], [-2, 3]]</code> 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。
+</pre>
+
+<p><strong>示例 2：</strong></p>
+
+<pre>
+<strong>输入：</strong>matrix = [[2,2,-1]], k = 3
+<strong>输出：</strong>3
+</pre>
+
+<p> </p>
+
+<p><strong>提示：</strong></p>
+
+<ul>
+	<li><code>m == matrix.length</code></li>
+	<li><code>n == matrix[i].length</code></li>
+	<li><code>1 <= m, n <= 100</code></li>
+	<li><code>-100 <= matrix[i][j] <= 100</code></li>
+	<li><code>-10<sup>5</sup> <= k <= 10<sup>5</sup></code></li>
+</ul>
+
+<p> </p>
+
+<p><strong>进阶：</strong>如果行数远大于列数，该如何设计解决方案？</p>
+<div><div>Related Topics</div><div><li>队列</li><li>二分查找</li><li>动态规划</li></div></div>\n<div><li>👍 225</li><li>👎 0</li></div>

LeetCode/src/main/java/leetcode/editor/cn/doc/363-ju-xing-qu-yu-bu-chao-guo-k-de-zui-d-f18a.md

@@ -0,0 +1,74 @@
+思路: 
+
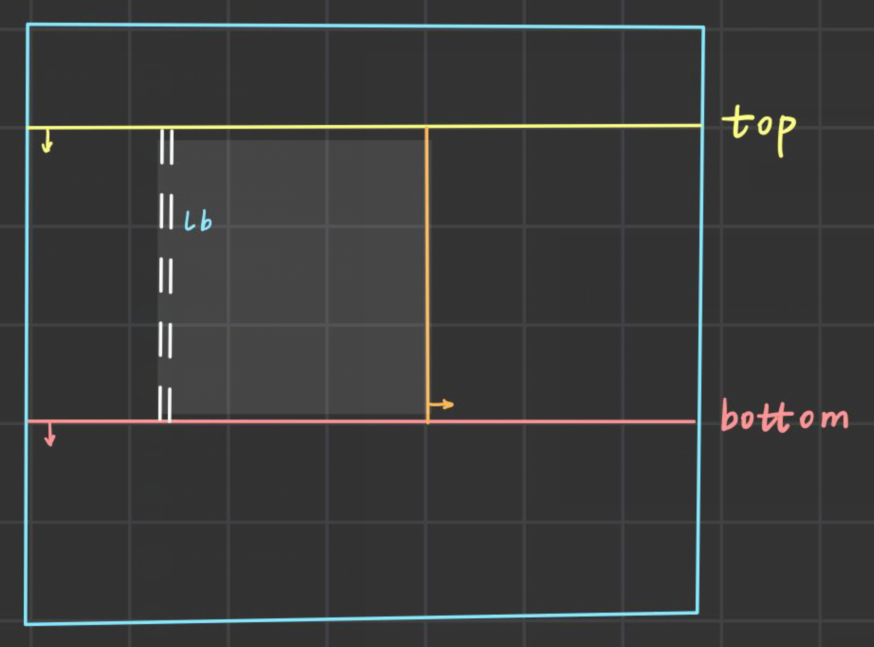
+先找好遍历顺序, top和bottom分别为行的上下界, 然后对列进行遍历, 利用前缀和+二分查找的方式更新ans
+
+![](https://pic.leetcode-cn.com/1619058643-fkFedw-image.png)
+
+
+### 1 | 二分查找+一维前缀和
+
+这种方式在行遍历时先用一个sum[]保存每一列的和, 然后在列遍历的过程中动态维护前缀和
+
+```cpp
+class Solution {
+public:
+    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
+        int m = matrix.size(), n = matrix[0].size(), ans = INT_MIN;
+        // top
+        for (int i = 0; i < m; ++i) {
+            // bottom
+            vector<int> sum(n, 0);
+            for (int j = i; j < m; ++j) {
+                set<int> st{0};
+                int r = 0;
+                for (int z = 0; z < n; ++z) {
+                    sum[z] += matrix[j][z];                    
+                    r += sum[z];
+                    auto lb = st.lower_bound(r - k);
+                    if (lb != st.end()) {
+                        ans = max(ans, r - *lb);
+                    }
+                    st.insert(r);
+                }
+            }
+        }
+        return ans;
+    }
+};
+```
+
+### 2 | 二分查找+二维前缀和(积分图)
+
+先对矩阵进行预处理, 可以减少动态维护前缀和时候重复计算的开销, 但是增大了空间复杂度
+
+```cpp
+class Solution {
+public:
+    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
+        int m = matrix.size(), n = matrix[0].size(), ans = INT_MIN;
+        vector<vector<int>> pre(m + 1, vector<int>(n + 1, 0));
+        // 积分图
+        for (int i = 1; i <= m; ++i) {
+            for (int j = 1; j <= n; ++j) {
+                pre[i][j] = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] + matrix[i - 1][j - 1];
+            }
+        }
+        // top
+        for (int i = 1; i <= m; ++i) {
+            // bottom
+            for (int j = i; j <= m; ++j) {
+                set<int> st{0};
+                for (int z = 1; z <= n; ++z) {
+                    int r = pre[j][z] - pre[i - 1][z];
+                    auto lb = st.lower_bound(r - k);
+                    if (lb != st.end()) {
+                        ans = max(ans, r - *lb);
+                    }
+                    st.insert(r);
+                }
+            }
+        }
+        return ans;
+    }
+};
+```