huangge1199/leet-code
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity

周赛264

Browse Source
This commit is contained in:
huangge1199@hotmail.com 2021-10-24 12:03:22 +08:00
parent 3868362349
commit 3b2158cc99
22 changed files with 4924 additions and 0 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

62
src/main/java/contest/y2021/m10/week/Solution264.java Normal file
View File

@ -0,0 +1,62 @@
package contest.y2021.m10.week;
import com.sun.java.swing.plaf.windows.WindowsTextAreaUI;
import javax.swing.*;
import java.util.*;
import java.util.regex.Pattern;
/**
* @description:
* @author: Administrator
* @date: 2021/8/22-10:29
*/
public class Solution264 {
public static void main(String[] args) {
Solution264 solution = new Solution264();
}
public int countValidWords(String sentence) {
String regex = "[a-z]*([a-z]+[-][a-z]+)?[!.,]?";
if (!sentence.contains(" ")) {
if (Pattern.compile(regex).matcher(sentence).matches()) {
return 1;
} else {
return 0;
}
}
String[] strs = sentence.split(" ");
int count = 0;
for (String str : strs) {
if (!str.equals("") && Pattern.compile(regex).matcher(str).matches()) {
count++;
}
}
return count;
}
public int nextBeautifulNumber(int n) {
for (int i = n + 1; ; i++) {
int[] arrs = new int[10];
int temp = i;
while (temp > 9 && temp % 10 > 0) {
arrs[temp % 10]++;
temp /= 10;
}
if (temp > 9) {
continue;
}
arrs[temp]++;
boolean bl = true;
for (int j = 1; j < 10; j++) {
if (arrs[j] > 0 && arrs[j] != j) {
bl = false;
break;
}
}
if (bl) {
return i;
}
}
}
}

26
src/main/java/leetcode/editor/cn/doc/solution/3ms-99-xian-pai-xu-zai-chuan-cha-by-wang-o7pm.lcv Normal file
View File

@ -0,0 +1,26 @@
### 解题思路
* 数组按照从小到大排序后，从中间切分,比如 123456 切分后123，456 穿插进行后142536符合题意
* 但是1223这种就不行了，但是穿插规则可以变一下，两部分逆序穿插，即2 3 1 2
### 代码
* java
```java
class Solution {
public void wiggleSort(int[] nums) {
int[] help = nums.clone(); //不能写成int[] help = nums,排序后两个数组都改变
Arrays.sort(help);
int N = nums.length;
//比如123456
for (int i = 1; i < nums.length; i += 2) {
nums[i] = help[--N]; //遍历完成后 x 6 x 5 x 4
}
for (int i = 0; i < nums.length; i += 2) {
nums[i] = help[--N]; //便利完成后 3 6 2 5 1 4
}
}
}
```

250
src/main/java/leetcode/editor/cn/doc/solution/bu-han-lian-xu-1de-fei-fu-zheng-shu-by-l-9l86.lcv Normal file
View File

@ -0,0 +1,250 @@
#### 方法一：动态规划
**思路**
因为正整数 $n$ 可以取到 $10^9$，所以显然是不可能通过暴力遍历从 $1$ 到 $n$ 的所有正整数来计算答案的。直观上，我们也可以感觉到，在暴力遍历的过程中，有非常多的计算是重复的。因此，我们考虑通过优化暴力遍历来解决这个问题。
为了形象地将重复计算的部分找出来，我们不妨将小于等于 $n$ 的非负整数用 $01$ 字典树的形式表示，其中的每一条从根结点到叶结点的路径都是一个小于等于 $n$ 的非负整数（包含前导 $0$）。
于是，题目可以转化为：在由所有小于等于 $n$ 的非负整数构成的 $01$ 字典树中，找出不包含连续 $1$ 的从根结点到叶结点的路径数量。
![g1](https://assets.leetcode-cn.com/solution-static/600/g1.png)
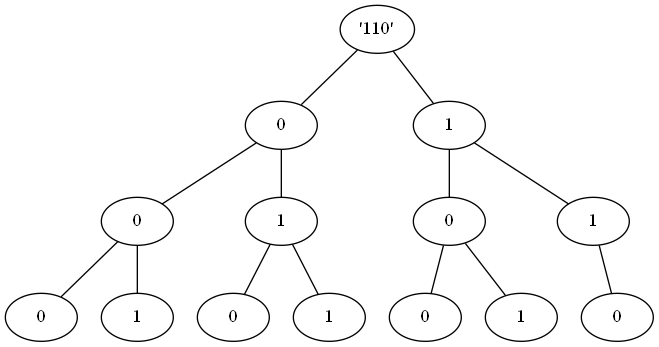
以 $n = 6 = (110)_2$ 为例，我们可以发现：
* 对于 $01$ 字典树中的两个节点 $n_1$ 和 $n_2$，如果它们的高度相同，节点的值也相同，并且以它们为根结点的两棵子树都是满二叉树，那么它们包含的无连续 $1$ 的从根结点到叶结点的路径个数是相同的。
* 对于 $01$ 字典树中的两个结点 $n_1$ 和 $n_2$，如果 $n_2$ 是 $n_1$ 的子结点，并且它们的值都是 $1$，那么所有经过 $n_1$ 和 $n_2$ 的从根结点到叶结点的路径都一定包含连续的 $1$。
注意到由小于等于 $n$ 的非负整数构成的 $01$ 字典树是完全二叉树。于是有：如果某个结点包含两个子结点，那么其左子结点为根结点是 $0$ 的满二叉树，其右子结点为根结点是 $1$ 的完全二叉树；如果某个结点只有一个子结点，那么其左子结点为根结点是 $0$ 的完全二叉树。
我们在计算不包含连续 $1$ 的从根结点到叶结点的路径数量时，可以不断地将字典树拆分为根结点为 $0$ 的满二叉树和根结点不定的完全二叉树。
于是，题目被拆分为以下两个子问题：
* 问题 $1$：如何计算根结点为 $0$ 的满二叉树中，不包含连续 $1$ 的从根结点到叶结点的路径数量。
* 问题 $2$：如何将将字典树拆分为根结点为 $0$ 的满二叉树和根结点不定的完全二叉树。
**算法**
首先解决第 $1$ 个问题。
我们发现，在高度为 $t$、根结点为 $0$ 的满二叉树中：其左子结点是高度为 $t-1$、根结点为 $0$ 的满二叉树。其右子结点是高度为 $t-1$、根结点为 $1$ 的满二叉树；但是因为路径中不能有连续 $1$，所以右子结点下只有其左子结点包含的从根结点到叶结点的路径才符合要求，而其左子结点是高度为 $t-2$、根结点为 $0$ 的满二叉树。
于是，高度为 $t$、根结点为 $0$ 的满二叉树中不包含连续 $1$ 的从根结点到叶结点的路径数量，等于高度为 $t-1$、根结点为 $0$ 的满二叉树中的路径数量与高度为 $t-2$，根结点为 $0$ 的满二叉树中的路径数量之和。因此，这个问题可以通过动态规划解决：
状态：$\textit{dp}[t]$。$\textit{dp}[t]$ 表示高度为 $t-1$、根结点为 $0$ 的满二叉树中，不包含连续 $1$ 的从根结点到叶结点的路径数量。
状态转移方程：
$$
dp[t] =
\begin
dp[t-1] + dp[t-2], \quad t \ge 2 \\
1, \quad t < 2
\end
$$
接着解决第 $2$ 个问题。
考虑到 $01$ 字典树作为完全二叉树所具有的性质，我们可以从根结点开始处理。如果当前结点包含两个子结点，则用问题 $1$ 的解决方法计算其左子结点中不包含连续 $1$ 的从根结点到叶结点的路径数量，并继续处理其右子结点；如果当前结点只包含一个左子结点，那么继续处理其左子结点。
在实现中，需要注意如果已经出现连续 $1$ 则不用继续处理；另外，叶结点没有子结点，需要作为特殊情况单独处理。
**代码**
* [sol1-Python3]
```Python
class Solution:
def findIntegers(self, n: int) -> int:
dp = [0] * 31
dp[0] = 1
dp[1] = 1
for i in range(2, 31):
dp[i] = dp[i - 1] + dp[i - 2]
pre = 0
res = 0
for i in range(29, -1, -1):
val = (1 << i)
if n & val:
res += dp[i + 1]
if pre == 1:
break
pre = 1
else:
pre = 0
if i == 0:
res += 1
return res
```
* [sol1-Java]
```Java
class Solution {
public int findIntegers(int n) {
int[] dp = new int[31];
dp[0] = dp[1] = 1;
for (int i = 2; i < 31; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
int pre = 0, res = 0;
for (int i = 29; i >= 0; --i) {
int val = 1 << i;
if ((n & val) != 0) {
res += dp[i + 1];
if (pre == 1) {
break;
}
pre = 1;
} else {
pre = 0;
}
if (i == 0) {
++res;
}
}
return res;
}
}
```
* [sol1-C#]
```C#
public class Solution {
public int FindIntegers(int n) {
int[] dp = new int[31];
dp[0] = dp[1] = 1;
for (int i = 2; i < 31; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
int pre = 0, res = 0;
for (int i = 29; i >= 0; --i) {
int val = 1 << i;
if ((n & val) != 0) {
res += dp[i + 1];
if (pre == 1) {
break;
}
pre = 1;
} else {
pre = 0;
}
if (i == 0) {
++res;
}
}
return res;
}
}
```
* [sol1-C++]
```C++
class Solution {
public:
int findIntegers(int n) {
vector<int> dp(31);
dp[0] = dp[1] = 1;
for (int i = 2; i < 31; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
int pre = 0, res = 0;
for (int i = 29; i >= 0; --i) {
int val = 1 << i;
if ((n & val) != 0) {
res += dp[i + 1];
if (pre == 1) {
break;
}
pre = 1;
} else {
pre = 0;
}
if (i == 0) {
++res;
}
}
return res;
}
};
```
* [sol1-JavaScript]
```JavaScript
var findIntegers = function(n) {
const dp = new Array(31).fill(0);
dp[0] = dp[1] = 1;
for (let i = 2; i < 31; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
let pre = 0, res = 0;
for (let i = 29; i >= 0; --i) {
let val = 1 << i;
if ((n & val) !== 0) {
res += dp[i + 1];
if (pre === 1) {
break;
}
pre = 1;
} else {
pre = 0;
}
if (i === 0) {
++res;
}
}
return res;
};
```
* [sol1-Golang]
```go
func findIntegers(n int) (ans int) {
dp := [31]int{1, 1}
for i := 2; i < 31; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
for i, pre := 29, 0; i >= 0; i-- {
val := 1 << i
if n&val > 0 {
ans += dp[i+1]
if pre == 1 {
break
}
pre = 1
} else {
pre = 0
}
if i == 0 {
ans++
}
}
return
}
```
**复杂度分析**
- 时间复杂度：$O(\log (n_{\max}))$，其中 $n_{\max}$ 表示 $n$ 的最大值，本题中 $n=10^9$，$\log (n_{\max}) \approx 30$。我们需要 $O(\log (n_{\max}))$ 的时间来计算根结点为 $0$ 的满二叉树中不包含连续 $1$ 的从根结点到叶结点的路径数量，以及 $O(\log (n_{\max}))$ 的时间来迭代地处理每一个二进制位。
- 空间复杂度：$O(\log (n_{\max}))$。我们需要额外的一个数组保存根结点为 $0$ 的满二叉树中不包含连续 $1$ 的路径数量。

162
src/main/java/leetcode/editor/cn/doc/solution/cong-zui-ji-chu-de-jiang-qi-ru-he-zuo-dao-jun-yun-.lcv Normal file
View File

@ -0,0 +1,162 @@
因为是第一次接触到这样的题目，毫无思绪，对官方题解也是“不知道为什么要这么做”。看过一些题解之后才逐渐明白，现在让我自己来写题解，我打算先从简单的开始讲起。
### Part 1
假设已知`rand2()`可以**均匀**的生成[1,2]的随机数，现在想均匀的生成[1,4]的随机数，该如何考虑？
我想如果你也像我一样第一次接触这个问题，那么很可能会这么考虑——令两个`rand2()`相加，再做一些必要的边角处理。如下：
*
```
rand2() + rand2() = ? ==> [2,4]
1 + 1 = 2
1 + 2 = 3
2 + 1 = 3
2 + 2 = 4
// 为了把生成随机数的范围规约成[1,n]，于是在上一步的结果后减1
(rand2()-1) + rand2() = ? ==> [1,3]
0 + 1 = 1
0 + 2 = 2
1 + 1 = 2
1 + 2 = 3
```
可以看到，使用这种方法处理的结果，最致命的点在于——其**生成的结果不是等概率的**。在这个简单的例子中，产生2的概率是50%，而产生1和3的概率则分别是25%。原因当然也很好理解，由于某些值会有多种组合，因此仅靠简单的相加处理会导致结果不是等概率的。
因此，我们需要考虑其他的方法了。
仔细观察上面的例子，我们尝试对 `(rand2()-1)` 这部分乘以 2，改动后如下：
*
```
(rand2()-1) × 2 + rand2() = ? ==> [1,3]
0 + 1 = 1
0 + 2 = 2
2 + 1 = 3
2 + 2 = 4
```
神奇的事情发生了，奇怪的知识增加了。通过这样的处理，得到的结果恰是[1,4]的范围，并且每个数都是等概率取到的。因此，使用这种方法，可以通过`rand2()`实现`rand4()`。
也许这么处理只是我运气好，而不具有普适性？那就多来尝试几个例子。比如：
*
```
(rand9()-1) × 7 + rand7() = result
a b
```
为了表示方便，现将`rand9()-1`表示为a，将`rand7()`表示为b。计算过程表示成二维矩阵，如下：
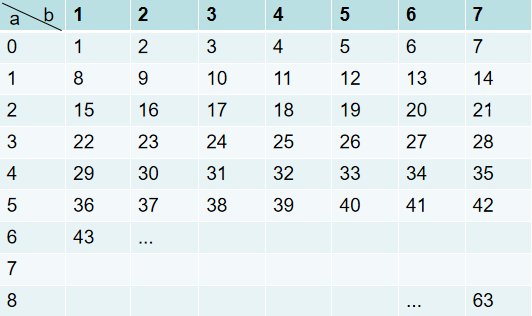
![image.png](https://pic.leetcode-cn.com/b3a6cfbc8e1c07a46db94f2af7b45935daf0b65c26649ce1b564e6ccfdf5cecf-image.png)
可以看到，这个例子可以等概率的生成[1,63]范围的随机数。再提炼一下，可以得到这样一个规律：
*
```
已知 rand_N() 可以等概率的生成[1, N]范围的随机数
那么：
(rand_X() - 1) × Y + rand_Y() ==> 可以等概率的生成[1, X * Y]范围的随机数
即实现了 rand_XY()
```
### Part 2
那么想到通过`rand4()`来实现`rand2()`呢？这个就很简单了，已知`rand4()`会均匀产生[1,4]的随机数，通过取余，再加1就可以了。如下所示，结果也是等概率的。
*
```
rand4() % 2 + 1 = ?
1 % 2 + 1 = 2
2 % 2 + 1 = 1
3 % 2 + 1 = 2
4 % 2 + 1 = 1
```
事实上，只要`rand_N()`中N是2的倍数，就都可以用来实现`rand2()`，反之，若N不是2的倍数，则产生的结果不是等概率的。比如：
*
```
rand6() % 2 + 1 = ?
1 % 2 + 1 = 2
2 % 2 + 1 = 1
3 % 2 + 1 = 2
4 % 2 + 1 = 1
5 % 2 + 1 = 2
6 % 2 + 1 = 1
rand5() % 2 + 1 = ?
1 % 2 + 1 = 2
2 % 2 + 1 = 1
3 % 2 + 1 = 2
4 % 2 + 1 = 1
5 % 2 + 1 = 2
```
### Part 3
ok，现在回到本题中。已知`rand7()`，要求通过`rand7()`来实现`rand10()`。
有了前面的分析，**要实现`rand10()`，就需要先实现`rand_N()`，并且保证N大于10且是10的倍数。这样再通过`rand_N() % 10 + 1` 就可以得到[1,10]范围的随机数了**。
而实现`rand_N()`，我们可以通过part 1中所讲的方法对`rand7()`进行改造，如下：
*
```
(rand7()-1) × 7 + rand7() ==> rand49()
```
但是这样实现的N不是10的倍数啊！这该怎么处理？这里就涉及到了“**拒绝采样**”的知识了，也就是说，如果某个采样结果不在要求的范围内，则丢弃它。基于上面的这些分析，再回头看下面的代码，想必是不难理解了。
*
```
class Solution extends SolBase {
public int rand10() {
while(true) {
int num = (rand7() - 1) * 7 + rand7(); // 等概率生成[1,49]范围的随机数
if(num <= 40) return num % 10 + 1; // 拒绝采样，并返回[1,10]范围的随机数
}
}
}
```
### Part 4: 优化
这部分具体的代码是参考官方题解的，不过是我自己在理解了part 1和part 2之后才看懂的，一开始看真不知道为什么（/(ㄒoㄒ)/~~...
根据part 1的分析，我们已经知道`(rand7() - 1) * 7 + rand7()` 等概率生成[1,49]范围的随机数。而由于我们需要的是10的倍数，因此，不得不舍弃掉[41, 49]这9个数。优化的点就始于——我们能否利用这些范围外的数字，以减少丢弃的值，提高命中率总而提高随机数生成效率。
*
```
class Solution extends SolBase {
public int rand10() {
while(true) {
int a = rand7();
int b = rand7();
int num = (a-1)*7 + b; // rand 49
if(num <= 40) return num % 10 + 1; // 拒绝采样
a = num - 40; // rand 9
b = rand7();
num = (a-1)*7 + b; // rand 63
if(num <= 60) return num % 10 + 1;
a = num - 60; // rand 3
b = rand7();
num = (a-1)*7 + b; // rand 21
if(num <= 20) return num % 10 + 1;
}
}
}
```

733
src/main/java/leetcode/editor/cn/doc/solution/dan-ci-sou-suo-ii-by-leetcode-solution-7494.lcv Normal file
View File

@ -0,0 +1,733 @@
#### 方法一：回溯 + 字典树
**预备知识**
前缀树（字典树）是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。前缀树可以用 $O(|S|)$ 的时间复杂度完成如下操作，其中 $|S|$ 是插入字符串或查询前缀的长度：
- 向前缀树中插入字符串 $\textit{word}$；
- 查询前缀串 $\textit{prefix}$ 是否为已经插入到前缀树中的任意一个字符串 $\textit{word}$ 的前缀；
前缀树的实现可以参考「[208. 实现 Trie (前缀树) 的官方题解](https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/shi-xian-trie-qian-zhui-shu-by-leetcode-ti500/)」。
**思路和算法**
根据题意，我们需要逐个遍历二维网格中的每一个单元格；然后搜索从该单元格出发的所有路径，找到其中对应 $\textit{words}$ 中的单词的路径。因为这是一个回溯的过程，所以我们有如下算法：
- 遍历二维网格中的所有单元格。
- 深度优先搜索所有从当前正在遍历的单元格出发的、由相邻且不重复的单元格组成的路径。因为题目要求同一个单元格内的字母在一个单词中不能被重复使用；所以我们在深度优先搜索的过程中，每经过一个单元格，都将该单元格的字母临时修改为特殊字符（例如 `#`），以避免再次经过该单元格。
- 如果当前路径是 $\textit{words}$ 中的单词，则将其添加到结果集中。如果当前路径是 $words$ 中任意一个单词的前缀，则继续搜索；反之，如果当前路径不是 $words$ 中任意一个单词的前缀，则剪枝。我们可以将 $\textit{words}$ 中的所有字符串先添加到前缀树中，而后用 $O(|S|)$ 的时间复杂度查询当前路径是否为 $\textit{words}$ 中任意一个单词的前缀。
在具体实现中，我们需要注意如下情况：
- 因为同一个单词可能在多个不同的路径中出现，所以我们需要使用哈希集合对结果集去重。
- 在回溯的过程中，我们不需要每一步都判断完整的当前路径是否是 $words$ 中任意一个单词的前缀；而是可以记录下路径中每个单元格所对应的前缀树结点，每次只需要判断新增单元格的字母是否是上一个单元格对应前缀树结点的子结点即可。
**代码**
* [sol1-Python3]
```Python
from collections import defaultdict
class Trie:
def __init__(self):
self.children = defaultdict(Trie)
self.word = ""
def insert(self, word):
cur = self
for c in word:
cur = cur.children[c]
cur.is_word = True
cur.word = word
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
trie = Trie()
for word in words:
trie.insert(word)
def dfs(now, i1, j1):
if board[i1][j1] not in now.children:
return
ch = board[i1][j1]
now = now.children[ch]
if now.word != "":
ans.add(now.word)
board[i1][j1] = "#"
for i2, j2 in [(i1 + 1, j1), (i1 - 1, j1), (i1, j1 + 1), (i1, j1 - 1)]:
if 0 <= i2 < m and 0 <= j2 < n:
dfs(now, i2, j2)
board[i1][j1] = ch
ans = set()
m, n = len(board), len(board[0])
for i in range(m):
for j in range(n):
dfs(trie, i, j)
return list(ans)
```
* [sol1-Java]
```Java
class Solution {
int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
public List<String> findWords(char[][] board, String[] words) {
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
Set<String> ans = new HashSet<String>();
for (int i = 0; i < board.length; ++i) {
for (int j = 0; j < board[0].length; ++j) {
dfs(board, trie, i, j, ans);
}
}
return new ArrayList<String>(ans);
}
public void dfs(char[][] board, Trie now, int i1, int j1, Set<String> ans) {
if (!now.children.containsKey(board[i1][j1])) {
return;
}
char ch = board[i1][j1];
now = now.children.get(ch);
if (!"".equals(now.word)) {
ans.add(now.word);
}
board[i1][j1] = '#';
for (int[] dir : dirs) {
int i2 = i1 + dir[0], j2 = j1 + dir[1];
if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0].length) {
dfs(board, now, i2, j2, ans);
}
}
board[i1][j1] = ch;
}
}
class Trie {
String word;
Map<Character, Trie> children;
boolean isWord;
public Trie() {
this.word = "";
this.children = new HashMap<Character, Trie>();
}
public void insert(String word) {
Trie cur = this;
for (int i = 0; i < word.length(); ++i) {
char c = word.charAt(i);
if (!cur.children.containsKey(c)) {
cur.children.put(c, new Trie());
}
cur = cur.children.get(c);
}
cur.word = word;
}
}
```
* [sol1-C#]
```C#
public class Solution {
int[][] dirs = new int[][] {
new int[]{1, 0},
new int[]{-1, 0},
new int[]{0, 1},
new int[]{0, -1}
};
public IList<string> FindWords(char[][] board, string[] words) {
Trie trie = new Trie();
foreach (string word in words) {
trie.Insert(word);
}
ISet<string> ans = new HashSet<string>();
for (int i = 0; i < board.Length; ++i) {
for (int j = 0; j < board[0].Length; ++j) {
DFS(board, trie, i, j, ans);
}
}
return new List<string>(ans);
}
void DFS(char[][] board, Trie now, int i1, int j1, ISet<string> ans) {
if (!now.children.ContainsKey(board[i1][j1])) {
return;
}
char ch = board[i1][j1];
now = now.children[ch];
if (!"".Equals(now.word)) {
ans.Add(now.word);
}
board[i1][j1] = '#';
foreach (int[] dir in dirs) {
int i2 = i1 + dir[0], j2 = j1 + dir[1];
if (i2 >= 0 && i2 < board.Length && j2 >= 0 && j2 < board[0].Length) {
DFS(board, now, i2, j2, ans);
}
}
board[i1][j1] = ch;
}
}
class Trie {
public string word;
public Dictionary<char, Trie> children;
public bool isWord;
public Trie() {
this.word = "";
this.children = new Dictionary<char, Trie>();
}
public void Insert(string word) {
Trie cur = this;
foreach (char c in word) {
if (!cur.children.ContainsKey(c)) {
cur.children.Add(c, new Trie());
}
cur = cur.children[c];
}
cur.word = word;
}
}
```
* [sol1-Golang]
```go
type Trie struct {
children [26]*Trie
word string
}
func (t *Trie) Insert(word string) {
node := t
for _, ch := range word {
ch -= 'a'
if node.children[ch] == nil {
node.children[ch] = &Trie{}
}
node = node.children[ch]
}
node.word = word
}
var dirs = []struct{ x, y int }{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
func findWords(board [][]byte, words []string) []string {
t := &Trie{}
for _, word := range words {
t.Insert(word)
}
m, n := len(board), len(board[0])
seen := map[string]bool{}
var dfs func(node *Trie, x, y int)
dfs = func(node *Trie, x, y int) {
ch := board[x][y]
node = node.children[ch-'a']
if node == nil {
return
}
if node.word != "" {
seen[node.word] = true
}
board[x][y] = '#'
for _, d := range dirs {
nx, ny := x+d.x, y+d.y
if 0 <= nx && nx < m && 0 <= ny && ny < n && board[nx][ny] != '#' {
dfs(node, nx, ny)
}
}
board[x][y] = ch
}
for i, row := range board {
for j := range row {
dfs(t, i, j)
}
}
ans := make([]string, 0, len(seen))
for s := range seen {
ans = append(ans, s)
}
return ans
}
```
* [sol1-C++]
```C++
struct TrieNode {
string word;
unordered_map<char,TrieNode *> children;
TrieNode() {
this->word = "";
}
};
void insertTrie(TrieNode * root,const string & word) {
TrieNode * node = root;
for (auto c : word){
if (!node->children.count(c)) {
node->children[c] = new TrieNode();
}
node = node->children[c];
}
node->word = word;
}
class Solution {
public:
int dirs[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
bool dfs(vector<vector<char>>& board, int x, int y, TrieNode * root, set<string> & res) {
char ch = board[x][y];
if (!root->children.count(ch)) {
return false;
}
root = root->children[ch];
if (root->word.size() > 0) {
res.insert(root->word);
}
board[x][y] = '#';
for (int i = 0; i < 4; ++i) {
int nx = x + dirs[i][0];
int ny = y + dirs[i][1];
if (nx >= 0 && nx < board.size() && ny >= 0 && ny < board[0].size()) {
if (board[nx][ny] != '#') {
dfs(board, nx, ny, root,res);
}
}
}
board[x][y] = ch;
return true;
}
vector<string> findWords(vector<vector<char>> & board, vector<string> & words) {
TrieNode * root = new TrieNode();
set<string> res;
vector<string> ans;
for (auto & word: words){
insertTrie(root,word);
}
for (int i = 0; i < board.size(); ++i) {
for (int j = 0; j < board[0].size(); ++j) {
dfs(board, i, j, root, res);
}
}
for (auto & word: res) {
ans.emplace_back(word);
}
return ans;
}
};
```
**复杂度分析**
- 时间复杂度：$O(m \times n \times 3^{l-1})$，其中 $m$ 是二维网格的高度，$n$ 是二维网格的宽度，$l$ 是最长单词的长度。我们需要遍历 $m \times n$ 个单元格，每个单元格最多需要遍历 $4 \times 3^{l-1}$ 条路径。
- 空间复杂度：$O(k \times l)$，其中 $k$ 是 $\textit{words}$ 的长度，$l$ 是最长单词的长度。最坏情况下，我们需要 $O(k \times l)$ 用于存储前缀树。
#### 方法二：删除被匹配的单词
**思路和算法**
考虑以下情况。假设给定一个所有单元格都是 `a` 的二维字符网格和单词列表 `["a", "aa", "aaa", "aaaa"]` 。当我们使用方法一来找出所有同时在二维网格和单词列表中出现的单词时，我们需要遍历每一个单元格的所有路径，会找到大量重复的单词。
为了缓解这种情况，我们可以将匹配到的单词从前缀树中移除，来避免重复寻找相同的单词。因为这种方法可以保证每个单词只能被匹配一次；所以我们也不需要再对结果集去重了。
**代码**
* [sol2-Python3]
```Python
from collections import defaultdict
class Trie:
def __init__(self):
self.children = defaultdict(Trie)
self.word = ""
def insert(self, word):
cur = self
for c in word:
cur = cur.children[c]
cur.is_word = True
cur.word = word
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
trie = Trie()
for word in words:
trie.insert(word)
def dfs(now, i1, j1):
if board[i1][j1] not in now.children:
return
ch = board[i1][j1]
nxt = now.children[ch]
if nxt.word != "":
ans.append(nxt.word)
nxt.word = ""
if nxt.children:
board[i1][j1] = "#"
for i2, j2 in [(i1 + 1, j1), (i1 - 1, j1), (i1, j1 + 1), (i1, j1 - 1)]:
if 0 <= i2 < m and 0 <= j2 < n:
dfs(nxt, i2, j2)
board[i1][j1] = ch
if not nxt.children:
now.children.pop(ch)
ans = []
m, n = len(board), len(board[0])
for i in range(m):
for j in range(n):
dfs(trie, i, j)
return ans
```
* [sol2-Java]
```Java
class Solution {
int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
public List<String> findWords(char[][] board, String[] words) {
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
Set<String> ans = new HashSet<String>();
for (int i = 0; i < board.length; ++i) {
for (int j = 0; j < board[0].length; ++j) {
dfs(board, trie, i, j, ans);
}
}
return new ArrayList<String>(ans);
}
public void dfs(char[][] board, Trie now, int i1, int j1, Set<String> ans) {
if (!now.children.containsKey(board[i1][j1])) {
return;
}
char ch = board[i1][j1];
Trie nxt = now.children.get(ch);
if (!"".equals(nxt.word)) {
ans.add(nxt.word);
nxt.word = "";
}
if (!nxt.children.isEmpty()) {
board[i1][j1] = '#';
for (int[] dir : dirs) {
int i2 = i1 + dir[0], j2 = j1 + dir[1];
if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0].length) {
dfs(board, nxt, i2, j2, ans);
}
}
board[i1][j1] = ch;
}
if (nxt.children.isEmpty()) {
now.children.remove(ch);
}
}
}
class Trie {
String word;
Map<Character, Trie> children;
boolean isWord;
public Trie() {
this.word = "";
this.children = new HashMap<Character, Trie>();
}
public void insert(String word) {
Trie cur = this;
for (int i = 0; i < word.length(); ++i) {
char c = word.charAt(i);
if (!cur.children.containsKey(c)) {
cur.children.put(c, new Trie());
}
cur = cur.children.get(c);
}
cur.word = word;
}
}
```
* [sol2-C#]
```C#
public class Solution {
int[][] dirs = new int[][] {
new int[]{1, 0},
new int[]{-1, 0},
new int[]{0, 1},
new int[]{0, -1}
};
public IList<string> FindWords(char[][] board, string[] words) {
Trie trie = new Trie();
foreach (string word in words) {
trie.Insert(word);
}
ISet<string> ans = new HashSet<string>();
for (int i = 0; i < board.Length; ++i) {
for (int j = 0; j < board[0].Length; ++j) {
DFS(board, trie, i, j, ans);
}
}
return new List<string>(ans);
}
void DFS(char[][] board, Trie now, int i1, int j1, ISet<string> ans) {
if (!now.children.ContainsKey(board[i1][j1])) {
return;
}
char ch = board[i1][j1];
Trie nxt = now.children[ch];
if (!"".Equals(nxt.word)) {
ans.Add(nxt.word);
nxt.word = "";
}
if (nxt.children.Count > 0) {
board[i1][j1] = '#';
int[][] dirs = new int[][] {
new int[]{1, 0},
new int[]{-1, 0},
new int[]{0, 1},
new int[]{0, -1}
};
foreach (int[] dir in dirs) {
int i2 = i1 + dir[0], j2 = j1 + dir[1];
if (i2 >= 0 && i2 < board.Length && j2 >= 0 && j2 < board[0].Length) {
DFS(board, nxt, i2, j2, ans);
}
}
board[i1][j1] = ch;
}
if (nxt.children.Count == 0) {
now.children.Remove(ch);
}
}
}
class Trie {
public string word;
public Dictionary<char, Trie> children;
public bool isWord;
public Trie() {
this.word = "";
this.children = new Dictionary<char, Trie>();
}
public void Insert(string word) {
Trie cur = this;
foreach (char c in word) {
if (!cur.children.ContainsKey(c)) {
cur.children.Add(c, new Trie());
}
cur = cur.children[c];
}
cur.word = word;
}
}
```
* [sol2-Golang]
```go
type Trie struct {
children map[byte]*Trie
word string
}
func (t *Trie) Insert(word string) {
node := t
for i := range word {
ch := word[i]
if node.children[ch] == nil {
node.children[ch] = &Trie{children: map[byte]*Trie{}}
}
node = node.children[ch]
}
node.word = word
}
var dirs = []struct{ x, y int }{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
func findWords(board [][]byte, words []string) (ans []string) {
t := &Trie{children: map[byte]*Trie{}}
for _, word := range words {
t.Insert(word)
}
m, n := len(board), len(board[0])
var dfs func(node *Trie, x, y int)
dfs = func(node *Trie, x, y int) {
ch := board[x][y]
nxt := node.children[ch]
if nxt == nil {
return
}
if nxt.word != "" {
ans = append(ans, nxt.word)
nxt.word = ""
}
if len(nxt.children) > 0 {
board[x][y] = '#'
for _, d := range dirs {
nx, ny := x+d.x, y+d.y
if 0 <= nx && nx < m && 0 <= ny && ny < n && board[nx][ny] != '#' {
dfs(nxt, nx, ny)
}
}
board[x][y] = ch
}
if len(nxt.children) == 0 {
delete(node.children, ch)
}
}
for i, row := range board {
for j := range row {
dfs(t, i, j)
}
}
return
}
```
* [sol2-C++]
```C++
struct TrieNode {
string word;
unordered_map<char, TrieNode *> children;
TrieNode() {
this->word = "";
}
};
void insertTrie(TrieNode * root, const string & word) {
TrieNode * node = root;
for (auto c : word) {
if (!node->children.count(c)) {
node->children[c] = new TrieNode();
}
node = node->children[c];
}
node->word = word;
}
class Solution {
public:
int dirs[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
bool dfs(vector<vector<char>>& board, int x, int y, TrieNode * root, set<string> & res) {
char ch = board[x][y];
if (!root->children.count(ch)) {
return false;
}
root = root->children[ch];
if (root->word.size() > 0 ) {
res.insert(root->word);
root->word = "";
}
board[x][y] = '#';
for (int i = 0; i < 4; ++i) {
int nx = x + dirs[i][0];
int ny = y + dirs[i][1];
if (nx >= 0 && nx < board.size() && ny >= 0 && ny < board[0].size()) {
if (board[nx][ny] != '#'){
dfs(board, nx, ny, root,res);
}
}
}
board[x][y] = ch;
return true;
}
vector<string> findWords(vector<vector<char>> & board, vector<string> & words) {
TrieNode * root = new TrieNode();
set<string> res;
vector<string> ans;
for (auto & word: words) {
insertTrie(root,word);
}
for (int i = 0; i < board.size(); ++i) {
for(int j = 0; j < board[0].size(); ++j) {
dfs(board, i, j, root, res);
}
}
for (auto & word: res) {
ans.emplace_back(word);
}
return ans;
}
};
```
**复杂度分析**
- 时间复杂度：$O(m \times n \times 3^{l-1})$，其中 $m$ 是二维网格的高度，$n$ 是二维网格的宽度，$l$ 是最长单词的长度。我们仍需要遍历 $m \times n$ 个单元格，每个单元格在最坏情况下仍需要遍历 $4 \times 3^{l-1}$ 条路径。
- 空间复杂度：$O(k \times l)$，其中 $k$ 是 $\textit{words}$ 的长度，$l$ 是最长单词的长度。最坏情况下，我们需要 $O(k \times l)$ 用于存储前缀树。

139
src/main/java/leetcode/editor/cn/doc/solution/fan-zhuan-ju-zhen-hou-de-de-fen-by-leetc-cxma.lcv Normal file
View File

@ -0,0 +1,139 @@
#### 方法一：贪心
根据题意，能够知道一个重要的事实：给定一个翻转方案，则它们之间任意交换顺序后，得到的结果保持不变。因此，我们总可以先考虑所有的行翻转，再考虑所有的列翻转。
不难发现一点：为了得到最高的分数，矩阵的每一行的最左边的数都必须为 $1$。为了做到这一点，我们可以翻转那些最左边的数不为 $1$ 的那些行，而其他的行则保持不动。
当将每一行的最左边的数都变为 $1$ 之后，就只能进行列翻转了。为了使得总得分最大，我们要让每个列中 $1$ 的数目尽可能多。因此，我们扫描除了最左边的列以外的每一列，如果该列 $0$ 的数目多于 $1$ 的数目，就翻转该列，其他的列则保持不变。
实际编写代码时，我们无需修改原矩阵，而是可以计算每一列对总分数的「贡献」，从而直接计算出最高的分数。假设矩阵共有 $m$ 行 $n$ 列，计算方法如下：
- 对于最左边的列而言，由于最优情况下，它们的取值都为 $1$，因此每个元素对分数的贡献都为 $2^{n-1}$，总贡献为 $m \times 2^{n-1}$。
- 对于第 $j$ 列（$j>0$，此处规定最左边的列是第 $0$ 列）而言，我们统计这一列 $0,1$ 的数量，令其中的最大值为 $k$，则 $k$ 是列翻转后的 $1$ 的数量，该列的总贡献为 $k \times 2^{n-j-1}$。需要注意的是，在统计 $0,1$ 的数量的时候，**要考虑最初进行的行反转**。
* [sol1-C++]
```C++
class Solution {
public:
int matrixScore(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int ret = m * (1 << (n - 1));
for (int j = 1; j < n; j++) {
int nOnes = 0;
for (int i = 0; i < m; i++) {
if (grid[i][0] == 1) {
nOnes += grid[i][j];
} else {
nOnes += (1 - grid[i][j]); // 如果这一行进行了行反转，则该元素的实际取值为 1 - grid[i][j]
}
}
int k = max(nOnes, m - nOnes);
ret += k * (1 << (n - j - 1));
}
return ret;
}
};
```
* [sol1-Java]
```Java
class Solution {
public int matrixScore(int[][] grid) {
int m = grid.length, n = grid[0].length;
int ret = m * (1 << (n - 1));
for (int j = 1; j < n; j++) {
int nOnes = 0;
for (int i = 0; i < m; i++) {
if (grid[i][0] == 1) {
nOnes += grid[i][j];
} else {
nOnes += (1 - grid[i][j]); // 如果这一行进行了行反转，则该元素的实际取值为 1 - grid[i][j]
}
}
int k = Math.max(nOnes, m - nOnes);
ret += k * (1 << (n - j - 1));
}
return ret;
}
}
```
* [sol1-Golang]
```Golang
func matrixScore(grid [][]int) int {
m, n := len(grid), len(grid[0])
ans := 1 << (n - 1) * m
for j := 1; j < n; j++ {
ones := 0
for _, row := range grid {
if row[j] == row[0] {
ones++
}
}
if ones < m-ones {
ones = m - ones
}
ans += 1 << (n - 1 - j) * ones
}
return ans
}
```
* [sol1-JavaScript]
```JavaScript
var matrixScore = function(grid) {
const m = grid.length, n = grid[0].length;
let ret = m * (1 << (n - 1));
for (let j = 1; j < n; j++) {
let nOnes = 0;
for (let i = 0; i < m; i++) {
if (grid[i][0] === 1) {
nOnes += grid[i][j];
} else {
nOnes += (1 - grid[i][j]); // 如果这一行进行了行反转，则该元素的实际取值为 1 - grid[i][j]
}
}
const k = Math.max(nOnes, m - nOnes);
ret += k * (1 << (n - j - 1));
}
return ret;
};
```
* [sol1-C]
```C
int matrixScore(int** grid, int gridSize, int* gridColSize) {
int m = gridSize, n = gridColSize[0];
int ret = m * (1 << (n - 1));
for (int j = 1; j < n; j++) {
int nOnes = 0;
for (int i = 0; i < m; i++) {
if (grid[i][0] == 1) {
nOnes += grid[i][j];
} else {
nOnes += (1 - grid[i][j]); // 如果这一行进行了行反转，则该元素的实际取值为 1 - grid[i][j]
}
}
int k = fmax(nOnes, m - nOnes);
ret += k * (1 << (n - j - 1));
}
return ret;
}
```
**复杂度分析**
- 时间复杂度：$O(mn)$，其中 $m$ 为矩阵行数，$n$ 为矩阵列数。
- 空间复杂度：$O(1)$。

426
src/main/java/leetcode/editor/cn/doc/solution/fei-bo-na-qi-shu-lie-by-leetcode-solutio-hbss.lcv Normal file
View File

@ -0,0 +1,426 @@
#### 方法一：动态规划
斐波那契数的边界条件是 $F(0)=0$ 和 $F(1)=1$。当 $n>1$ 时，每一项的和都等于前两项的和，因此有如下递推关系：
$F(n)=F(n-1)+F(n-2)$
由于斐波那契数存在递推关系，因此可以使用动态规划求解。动态规划的状态转移方程即为上述递推关系，边界条件为 $F(0)$ 和 $F(1)$。
根据状态转移方程和边界条件，可以得到时间复杂度和空间复杂度都是 $O(n)$ 的实现。由于 $F(n)$ 只和 $F(n-1)$ 与 $F(n-2)$ 有关，因此可以使用「滚动数组思想」把空间复杂度优化成 $O(1)$。**如下的代码中给出的就是这种实现。**
计算过程中，答案需要取模 $1\text{e}9+7$。
![fig1](https://assets.leetcode-cn.com/solution-static/jianzhi_10_I/10_I_fig1.gif)
* [sol1-Java]
```Java
class Solution {
public int fib(int n) {
final int MOD = 1000000007;
if (n < 2) {
return n;
}
int p = 0, q = 0, r = 1;
for (int i = 2; i <= n; ++i) {
p = q;
q = r;
r = (p + q) % MOD;
}
return r;
}
}
```
* [sol1-C#]
```C#
public class Solution {
public int Fib(int n) {
const int MOD = 1000000007;
if (n < 2) {
return n;
}
int p = 0, q = 0, r = 1;
for (int i = 2; i <= n; ++i) {
p = q;
q = r;
r = (p + q) % MOD;
}
return r;
}
}
```
* [sol1-C++]
```C++
class Solution {
public:
int fib(int n) {
int MOD = 1000000007;
if (n < 2) {
return n;
}
int p = 0, q = 0, r = 1;
for (int i = 2; i <= n; ++i) {
p = q;
q = r;
r = (p + q)%MOD;
}
return r;
}
};
```
* [sol1-JavaScript]
```JavaScript
var fib = function(n) {
const MOD = 1000000007;
if (n < 2) {
return n;
}
let p = 0, q = 0, r = 1;
for (let i = 2; i <= n; ++i) {
p = q;
q = r;
r = (p + q) % MOD;
}
return r;
};
```
* [sol1-Golang]
```go
func fib(n int) int {
const mod int = 1e9 + 7
if n < 2 {
return n
}
p, q, r := 0, 0, 1
for i := 2; i <= n; i++ {
p = q
q = r
r = (p + q) % mod
}
return r
}
```
* [sol1-Python3]
```Python
class Solution:
def fib(self, n: int) -> int:
MOD = 10 ** 9 + 7
if n < 2:
return n
p, q, r = 0, 0, 1
for i in range(2, n + 1):
p = q
q = r
r = (p + q) % MOD
return r
```
**复杂度分析**
- 时间复杂度：$O(n)$。
- 空间复杂度：$O(1)$。
#### 方法二：矩阵快速幂
方法一的时间复杂度是 $O(n)$。使用矩阵快速幂的方法可以降低时间复杂度。
首先我们可以构建这样一个递推关系：
$$
\left[
\begin{matrix}
1 & 1 \\
1 & 0
\end{matrix}
\right]
\left[
\begin{matrix}
F(n)\\
F(n - 1)
\end{matrix}
\right] =
\left[
\begin{matrix}
F(n) + F(n - 1)\\
F(n)
\end{matrix}
\right] =
\left[
\begin{matrix}
F(n + 1)\\
F(n)
\end{matrix}
\right]
$$
因此：
$$
\left[
\begin{matrix}
F(n + 1)\\
F(n)
\end{matrix}
\right] =
\left[
\begin{matrix}
1 & 1 \\
1 & 0
\end{matrix}
\right] ^n
\left[
\begin{matrix}
F(1)\\
F(0)
\end{matrix}
\right]
$$
令：
$$
M = \left[
\begin{matrix}
1 & 1 \\
1 & 0
\end{matrix}
\right]
$$
因此只要我们能快速计算矩阵 $M$ 的 $n$ 次幂，就可以得到 $F(n)$ 的值。如果直接求取 $M^n$，时间复杂度是 $O(n)$，可以定义矩阵乘法，然后用快速幂算法来加速这里 $M^n$ 的求取。
计算过程中，答案需要取模 $1\text{e}9+7$。
* [sol2-Java]
```Java
class Solution {
static final int MOD = 1000000007;
public int fib(int n) {
if (n < 2) {
return n;
}
int[][] q = {{1, 1}, {1, 0}};
int[][] res = pow(q, n - 1);
return res[0][0];
}
public int[][] pow(int[][] a, int n) {
int[][] ret = {{1, 0}, {0, 1}};
while (n > 0) {
if ((n & 1) == 1) {
ret = multiply(ret, a);
}
n >>= 1;
a = multiply(a, a);
}
return ret;
}
public int[][] multiply(int[][] a, int[][] b) {
int[][] c = new int[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
}
}
return c;
}
}
```
* [sol2-C#]
```C#
public class Solution {
const int MOD = 1000000007;
public int Fib(int n) {
if (n < 2) {
return n;
}
int[,] q = {{1, 1}, {1, 0}};
int[,] res = Pow(q, n - 1);
return res[0, 0];
}
public int[,] Pow(int[,] a, int n) {
int[,] ret = {{1, 0}, {0, 1}};
while (n > 0) {
if ((n & 1) == 1) {
ret = Multiply(ret, a);
}
n >>= 1;
a = Multiply(a, a);
}
return ret;
}
public int[,] Multiply(int[,] a, int[,] b) {
int[,] c = new int[2, 2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i, j] = (int) (((long) a[i, 0] * b[0, j] + (long) a[i, 1] * b[1, j]) % MOD);
}
}
return c;
}
}
```
* [sol2-C++]
```C++
class Solution {
public:
const int MOD = 1000000007;
int fib(int n) {
if (n < 2) {
return n;
}
vector<vector<long>> q{{1, 1}, {1, 0}};
vector<vector<long>> res = pow(q, n - 1);
return res[0][0];
}
vector<vector<long>> pow(vector<vector<long>>& a, int n) {
vector<vector<long>> ret{{1, 0}, {0, 1}};
while (n > 0) {
if (n & 1) {
ret = multiply(ret, a);
}
n >>= 1;
a = multiply(a, a);
}
return ret;
}
vector<vector<long>> multiply(vector<vector<long>>& a, vector<vector<long>>& b) {
vector<vector<long>> c{{0, 0}, {0, 0}};
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD;
}
}
return c;
}
};
```
* [sol2-JavaScript]
```JavaScript
var fib = function(n) {
if (n < 2) {
return n;
}
const q = [[1, 1], [1, 0]];
const res = pow(q, n - 1);
return res[0][0];
};
const pow = (a, n) => {
let ret = [[1, 0], [0, 1]];
while (n > 0) {
if ((n & 1) === 1) {
ret = multiply(ret, a);
}
n >>= 1;
a = multiply(a, a);
}
return ret;
}
const multiply = (a, b) => {
const c = new Array(2).fill(0).map(() => new Array(2).fill(0));
for (let i = 0; i < 2; i++) {
for (let j = 0; j < 2; j++) {
c[i][j] = (BigInt(a[i][0]) * BigInt(b[0][j]) + BigInt(a[i][1]) * BigInt(b[1][j])) % BigInt(1000000007);
}
}
return c;
}
```
* [sol2-Golang]
```go
const mod int = 1e9 + 7
type matrix [2][2]int
func multiply(a, b matrix) (c matrix) {
for i := 0; i < 2; i++ {
for j := 0; j < 2; j++ {
c[i][j] = (a[i][0]*b[0][j] + a[i][1]*b[1][j]) % mod
}
}
return
}
func pow(a matrix, n int) matrix {
ret := matrix{{1, 0}, {0, 1}}
for ; n > 0; n >>= 1 {
if n&1 == 1 {
ret = multiply(ret, a)
}
a = multiply(a, a)
}
return ret
}
func fib(n int) int {
if n < 2 {
return n
}
res := pow(matrix{{1, 1}, {1, 0}}, n-1)
return res[0][0]
}
```
* [sol2-Python3]
```Python
class Solution:
def fib(self, n: int) -> int:
MOD = 10 ** 9 + 7
if n < 2:
return n
def multiply(a: List[List[int]], b: List[List[int]]) -> List[List[int]]:
c = [[0, 0], [0, 0]]
for i in range(2):
for j in range(2):
c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD
return c
def matrix_pow(a: List[List[int]], n: int) -> List[List[int]]:
ret = [[1, 0], [0, 1]]
while n > 0:
if n & 1:
ret = multiply(ret, a)
n >>= 1
a = multiply(a, a)
return ret
res = matrix_pow([[1, 1], [1, 0]], n - 1)
return res[0][0]
```
**复杂度分析**
- 时间复杂度：$O(\log n)$。
- 空间复杂度：$O(1)$。

288
src/main/java/leetcode/editor/cn/doc/solution/gei-biao-da-shi-tian-jia-yun-suan-fu-by-2o1s7.lcv Normal file
View File

@ -0,0 +1,288 @@
#### 方法一：回溯
设字符串 $\textit{num}$ 的长度为 $n$，为构建表达式，我们可以往 $\textit{num}$ 中间的 $n-1$ 个空隙添加 $\texttt{+}$ 号、$\texttt{-}$ 号或 $\texttt{*}$ 号，或者不添加符号。
我们可以用「回溯法」来模拟这个过程。从左向右构建表达式，并实时计算表达式的结果。由于乘法运算优先级高于加法和减法运算，我们还需要保存最后一个连乘串（如 $\texttt{2*3*4}$）的运算结果。
定义递归函数 $\textit{backtrack}(\textit{expr}, i, \textit{res}, \textit{mul})$，其中：
- $\textit{expr}$ 为当前构建出的表达式；
- $i$ 表示当前的枚举到了 $\textit{num}$ 的第 $i$ 个数字；
- $\textit{res}$ 为当前表达式的计算结果；
- $\textit{mul}$ 为表达式最后一个连乘串的计算结果。
该递归函数分为两种情况：
- 如果 $i=n$，说明表达式已经构造完成，若此时有 $\textit{res}=\textit{target}$，则找到了一个可行解，我们将 $\textit{expr}$ 放入答案数组中，递归结束；
- 如果 $i<n$，需要枚举当前表达式末尾要添加的符号（$\texttt{+}$ 号、$\texttt{-}$ 号或 $\texttt{*}$ 号），以及该符号之后需要截取多少位数字。设该符号之后的数字为 $\textit{val}$，按符号分类讨论：
- 若添加 $\texttt{+}$ 号，则 $\textit{res}$ 增加 $\textit{val}$，且 $\textit{val}$ 单独组成表达式最后一个连乘串；
- 若添加 $\texttt{-}$ 号，则 $\textit{res}$ 减少 $\textit{val}$，且 $-\textit{val}$ 单独组成表达式最后一个连乘串；
- 若添加 $\texttt{*}$ 号，由于乘法运算优先级高于加法和减法运算，我们需要对 $\textit{res}$ 撤销之前 $\textit{mul}$ 的计算结果，并添加新的连乘结果 $\textit{mul}*\textit{val}$，也就是将 $\textit{res}$ 减少 $\textit{mul}$ 并增加 $\textit{mul}*\textit{val}$。
代码实现时，为避免字符串拼接所带来的额外时间开销，我们采用字符数组的形式来构建表达式。此外，运算过程中可能会产生超过 $32$ 位整数的结果，我们要用 $64$ 位整数存储中间运算结果。
* [sol1-Python3]
```Python
class Solution:
def addOperators(self, num: str, target: int) -> List[str]:
n = len(num)
ans = []
def backtrack(expr: List[str], i: int, res: int, mul: int):
if i == n:
if res == target:
ans.append(''.join(expr))
return
signIndex = len(expr)
if i > 0:
expr.append('') # 占位，下面填充符号
val = 0
for j in range(i, n): # 枚举截取的数字长度（取多少位）
if j > i and num[i] == '0': # 数字可以是单个 0 但不能有前导零
break
val = val * 10 + int(num[j])
expr.append(num[j])
if i == 0: # 表达式开头不能添加符号
backtrack(expr, j + 1, val, val)
else: # 枚举符号
expr[signIndex] = '+'; backtrack(expr, j + 1, res + val, val)
expr[signIndex] = '-'; backtrack(expr, j + 1, res - val, -val)
expr[signIndex] = '*'; backtrack(expr, j + 1, res - mul + mul * val, mul * val)
del expr[signIndex:]
backtrack([], 0, 0, 0)
return ans
```
* [sol1-C++]
```C++
class Solution {
public:
vector<string> addOperators(string num, int target) {
int n = num.length();
vector<string> ans;
function<void(string&, int, long, long)> backtrack = [&](string &expr, int i, long res, long mul) {
if (i == n) {
if (res == target) {
ans.emplace_back(expr);
}
return;
}
int signIndex = expr.size();
if (i > 0) {
expr.push_back(0); // 占位，下面填充符号
}
long val = 0;
// 枚举截取的数字长度（取多少位），注意数字可以是单个 0 但不能有前导零
for (int j = i; j < n && (j == i || num[i] != '0'); ++j) {
val = val * 10 + num[j] - '0';
expr.push_back(num[j]);
if (i == 0) { // 表达式开头不能添加符号
backtrack(expr, j + 1, val, val);
} else { // 枚举符号
expr[signIndex] = '+'; backtrack(expr, j + 1, res + val, val);
expr[signIndex] = '-'; backtrack(expr, j + 1, res - val, -val);
expr[signIndex] = '*'; backtrack(expr, j + 1, res - mul + mul * val, mul * val);
}
}
expr.resize(signIndex);
};
string expr;
backtrack(expr, 0, 0, 0);
return ans;
}
};
```
* [sol1-Java]
```Java
class Solution {
int n;
String num;
int target;
List<String> ans;
public List<String> addOperators(String num, int target) {
this.n = num.length();
this.num = num;
this.target = target;
this.ans = new ArrayList<String>();
StringBuffer expr = new StringBuffer();
backtrack(expr, 0, 0, 0);
return ans;
}
public void backtrack(StringBuffer expr, int i, long res, long mul) {
if (i == n) {
if (res == target) {
ans.add(expr.toString());
}
return;
}
int signIndex = expr.length();
if (i > 0) {
expr.append(0); // 占位，下面填充符号
}
long val = 0;
// 枚举截取的数字长度（取多少位），注意数字可以是单个 0 但不能有前导零
for (int j = i; j < n && (j == i || num.charAt(i) != '0'); ++j) {
val = val * 10 + num.charAt(j) - '0';
expr.append(num.charAt(j));
if (i == 0) { // 表达式开头不能添加符号
backtrack(expr, j + 1, val, val);
} else { // 枚举符号
expr.setCharAt(signIndex, '+');
backtrack(expr, j + 1, res + val, val);
expr.setCharAt(signIndex, '-');
backtrack(expr, j + 1, res - val, -val);
expr.setCharAt(signIndex, '*');
backtrack(expr, j + 1, res - mul + mul * val, mul * val);
}
}
expr.setLength(signIndex);
}
}
```
* [sol1-C#]
```C#
public class Solution {
int n;
string num;
int target;
IList<string> ans;
public IList<string> AddOperators(string num, int target) {
this.n = num.Length;
this.num = num;
this.target = target;
this.ans = new List<string>();
StringBuilder expr = new StringBuilder();
Backtrack(expr, 0, 0, 0);
return ans;
}
public void Backtrack(StringBuilder expr, int i, long res, long mul) {
if (i == n) {
if (res == target) {
ans.Add(expr.ToString());
}
return;
}
int signIndex = expr.Length;
if (i > 0) {
expr.Append(0); // 占位，下面填充符号
}
long val = 0;
// 枚举截取的数字长度（取多少位），注意数字可以是单个 0 但不能有前导零
for (int j = i; j < n && (j == i || num[i] != '0'); ++j) {
val = val * 10 + num[j] - '0';
expr.Append(num[j]);
if (i == 0) { // 表达式开头不能添加符号
Backtrack(expr, j + 1, val, val);
} else { // 枚举符号
expr.Replace(expr[signIndex], '+', signIndex, 1);
Backtrack(expr, j + 1, res + val, val);
expr.Replace(expr[signIndex], '-', signIndex, 1);
Backtrack(expr, j + 1, res - val, -val);
expr.Replace(expr[signIndex], '*', signIndex, 1);
Backtrack(expr, j + 1, res - mul + mul * val, mul * val);
}
}
expr.Length = signIndex;
}
}
```
* [sol1-Golang]
```go
func addOperators(num string, target int) (ans []string) {
n := len(num)
var backtrack func(expr []byte, i, res, mul int)
backtrack = func(expr []byte, i, res, mul int) {
if i == n {
if res == target {
ans = append(ans, string(expr))
}
return
}
signIndex := len(expr)
if i > 0 {
expr = append(expr, 0) // 占位，下面填充符号
}
// 枚举截取的数字长度（取多少位），注意数字可以是单个 0 但不能有前导零
for j, val := i, 0; j < n && (j == i || num[i] != '0'); j++ {
val = val*10 + int(num[j]-'0')
expr = append(expr, num[j])
if i == 0 { // 表达式开头不能添加符号
backtrack(expr, j+1, val, val)
} else { // 枚举符号
expr[signIndex] = '+'; backtrack(expr, j+1, res+val, val)
expr[signIndex] = '-'; backtrack(expr, j+1, res-val, -val)
expr[signIndex] = '*'; backtrack(expr, j+1, res-mul+mul*val, mul*val)
}
}
}
backtrack(make([]byte, 0, n*2-1), 0, 0, 0)
return
}
```
* [sol1-JavaScript]
```JavaScript
var addOperators = function(num, target) {
const n = num.length;
const ans = [];
let expr = [];
const backtrack = (expr, i, res, mul) => {
if (i === n) {
if (res === target) {
ans.push(expr.join(''));
}
return;
}
const signIndex = expr.length;
if (i > 0) {
expr.push(''); // 占位，下面填充符号
}
let val = 0;
// 枚举截取的数字长度（取多少位），注意数字可以是单个 0 但不能有前导零
for (let j = i; j < n && (j === i || num[i] !== '0'); ++j) {
val = val * 10 + num[j].charCodeAt() - '0'.charCodeAt();
expr.push(num[j]);
if (i === 0) { // 表达式开头不能添加符号
backtrack(expr, j + 1, val, val);
} else { // 枚举符号
expr[signIndex] = '+';
backtrack(expr, j + 1, res + val, val);
expr[signIndex] = '-';
backtrack(expr, j + 1, res - val, -val);
expr[signIndex] = '*';
backtrack(expr, j + 1, res - mul + mul * val, mul * val);
}
}
expr = expr.splice(signIndex, expr.length - signIndex)
}
backtrack(expr, 0, 0, 0);
return ans;
}
```
**复杂度分析**
- 时间复杂度：$O(4^n)$，其中 $n$ 是字符串 $\textit{num}$ 的长度。由于在数字之间可以选择不添加符号、添加 $\texttt{+}$ 号、$\texttt{-}$ 号或 $\texttt{*}$ 号，一共有 $4$ 种选择，因此时间复杂度为 $O(4^n)$。
注：考虑到将 $\textit{expr}$ 的拷贝存入答案需要花费 $O(n)$ 的时间，最终的时间复杂度似乎是 $O(n \times 4^n)$。果真如此吗？考虑合法表达式最多的情况，即 $\textit{num}$ 全为 $\texttt{0}$，且 $\textit{target}=0$ 的情况，由于不能有前导零，我们必须在数字之间添加 $\texttt{+ - *}$ 三者之一，所以合法表达式有 $3^{n-1}$ 个，因此「将 $\textit{expr}$ 的拷贝存入答案」这一部分的时间开销至多为 $O(n \times 3^n)$。
- 空间复杂度：$O(n)$。不考虑返回值的空间占用，空间复杂度取决于递归时的栈空间。

87
src/main/java/leetcode/editor/cn/doc/solution/gong-shui-san-xie-k-jin-zhi-zhu-wei-shen-zmd4.lcv Normal file
View File

@ -0,0 +1,87 @@
## 基本分析
给定一个随机生成 $1$ ~ $7$ 的函数，要求实现等概率返回 $1$ ~ $10$ 的函数。
首先需要知道，在输出域上进行定量整体偏移，仍然满足等概率，即要实现 $0$ ~ $6$ 随机器，只需要在 `rand7` 的返回值上进行 $-1$ 操作即可。
但输出域的 拼接/叠加 并不满足等概率。例如 `rand7() + rand7()` 会产生 $[2, 14]$ 范围内的数，但每个数并非等概率：
* 产生 $2$ 的概率为：$\frac{1}{7} * \frac{1}{7} = \frac{1}{49}$
* 产生 $4$ 的概率为：$\frac{1}{7} * \frac{1}{7} + \frac{1}{7} * \frac{1}{7} + \frac{1}{7} * \frac{1}{7} = \frac{3}{49}$
在 $[2, 14]$ 这 $13$ 个数里面，等概率的数值不足 $10$ 个。
**因此，你应该知道「执行两次 `rand7()` 相加，将 $[1, 10]$ 范围内的数进行返回，否则一直重试」的做法是错误的。**
---
## $k$ 进制诸位生成 + 拒绝采样
上述做法出现概率分布不均的情况，是因为两次随机值的不同组合「相加」的会出现相同的结果（$(1, 3)$、$(2, 2)$、$(3, 1)$ 最终结果均为 $4$）。
结合每次执行 `rand7` 都可以看作一次独立事件。我们可以将两次 `rand7` 的结果看作生成 $7$ 进制的两位。**从而实现每个数值都唯一对应了一种随机值的组合（等概率），反之亦然。**
举个🌰，设随机执行两次 `rand7` 得到的结果分别是 $4$（第一次）、$7$（第二次），由于我们是要 $7$ 进制的数，因此可以先对 `rand7` 的执行结果进行 $-1$ 操作，将输出域偏移到 $[0, 6]$（仍为等概率），即得到 $3$（第一次）和 $6$（第二次），最终得到的是数值 $(63)_7$，数值 $(63)_7$ 唯一对应了我们的随机值组合方案，反过来随机值组合方案也唯一对应一个 $7$ 进制的数值。
**那么根据「进制转换」的相关知识，如果我们存在一个 `randK` 的函数，对其执行 $n$ 次，我们能够等概率产生 $[0, K^n - 1]$ 范围内的数值。**
回到本题，执行一次 `rand7` 只能产生 $[0, 6]$ 范围内的数值，不足 $10$ 个；而执行 $2$ 次 `rand7` 的话则能产生 $[0, 48]$ 范围内的数值，足够 $10$ 个，且等概率。
我们只需要判定生成的值是否为题意的 $[1, 10]$ 即可，如果是的话直接返回，否则一直重试。
代码：
* []
```Java
class Solution extends SolBase {
public int rand10() {
while (true) {
int ans = (rand7() - 1) * 7 + (rand7() - 1); // 进制转换
if (1 <= ans && ans <= 10) return ans;
}
}
}
```
* 时间复杂度：期望复杂度为 $O(1)$，最坏情况下为 $O(\infty)$
* 空间复杂度：$O(1)$
---
## 进阶
1. 降低对 `rand7` 的调用次数
我们发现，在上述解法中，范围 $[0, 48]$ 中，只有 $[1, 10]$ 范围内的数据会被接受返回，其余情况均被拒绝重试。
为了尽可能少的调用 `rand7` 方法，我们可以从 $[0, 48]$ 中取与 $[1, 10]$ 成倍数关系的数，来进行转换。
我们可以取 $[0, 48]$ 中的 $[1, 40]$ 范围内的数来代指 $[1, 10]$。
首先在 $[0, 48]$ 中取 $[1, 40]$ 仍为等概率，其次形如 $x1$ 的数值有 $4$ 个（$1$、$11$、$21$、$31$），形如 $x2$ 的数值有 $4$ 个（$2$、$12$、$22$、$32$）... 因此最终结果仍为等概率。
代码：
* []
```Java
class Solution extends SolBase {
public int rand10() {
while (true) {
int ans = (rand7() - 1) * 7 + (rand7() - 1); // 进制转换
if (1 <= ans && ans <= 40) return ans % 10 + 1;
}
}
}
```
* 时间复杂度：期望复杂度为 $O(1)$，最坏情况下为 $O(\infty)$
* 空间复杂度：$O(1)$
2. 计算 `rand7` 的期望调用次数
在 $[0, 48]$ 中我们采纳了 $[1, 40]$ 范围内的数值，即以调用两次为基本单位的话，有 $\frac{40}{49}$ 的概率被接受返回（成功）。
成功的概率为 $\frac{40}{49}$，那么触发成功所需次数（期望次数）为其倒数 $\frac{49}{40} = 1.225$，每次会调用两次 `rand7`，因而总的期望调用次数为 $1.225 * 2 = 2.45$ 。

56
src/main/java/leetcode/editor/cn/doc/solution/jian-dan-tan-xin-shou-ba-shou-jiao-xue-k-a0mp.lcv Normal file
View File

@ -0,0 +1,56 @@
### 题目描述
找到不大于 n 的最大的数，该数满足从高位到低位的数字非严格递增。
### 思路解析
这是一道很明显的贪心题目。既然要尽可能的大，那么这个数从高位开始要尽可能地保持不变。那么我们找到从高到低第一个满足 $str[i] > str[i+1]$ 的位置，然后把 $str[i] - 1$ ，再把后面的位置都变成 $9$ 即可。对应可看下面的例子。
*
```
n = 1234321
res = 1233999
```
但是由于减小了 $str[i]$ 以后，可能不满足 $str[i-1] <= str[i]$ 了，所以我们在分析下这种情况怎么处理。我们看下这种情况的例子：
*
```
n = 2333332
res = 2299999
```
下面这段比较啰嗦，其实你看了上面的例子你就知道怎么写了。
注意到如果减小 $str[i]$ 以后不满足 $str[i-1] <= str[i]$，那么肯定有 $str[i-1] == str[i]$，此时就需要再 $str[i-1] - 1$，递归地会处理到某个位置 $idx$，我们发现 $str[idx] == str[idx + 1] == ... = str[i]$ 。然后只要$str[idx] - 1$，然后后面都补上 $9$ 即可。
所以代码写起来很简单了。遍历各位数字的时候，求当前最大的数字 max。然后只在 $max < arr[i]$ 的时候才更新 max 对应的 idx（写法类似于查找数组中最大的元素，返回最小的下标）。接着判断是否有 $arr[i] > arr[i + 1]$，如果是，那么 idx 位置数字减 $1$，后面的位置全部置 $9$ 即可。
* []
```Java
class Solution {
public int monotoneIncreasingDigits(int N) {
char[] arr = (N + "").toCharArray();
int max = -1, idx = -1;
for (int i = 0; i < arr.length - 1; i++) {
if (max < arr[i]) {
max = arr[i];
idx = i;
}
if (arr[i] > arr[i + 1]) {
arr[idx] -= 1;
for(int j = idx + 1;j < arr.length;j++) {
arr[j] = '9';
}
break;
}
}
return Integer.parseInt(new String(arr));
}
}
```
时间复杂度：$O(\log N)$。数字为 $N$，位数为 $\log N$。遍历一遍即可出结果。
空间复杂度：$O(\log N)$。用于存储 char 数组。

392
src/main/java/leetcode/editor/cn/doc/solution/lu-jing-zong-he-iii-by-leetcode-solution-z9td.lcv Normal file
View File

@ -0,0 +1,392 @@
#### 方法一：深度优先搜索
**思路与算法**
我们首先想到的解法是穷举所有的可能，我们访问每一个节点 $\textit{node}$，检测以 $\textit{node}$ 为起始节点且向下延深的路径有多少种。我们递归遍历每一个节点的所有可能的路径，然后将这些路径数目加起来即为返回结果。
+ 我们首先定义 $\textit{rootSum}(p,\textit{val})$ 表示以节点 $p$ 为起点向下且满足路径总和为 $val$ 的路径数目。我们对二叉树上每个节点 $p$ 求出 $\textit{rootSum}(p,\textit{targetSum})$，然后对这些路径数目求和即为返回结果。
+ 我们对节点 $p$ 求 $\textit{rootSum}(p,\textit{targetSum})$ 时，以当前节点 $p$ 为目标路径的起点递归向下进行搜索。假设当前的节点 $p$ 的值为 $\textit{val}$，我们对左子树和右子树进行递归搜索，对节点 $p$ 的左孩子节点 $p_{l}$ 求出 $\textit{rootSum}(p_{l},\textit{targetSum}-\textit{val})$，以及对右孩子节点 $p_{r}$ 求出 $\textit{rootSum}(p_{r},\textit{targetSum}-\textit{val})$。节点 $p$ 的 $\textit{rootSum}(p,\textit{targetSum})$ 即等于 $\textit{rootSum}(p_{l},\textit{targetSum}-\textit{val})$ 与 $\textit{rootSum}(p_{r},\textit{targetSum}-\textit{val})$ 之和，同时我们还需要判断一下当前节点 $p$ 的值是否刚好等于 $\textit{targetSum}$。
+ 我们采用递归遍历二叉树的每个节点 $p$，对节点 $p$ 求 $\textit{rootSum}(p,\textit{val})$，然后将每个节点所有求的值进行相加求和返回。
**代码**
* [sol1-C++]
```C++
class Solution {
public:
int rootSum(TreeNode* root, int targetSum) {
if (!root) {
return 0;
}
int ret = 0;
if (root->val == targetSum) {
ret++;
}
ret += rootSum(root->left, targetSum - root->val);
ret += rootSum(root->right, targetSum - root->val);
return ret;
}
int pathSum(TreeNode* root, int targetSum) {
if (!root) {
return 0;
}
int ret = rootSum(root, targetSum);
ret += pathSum(root->left, targetSum);
ret += pathSum(root->right, targetSum);
return ret;
}
};
```
* [sol1-Java]
```Java
class Solution {
public int pathSum(TreeNode root, int targetSum) {
if (root == null) {
return 0;
}
int ret = rootSum(root, targetSum);
ret += pathSum(root.left, targetSum);
ret += pathSum(root.right, targetSum);
return ret;
}
public int rootSum(TreeNode root, int targetSum) {
int ret = 0;
if (root == null) {
return 0;
}
int val = root.val;
if (val == targetSum) {
ret++;
}
ret += rootSum(root.left, targetSum - val);
ret += rootSum(root.right, targetSum - val);
return ret;
}
}
```
* [sol1-C#]
```C#
public class Solution {
public int PathSum(TreeNode root, int targetSum) {
if (root == null) {
return 0;
}
int ret = RootSum(root, targetSum);
ret += PathSum(root.left, targetSum);
ret += PathSum(root.right, targetSum);
return ret;
}
public int RootSum(TreeNode root, int targetSum) {
int ret = 0;
if (root == null) {
return 0;
}
int val = root.val;
if (val == targetSum) {
ret++;
}
ret += RootSum(root.left, targetSum - val);
ret += RootSum(root.right, targetSum - val);
return ret;
}
}
```
* [sol1-Python3]
```Python
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
def rootSum(root, targetSum):
if root is None:
return 0
ret = 0
if root.val == targetSum:
ret += 1
ret += rootSum(root.left, targetSum - root.val)
ret += rootSum(root.right, targetSum - root.val)
return ret
if root is None:
return 0
ret = rootSum(root, targetSum)
ret += self.pathSum(root.left, targetSum)
ret += self.pathSum(root.right, targetSum)
return ret
```
* [sol1-JavaScript]
```JavaScript
var pathSum = function(root, targetSum) {
if (root == null) {
return 0;
}
let ret = rootSum(root, targetSum);
ret += pathSum(root.left, targetSum);
ret += pathSum(root.right, targetSum);
return ret;
};
const rootSum = (root, targetSum) => {
let ret = 0;
if (root == null) {
return 0;
}
const val = root.val;
if (val === targetSum) {
ret++;
}
ret += rootSum(root.left, targetSum - val);
ret += rootSum(root.right, targetSum - val);
return ret;
}
```
* [sol1-Golang]
```go
func rootSum(root *TreeNode, targetSum int) (res int) {
if root == nil {
return
}
val := root.Val
if val == targetSum {
res++
}
res += rootSum(root.Left, targetSum-val)
res += rootSum(root.Right, targetSum-val)
return
}
func pathSum(root *TreeNode, targetSum int) int {
if root == nil {
return 0
}
res := rootSum(root, targetSum)
res += pathSum(root.Left, targetSum)
res += pathSum(root.Right, targetSum)
return res
}
```
**复杂度分析**
- 时间复杂度：$O(N^2)$，其中 $N$ 为该二叉树节点的个数。对于每一个节点，求以该节点为起点的路径数目时，则需要遍历以该节点为根节点的子树的所有节点，因此求该路径所花费的最大时间为 $O(N)$，我们会对每个节点都求一次以该节点为起点的路径数目，因此时间复杂度为 $O(N^{2})$。
- 空间复杂度：$O(N)$，考虑到递归需要在栈上开辟空间。
#### 方法二: 前缀和
**思路与算法**
我们仔细思考一下，解法一中应该存在许多重复计算。我们定义节点的前缀和为：由根结点到当前结点的路径上所有节点的和。我们利用先序遍历二叉树，记录下根节点 $\textit{root}$ 到当前节点 $p$ 的路径上除当前节点以外所有节点的前缀和，在已保存的路径前缀和中查找是否存在前缀和刚好等于当前节点到根节点的前缀和 $curr$ 减去 $\textit{targetSum}$。
+ 对于空路径我们也需要保存预先处理一下，此时因为空路径不经过任何节点，因此它的前缀和为 $0$。
+ 假设根节点为 $\textit{root}$，我们当前刚好访问节点 $\textit{node}$，则此时从根节点 $\textit{root}$ 到节点 $\textit{node}$ 的路径（无重复节点）刚好为 $\textit{root} \rightarrow p_1 \rightarrow p_2 \rightarrow \ldots \rightarrow p_k \rightarrow \textit{node}$，此时我们可以已经保存了节点 $p_1, p_2, p_3, \ldots, p_k$ 的前缀和，并且计算出了节点 $\textit{node}$ 的前缀和。
+ 假设当前从根节点 $\textit{root}$ 到节点 $\textit{node}$ 的前缀和为 $\textit{curr}$，则此时我们在已保存的前缀和查找是否存在前缀和刚好等于 $\textit{curr} - \textit{targetSum}$。假设从根节点 $\textit{root}$ 到节点 $\textit{node}$ 的路径中存在节点 $p_i$ 到根节点 $\textit{root}$ 的前缀和为 $\textit{curr} - \textit{targetSum}$，则节点 $p_{i+1}$ 到 $\textit{node}$ 的路径上所有节点的和一定为 $\textit{targetSum}$。
+ 我们利用深度搜索遍历树，当我们退出当前节点时，我们需要及时更新已经保存的前缀和。
**代码**
* [sol2-C++]
```C++
class Solution {
public:
unordered_map<long long, int> prefix;
int dfs(TreeNode *root, long long curr, int targetSum) {
if (!root) {
return 0;
}
int ret = 0;
curr += root->val;
if (prefix.count(curr - targetSum)) {
ret = prefix[curr - targetSum];
}
prefix[curr]++;
ret += dfs(root->left, curr, targetSum);
ret += dfs(root->right, curr, targetSum);
prefix[curr]--;
return ret;
}
int pathSum(TreeNode* root, int targetSum) {
prefix[0] = 1;
return dfs(root, 0, targetSum);
}
};
```
* [sol2-Java]
```Java
class Solution {
public int pathSum(TreeNode root, int targetSum) {
HashMap<Long, Integer> prefix = new HashMap<>();
prefix.put(0L, 1);
return dfs(root, prefix, 0, targetSum);
}
public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) {
if (root == null) {
return 0;
}
int ret = 0;
curr += root.val;
ret = prefix.getOrDefault(curr - targetSum, 0);
prefix.put(curr, prefix.getOrDefault(curr, 0) + 1);
ret += dfs(root.left, prefix, curr, targetSum);
ret += dfs(root.right, prefix, curr, targetSum);
prefix.put(curr, prefix.getOrDefault(curr, 0) - 1);
return ret;
}
}
```
* [sol2-C#]
```C#
public class Solution {
public int PathSum(TreeNode root, int targetSum) {
Dictionary<long, int> prefix = new Dictionary<long, int>();
prefix.Add(0, 1);
return DFS(root, prefix, 0, targetSum);
}
public int DFS(TreeNode root, Dictionary<long, int> prefix, long curr, int targetSum) {
if (root == null) {
return 0;
}
int ret = 0;
curr += root.val;
prefix.TryGetValue(curr - targetSum, out ret);
if (prefix.ContainsKey(curr)) {
++prefix[curr];
} else {
prefix.Add(curr, 1);
}
ret += DFS(root.left, prefix, curr, targetSum);
ret += DFS(root.right, prefix, curr, targetSum);
--prefix[curr];
return ret;
}
}
```
* [sol2-Python3]
```Python
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
prefix = collections.defaultdict(int)
prefix[0] = 1
def dfs(root, curr):
if not root:
return 0
ret = 0
curr += root.val
ret += prefix[curr - targetSum]
prefix[curr] += 1
ret += dfs(root.left, curr)
ret += dfs(root.right, curr)
prefix[curr] -= 1
return ret
return dfs(root, 0)
```
* [sol2-JavaScript]
```JavaScript
var pathSum = function(root, targetSum) {
const prefix = new Map();
prefix.set(0, 1);
return dfs(root, prefix, 0, targetSum);
}
const dfs = (root, prefix, curr, targetSum) => {
if (root == null) {
return 0;
}
let ret = 0;
curr += root.val;
ret = prefix.get(curr - targetSum) || 0;
prefix.set(curr, (prefix.get(curr) || 0) + 1);
ret += dfs(root.left, prefix, curr, targetSum);
ret += dfs(root.right, prefix, curr, targetSum);
prefix.set(curr, (prefix.get(curr) || 0) - 1);
return ret;
}
```
* [sol2-Golang]
```go
func pathSum(root *TreeNode, targetSum int) (ans int) {
preSum := map[int64]int{0: 1}
var dfs func(*TreeNode, int64)
dfs = func(node *TreeNode, curr int64) {
if node == nil {
return
}
curr += int64(node.Val)
ans += preSum[curr-int64(targetSum)]
preSum[curr]++
dfs(node.Left, curr)
dfs(node.Right, curr)
preSum[curr]--
return
}
dfs(root, 0)
return
}
```
**复杂度分析**
- 时间复杂度：$O(N)$，其中 $N$ 为二叉树中节点的个数。利用前缀和只需遍历一次二叉树即可。
- 空间复杂度：$O(N)$。

321
src/main/java/leetcode/editor/cn/doc/solution/mai-mai-gu-piao-de-zui-jia-shi-ji-ii-by-leetcode-s.lcv Normal file
View File

@ -0,0 +1,321 @@
### 📺 视频题解
![122. 买卖股票的最佳时机II.mp4](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/solution/mai-mai-gu-piao-de-zui-jia-shi-ji-ii-by-leetcode-s/12582e43-022d-4ed9-834b-2d1142e3a901)
### 📖 文字题解
#### 方法一：动态规划
考虑到「不能同时参与多笔交易」，因此每天交易结束后只可能存在手里有一支股票或者没有股票的状态。
定义状态 $\textit{dp}[i][0]$ 表示第 $i$ 天交易完后手里没有股票的最大利润，$\textit{dp}[i][1]$ 表示第 $i$ 天交易完后手里持有一支股票的最大利润（$i$ 从 $0$ 开始）。
考虑 $\textit{dp}[i][0]$ 的转移方程，如果这一天交易完后手里没有股票，那么可能的转移状态为前一天已经没有股票，即 $\textit{dp}[i-1][0]$，或者前一天结束的时候手里持有一支股票，即 $\textit{dp}[i-1][1]$，这时候我们要将其卖出，并获得 $\textit{prices}[i]$ 的收益。因此为了收益最大化，我们列出如下的转移方程：
$$
\textit[i][0]=\max\{\textit[i-1][0],\textit[i-1][1]+\textit[i]\}
$$
再来考虑 $\textit{dp}[i][1]$，按照同样的方式考虑转移状态，那么可能的转移状态为前一天已经持有一支股票，即 $\textit{dp}[i-1][1]$，或者前一天结束时还没有股票，即 $\textit{dp}[i-1][0]$，这时候我们要将其买入，并减少 $\textit{prices}[i]$ 的收益。可以列出如下的转移方程：
$$
\textit[i][1]=\max\{\textit[i-1][1],\textit[i-1][0]-\textit[i]\}
$$
对于初始状态，根据状态定义我们可以知道第 $0$ 天交易结束的时候 $\textit{dp}[0][0]=0$，$\textit{dp}[0][1]=-\textit{prices}[0]$。
因此，我们只要从前往后依次计算状态即可。由于全部交易结束后，持有股票的收益一定低于不持有股票的收益，因此这时候 $\textit{dp}[n-1][0]$ 的收益必然是大于 $\textit{dp}[n-1][1]$ 的，最后的答案即为 $\textit{dp}[n-1][0]$。
* [sol11-C++]
```C++
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int dp[n][2];
dp[0][0] = 0, dp[0][1] = -prices[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
};
```
* [sol11-Java]
```Java
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
}
```
* [sol11-JavaScript]
```JavaScript
var maxProfit = function(prices) {
const n = prices.length;
const dp = new Array(n).fill(0).map(v => new Array(2).fill(0));
dp[0][0] = 0, dp[0][1] = -prices[0];
for (let i = 1; i < n; ++i) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
};
```
* [sol11-Golang]
```Golang
func maxProfit(prices []int) int {
n := len(prices)
dp := make([][2]int, n)
dp[0][1] = -prices[0]
for i := 1; i < n; i++ {
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
}
return dp[n-1][0]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
```
* [sol11-C]
```C
int maxProfit(int* prices, int pricesSize) {
int dp[pricesSize][2];
dp[0][0] = 0, dp[0][1] = -prices[0];
for (int i = 1; i < pricesSize; ++i) {
dp[i][0] = fmax(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = fmax(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[pricesSize - 1][0];
}
```
注意到上面的状态转移方程中，每一天的状态只与前一天的状态有关，而与更早的状态都无关，因此我们不必存储这些无关的状态，只需要将 $\textit{dp}[i-1][0]$ 和 $\textit{dp}[i-1][1]$ 存放在两个变量中，通过它们计算出 $\textit{dp}[i][0]$ 和 $\textit{dp}[i][1]$ 并存回对应的变量，以便于第 $i+1$ 天的状态转移即可。
* [sol12-C++]
```C++
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
int dp0 = 0, dp1 = -prices[0];
for (int i = 1; i < n; ++i) {
int newDp0 = max(dp0, dp1 + prices[i]);
int newDp1 = max(dp1, dp0 - prices[i]);
dp0 = newDp0;
dp1 = newDp1;
}
return dp0;
}
};
```
* [sol12-Java]
```Java
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int dp0 = 0, dp1 = -prices[0];
for (int i = 1; i < n; ++i) {
int newDp0 = Math.max(dp0, dp1 + prices[i]);
int newDp1 = Math.max(dp1, dp0 - prices[i]);
dp0 = newDp0;
dp1 = newDp1;
}
return dp0;
}
}
```
* [sol12-JavaScript]
```JavaScript
var maxProfit = function(prices) {
const n = prices.length;
let dp0 = 0, dp1 = -prices[0];
for (let i = 1; i < n; ++i) {
let newDp0 = Math.max(dp0, dp1 + prices[i]);
let newDp1 = Math.max(dp1, dp0 - prices[i]);
dp0 = newDp0;
dp1 = newDp1;
}
return dp0;
};
```
* [sol12-Golang]
```Golang
func maxProfit(prices []int) int {
n := len(prices)
dp0, dp1 := 0, -prices[0]
for i := 1; i < n; i++ {
dp0, dp1 = max(dp0, dp1+prices[i]), max(dp1, dp0-prices[i])
}
return dp0
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
```
* [sol12-C]
```C
int maxProfit(int* prices, int pricesSize) {
int dp0 = 0, dp1 = -prices[0];
for (int i = 1; i < pricesSize; ++i) {
int newDp0 = fmax(dp0, dp1 + prices[i]);
int newDp1 = fmax(dp1, dp0 - prices[i]);
dp0 = newDp0;
dp1 = newDp1;
}
return dp0;
}
```
**复杂度分析**
- 时间复杂度：$O(n)$，其中 $n$ 为数组的长度。一共有 $2n$ 个状态，每次状态转移的时间复杂度为 $O(1)$，因此时间复杂度为 $O(2n)=O(n)$。
- 空间复杂度：$O(n)$。我们需要开辟 $O(n)$ 空间存储动态规划中的所有状态。如果使用空间优化，空间复杂度可以优化至 $O(1)$。
#### 方法二：贪心
由于股票的购买没有限制，因此整个问题等价于寻找 $x$ 个**不相交**的区间 $(l_i,r_i]$ 使得如下的等式最大化
$$
\sum_^ a[r_i]-a[l_i]
$$
其中 $l_i$ 表示在第 $l_i$ 天买入，$r_i$ 表示在第 $r_i$ 天卖出。
同时我们注意到对于 $(l_i,r_i]$ 这一个区间贡献的价值 $a[r_i]-a[l_i]$，其实等价于 $(l_i,l_i+1],(l_i+1,l_i+2],\ldots,(r_i-1,r_i]$ 这若干个区间长度为 $1$ 的区间的价值和，即
$$
a[r_i]-a[l_i]=(a[r_i]-a[r_i-1])+(a[r_i-1]-a[r_i-2])+\ldots+(a[l_i+1]-a[l_i])
$$
因此问题可以简化为找 $x$ 个长度为 $1$ 的区间 $(l_i,l_i+1]$ 使得 $\sum_{i=1}^{x} a[l_i+1]-a[l_i]$ 价值最大化。
贪心的角度考虑我们每次选择贡献大于 $0$ 的区间即能使得答案最大化，因此最后答案为
$$
\textit=\sum_^\max\{0,a[i]-a[i-1]\}
$$
其中 $n$ 为数组的长度。
需要说明的是，贪心算法只能用于计算最大利润，**计算的过程并不是实际的交易过程**。
考虑题目中的例子 $[1,2,3,4,5]$，数组的长度 $n=5$，由于对所有的 $1 \le i < n$ 都有 $a[i]>a[i-1]$，因此答案为
$$
\textit=\sum_^a[i]-a[i-1]=4
$$
但是实际的交易过程并不是进行 $4$ 次买入和 $4$ 次卖出，而是在第 $1$ 天买入，第 $5$ 天卖出。
* [sol2-C++]
```C++
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
int n = prices.size();
for (int i = 1; i < n; ++i) {
ans += max(0, prices[i] - prices[i - 1]);
}
return ans;
}
};
```
* [sol2-Java]
```Java
class Solution {
public int maxProfit(int[] prices) {
int ans = 0;
int n = prices.length;
for (int i = 1; i < n; ++i) {
ans += Math.max(0, prices[i] - prices[i - 1]);
}
return ans;
}
}
```
* [sol2-JavaScript]
```JavaScript
var maxProfit = function(prices) {
let ans = 0;
let n = prices.length;
for (let i = 1; i < n; ++i) {
ans += Math.max(0, prices[i] - prices[i - 1]);
}
return ans;
};
```
* [sol2-Golang]
```Golang
func maxProfit(prices []int) (ans int) {
for i := 1; i < len(prices); i++ {
ans += max(0, prices[i]-prices[i-1])
}
return
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
```
* [sol2-C]
```C
int maxProfit(int* prices, int pricesSize) {
int ans = 0;
for (int i = 1; i < pricesSize; ++i) {
ans += fmax(0, prices[i] - prices[i - 1]);
}
return ans;
}
```
**复杂度分析**
- 时间复杂度：$O(n)$，其中 $n$ 为数组的长度。我们只需要遍历一次数组即可。
- 空间复杂度：$O(1)$。只需要常数空间存放若干变量。

23
src/main/java/leetcode/editor/cn/doc/solution/randliang-ci-49chong-ke-neng-qu-40chong-rik1x.lcv Normal file
View File

@ -0,0 +1,23 @@
* []
```c++
class Solution {
public:
int rand10() {
while (1) {
int a = rand7(), b = rand7();
if (a == 1 && (b < 5)) return 1;
if (a == 2 && (b < 5)) return 2;
if (a == 3 && (b < 5)) return 3;
if (a == 4 && (b < 5)) return 4;
if (a == 5 && (b < 5)) return 5;
if (a == 6 && (b < 5)) return 6;
if (a == 7 && (b < 5)) return 7;
if (b == 5 && (a < 5)) return 8;
if (b == 6 && (a < 5)) return 9;
if (b == 7 && (a < 5)) return 10;
}
}
};
```

131
src/main/java/leetcode/editor/cn/doc/solution/shu-zi-zhuan-huan-wei-shi-liu-jin-zhi-sh-2srt.lcv Normal file
View File

@ -0,0 +1,131 @@
#### 方法一：位运算
题目要求将给定的整数 $\textit{num}$ 转换为十六进制数，负整数使用补码运算方法。
在补码运算中，最高位表示符号位，符号位是 $0$ 表示正整数和零，符号位是 $1$ 表示负整数。$32$ 位有符号整数的二进制数有 $32$ 位，由于一位十六进制数对应四位二进制数，因此 $32$ 位有符号整数的十六进制数有 $8$ 位。将 $\textit{num}$ 的二进制数按照四位一组分成 $8$ 组，依次将每一组转换为对应的十六进制数，即可得到 $\textit{num}$ 的十六进制数。
假设二进制数的 $8$ 组从低位到高位依次是第 $0$ 组到第 $7$ 组，则对于第 $i$ 组，可以通过 $(\textit{nums} >> (4 \times i))~\&~\text{0xf}$ 得到该组的值，其取值范围是 $0$ 到 $15$（即十六进制的 $\text{f}$）。将每一组的值转换为十六进制数的做法如下：
- 对于 $0$ 到 $9$，数字本身就是十六进制数；
- 对于 $10$ 到 $15$，将其转换为 $\text{a}$ 到 $\text{f}$ 中的对应字母。
对于负整数，由于最高位一定不是 $0$，因此不会出现前导零。对于零和正整数，可能出现前导零。避免前导零的做法如下：
- 如果 $\textit{num}=0$，则直接返回 $0$；
- 如果 $\textit{num}>0$，则在遍历每一组的值时，从第一个不是 $0$ 的值开始拼接成十六进制数。
* [sol1-Java]
```Java
class Solution {
public String toHex(int num) {
if (num == 0) {
return "0";
}
StringBuffer sb = new StringBuffer();
for (int i = 7; i >= 0; i --) {
int val = (num >> (4 * i)) & 0xf;
if (sb.length() > 0 || val > 0) {
char digit = val < 10 ? (char) ('0' + val) : (char) ('a' + val - 10);
sb.append(digit);
}
}
return sb.toString();
}
}
```
* [sol1-C#]
```C#
public class Solution {
public string ToHex(int num) {
if (num == 0) {
return "0";
}
StringBuilder sb = new StringBuilder();
for (int i = 7; i >= 0; i --) {
int val = (num >> (4 * i)) & 0xf;
if (sb.Length > 0 || val > 0) {
char digit = val < 10 ? (char) ('0' + val) : (char) ('a' + val - 10);
sb.Append(digit);
}
}
return sb.ToString();
}
}
```
* [sol1-JavaScript]
```JavaScript
var toHex = function(num) {
if (num === 0) {
return "0";
}
const sb = [];
for (let i = 7; i >= 0; i --) {
const val = (num >> (4 * i)) & 0xf;
if (sb.length > 0 || val > 0) {
const digit = val < 10 ? String.fromCharCode('0'.charCodeAt() + val) : String.fromCharCode('a'.charCodeAt() + val - 10);
sb.push(digit);
}
}
return sb.join('');
}
```
* [sol1-C++]
```C++
class Solution {
public:
string toHex(int num) {
if (num == 0) {
return "0";
}
string sb;
for (int i = 7; i >= 0; i --) {
int val = (num >> (4 * i)) & 0xf;
if (sb.length() > 0 || val > 0) {
char digit = val < 10 ? (char) ('0' + val) : (char) ('a' + val - 10);
sb.push_back(digit);
}
}
return sb;
}
};
```
* [sol1-Golang]
```go
func toHex(num int) string {
if num == 0 {
return "0"
}
sb := &strings.Builder{}
for i := 7; i >= 0; i-- {
val := num >> (4 * i) & 0xf
if val > 0 || sb.Len() > 0 {
var digit byte
if val < 10 {
digit = '0' + byte(val)
} else {
digit = 'a' + byte(val-10)
}
sb.WriteByte(digit)
}
}
return sb.String()
}
```
**复杂度分析**
- 时间复杂度：$O(k)$，其中 $k$ 是整数的十六进制数的位数，这道题中 $k=8$。无论 $\textit{num}$ 的值是多少，都需要遍历 $\textit{num}$ 的十六进制表示的全部数位。
- 空间复杂度：$O(k)$，其中 $k$ 是整数的十六进制数的位数，这道题中 $k=8$。空间复杂度主要取决于中间结果的存储空间，这道题中需要存储 $\textit{num}$ 的十六进制表示中的除了前导零以外的全部数位。

356
src/main/java/leetcode/editor/cn/doc/solution/si-shu-zhi-he-by-leetcode-solution.lcv Normal file
View File

@ -0,0 +1,356 @@
#### 前言
本题与「[15. 三数之和](https://leetcode-cn.com/problems/3sum/)」相似，解法也相似。
#### 方法一：排序 + 双指针
**思路与算法**
最朴素的方法是使用四重循环枚举所有的四元组，然后使用哈希表进行去重操作，得到不包含重复四元组的最终答案。假设数组的长度是 $n$，则该方法中，枚举的时间复杂度为 $O(n^4)$，去重操作的时间复杂度和空间复杂度也很高，因此需要换一种思路。
为了避免枚举到重复四元组，则需要保证每一重循环枚举到的元素不小于其上一重循环枚举到的元素，且在同一重循环中不能多次枚举到相同的元素。
为了实现上述要求，可以对数组进行排序，并且在循环过程中遵循以下两点：
- 每一种循环枚举到的下标必须大于上一重循环枚举到的下标；
- 同一重循环中，如果当前元素与上一个元素相同，则跳过当前元素。
使用上述方法，可以避免枚举到重复四元组，但是由于仍使用四重循环，时间复杂度仍是 $O(n^4)$。注意到数组已经被排序，因此可以使用双指针的方法去掉一重循环。
使用两重循环分别枚举前两个数，然后在两重循环枚举到的数之后使用双指针枚举剩下的两个数。假设两重循环枚举到的前两个数分别位于下标 $i$ 和 $j$，其中 $i<j$。初始时，左右指针分别指向下标 $j+1$ 和下标 $n-1$。每次计算四个数的和，并进行如下操作：
- 如果和等于 $\textit{target}$，则将枚举到的四个数加到答案中，然后将左指针右移直到遇到不同的数，将右指针左移直到遇到不同的数；
- 如果和小于 $\textit{target}$，则将左指针右移一位；
- 如果和大于 $\textit{target}$，则将右指针左移一位。
使用双指针枚举剩下的两个数的时间复杂度是 $O(n)$，因此总时间复杂度是 $O(n^3)$，低于 $O(n^4)$。
具体实现时，还可以进行一些剪枝操作：
- 在确定第一个数之后，如果 $\textit{nums}[i]+\textit{nums}[i+1]+\textit{nums}[i+2]+\textit{nums}[i+3]>\textit{target}$，说明此时剩下的三个数无论取什么值，四数之和一定大于 $\textit{target}$，因此退出第一重循环；
- 在确定第一个数之后，如果 $\textit{nums}[i]+\textit{nums}[n-3]+\textit{nums}[n-2]+\textit{nums}[n-1]<\textit{target}$，说明此时剩下的三个数无论取什么值，四数之和一定小于 $\textit{target}$，因此第一重循环直接进入下一轮，枚举 $\textit{nums}[i+1]$；
- 在确定前两个数之后，如果 $\textit{nums}[i]+\textit{nums}[j]+\textit{nums}[j+1]+\textit{nums}[j+2]>\textit{target}$，说明此时剩下的两个数无论取什么值，四数之和一定大于 $\textit{target}$，因此退出第二重循环；
- 在确定前两个数之后，如果 $\textit{nums}[i]+\textit{nums}[j]+\textit{nums}[n-2]+\textit{nums}[n-1]<\textit{target}$，说明此时剩下的两个数无论取什么值，四数之和一定小于 $\textit{target}$，因此第二重循环直接进入下一轮，枚举 $\textit{nums}[j+1]$。
**代码**
* [sol1-Java]
```Java
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> quadruplets = new ArrayList<List<Integer>>();
if (nums == null || nums.length < 4) {
return quadruplets;
}
Arrays.sort(nums);
int length = nums.length;
for (int i = 0; i < length - 3; i++) {
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
if (nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {
break;
}
if (nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
for (int j = i + 1; j < length - 2; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
if (nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {
break;
}
if (nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
int left = j + 1, right = length - 1;
while (left < right) {
int sum = nums[i] + nums[j] + nums[left] + nums[right];
if (sum == target) {
quadruplets.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
while (left < right && nums[left] == nums[left + 1]) {
left++;
}
left++;
while (left < right && nums[right] == nums[right - 1]) {
right--;
}
right--;
} else if (sum < target) {
left++;
} else {
right--;
}
}
}
}
return quadruplets;
}
}
```
* [sol1-C++]
```C++
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> quadruplets;
if (nums.size() < 4) {
return quadruplets;
}
sort(nums.begin(), nums.end());
int length = nums.size();
for (int i = 0; i < length - 3; i++) {
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
if (nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {
break;
}
if (nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
for (int j = i + 1; j < length - 2; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
if (nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {
break;
}
if (nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
int left = j + 1, right = length - 1;
while (left < right) {
int sum = nums[i] + nums[j] + nums[left] + nums[right];
if (sum == target) {
quadruplets.push_back({nums[i], nums[j], nums[left], nums[right]});
while (left < right && nums[left] == nums[left + 1]) {
left++;
}
left++;
while (left < right && nums[right] == nums[right - 1]) {
right--;
}
right--;
} else if (sum < target) {
left++;
} else {
right--;
}
}
}
}
return quadruplets;
}
};
```
* [sol1-JavaScript]
```JavaScript
var fourSum = function(nums, target) {
const quadruplets = [];
if (nums.length < 4) {
return quadruplets;
}
nums.sort((x, y) => x - y);
const length = nums.length;
for (let i = 0; i < length - 3; i++) {
if (i > 0 && nums[i] === nums[i - 1]) {
continue;
}
if (nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {
break;
}
if (nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
for (let j = i + 1; j < length - 2; j++) {
if (j > i + 1 && nums[j] === nums[j - 1]) {
continue;
}
if (nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {
break;
}
if (nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
let left = j + 1, right = length - 1;
while (left < right) {
const sum = nums[i] + nums[j] + nums[left] + nums[right];
if (sum === target) {
quadruplets.push([nums[i], nums[j], nums[left], nums[right]]);
while (left < right && nums[left] === nums[left + 1]) {
left++;
}
left++;
while (left < right && nums[right] === nums[right - 1]) {
right--;
}
right--;
} else if (sum < target) {
left++;
} else {
right--;
}
}
}
}
return quadruplets;
};
```
* [sol1-Python3]
```Python
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
quadruplets = list()
if not nums or len(nums) < 4:
return quadruplets
nums.sort()
length = len(nums)
for i in range(length - 3):
if i > 0 and nums[i] == nums[i - 1]:
continue
if nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target:
break
if nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target:
continue
for j in range(i + 1, length - 2):
if j > i + 1 and nums[j] == nums[j - 1]:
continue
if nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target:
break
if nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target:
continue
left, right = j + 1, length - 1
while left < right:
total = nums[i] + nums[j] + nums[left] + nums[right]
if total == target:
quadruplets.append([nums[i], nums[j], nums[left], nums[right]])
while left < right and nums[left] == nums[left + 1]:
left += 1
left += 1
while left < right and nums[right] == nums[right - 1]:
right -= 1
right -= 1
elif total < target:
left += 1
else:
right -= 1
return quadruplets
```
* [sol1-Golang]
```Golang
func fourSum(nums []int, target int) (quadruplets [][]int) {
sort.Ints(nums)
n := len(nums)
for i := 0; i < n-3 && nums[i]+nums[i+1]+nums[i+2]+nums[i+3] <= target; i++ {
if i > 0 && nums[i] == nums[i-1] || nums[i]+nums[n-3]+nums[n-2]+nums[n-1] < target {
continue
}
for j := i + 1; j < n-2 && nums[i]+nums[j]+nums[j+1]+nums[j+2] <= target; j++ {
if j > i+1 && nums[j] == nums[j-1] || nums[i]+nums[j]+nums[n-2]+nums[n-1] < target {
continue
}
for left, right := j+1, n-1; left < right; {
if sum := nums[i] + nums[j] + nums[left] + nums[right]; sum == target {
quadruplets = append(quadruplets, []int{nums[i], nums[j], nums[left], nums[right]})
for left++; left < right && nums[left] == nums[left-1]; left++ {
}
for right--; left < right && nums[right] == nums[right+1]; right-- {
}
} else if sum < target {
left++
} else {
right--
}
}
}
}
return
}
```
* [sol1-C]
```C
int comp(const void* a, const void* b) {
return *(int*)a - *(int*)b;
}
int** fourSum(int* nums, int numsSize, int target, int* returnSize, int** returnColumnSizes) {
int** quadruplets = malloc(sizeof(int*) * 1001);
*returnSize = 0;
*returnColumnSizes = malloc(sizeof(int) * 1001);
if (numsSize < 4) {
return quadruplets;
}
qsort(nums, numsSize, sizeof(int), comp);
int length = numsSize;
for (int i = 0; i < length - 3; i++) {
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
if (nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {
break;
}
if (nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
for (int j = i + 1; j < length - 2; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
if (nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {
break;
}
if (nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
int left = j + 1, right = length - 1;
while (left < right) {
int sum = nums[i] + nums[j] + nums[left] + nums[right];
if (sum == target) {
int* tmp = malloc(sizeof(int) * 4);
tmp[0] = nums[i], tmp[1] = nums[j], tmp[2] = nums[left], tmp[3] = nums[right];
(*returnColumnSizes)[(*returnSize)] = 4;
quadruplets[(*returnSize)++] = tmp;
while (left < right && nums[left] == nums[left + 1]) {
left++;
}
left++;
while (left < right && nums[right] == nums[right - 1]) {
right--;
}
right--;
} else if (sum < target) {
left++;
} else {
right--;
}
}
}
}
return quadruplets;
}
```
**复杂度分析**
- 时间复杂度：$O(n^3)$，其中 $n$ 是数组的长度。排序的时间复杂度是 $O(n \log n)$，枚举四元组的时间复杂度是 $O(n^3)$，因此总时间复杂度为 $O(n^3+n\log n)=O(n^3)$。
- 空间复杂度：$O(\log n)$，其中 $n$ 是数组的长度。空间复杂度主要取决于排序额外使用的空间。此外排序修改了输入数组 $\textit{nums}$，实际情况中不一定允许，因此也可以看成使用了一个额外的数组存储了数组 $\textit{nums}$ 的副本并排序，空间复杂度为 $O(n)$。

168
src/main/java/leetcode/editor/cn/doc/solution/suo-you-qi-shu-chang-du-zi-shu-zu-de-he-yoaqu.lcv Normal file
View File

@ -0,0 +1,168 @@
#### 方法一：暴力
最简单的解法是遍历数组 $\textit{arr}$ 中的每个长度为奇数的子数组，计算这些子数组的和。由于只需要计算所有长度为奇数的子数组的和，不需要分别计算每个子数组的和，因此只需要维护一个变量 $\textit{sum}$ 存储总和即可。
实现方面，令数组 $\textit{arr}$ 的长度为 $n$，子数组的开始下标为 $\textit{start}$，长度为 $\textit{length}$，结束下标为 $\textit{end}$，则有 $0 \le \textit{start} \le \textit{end} < n$，$\textit{length} = \textit{end} - \textit{start} + 1$ 为奇数。遍历符合上述条件的子数组，计算所有长度为奇数的子数组的和。
* [sol1-Java]
```Java
class Solution {
public int sumOddLengthSubarrays(int[] arr) {
int sum = 0;
int n = arr.length;
for (int start = 0; start < n; start++) {
for (int length = 1; start + length <= n; length += 2) {
int end = start + length - 1;
for (int i = start; i <= end; i++) {
sum += arr[i];
}
}
}
return sum;
}
}
```
* [sol1-C#]
```C#
public class Solution {
public int SumOddLengthSubarrays(int[] arr) {
int sum = 0;
int n = arr.Length;
for (int start = 0; start < n; start++) {
for (int length = 1; start + length <= n; length += 2) {
int end = start + length - 1;
for (int i = start; i <= end; i++) {
sum += arr[i];
}
}
}
return sum;
}
}
```
**复杂度分析**
- 时间复杂度：$O(n^3)$，其中 $n$ 是数组 $\textit{arr}$ 的长度。长度为奇数的子数组的数量是 $O(n^2)$，对于每个子数组需要 $O(n)$ 的时间计算子数组的和，因此总时间复杂度是 $O(n^3)$。
- 空间复杂度：$O(1)$。
#### 方法二：前缀和
方法一中，对于每个子数组需要使用 $O(n)$ 的时间计算子数组的和。如果能将计算每个子数组的和的时间复杂度从 $O(n)$ 降低到 $O(1)$，则能将总时间复杂度从 $O(n^3)$ 降低到 $O(n^2)$。
为了在 $O(1)$ 的时间内得到每个子数组的和，可以使用前缀和。创建长度为 $n + 1$ 的前缀和数组 $\textit{prefixSums}$，其中 $\textit{prefixSums}[0] = 0$，当 $1 \le i \le n$ 时，$\textit{prefixSums}[i]$ 表示数组 $\textit{arr}$ 从下标 $0$ 到下标 $i - 1$ 的元素和。
得到前缀和数组 $\textit{prefixSums}$ 之后，对于 $0 \le \textit{start} \le \textit{end} < n$，数组 $\textit{arr}$ 的下标范围 $[\textit{start}, \textit{end}]$ 的子数组的和为 $\textit{prefixSums}[\textit{end} + 1] - \textit{prefixSums}[\textit{start}]$，可以在 $O(1)$ 的时间内得到每个子数组的和。
* [sol2-Java]
```Java
class Solution {
public int sumOddLengthSubarrays(int[] arr) {
int n = arr.length;
int[] prefixSums = new int[n + 1];
for (int i = 0; i < n; i++) {
prefixSums[i + 1] = prefixSums[i] + arr[i];
}
int sum = 0;
for (int start = 0; start < n; start++) {
for (int length = 1; start + length <= n; length += 2) {
int end = start + length - 1;
sum += prefixSums[end + 1] - prefixSums[start];
}
}
return sum;
}
}
```
* [sol2-C#]
```C#
public class Solution {
public int SumOddLengthSubarrays(int[] arr) {
int n = arr.Length;
int[] prefixSums = new int[n + 1];
for (int i = 0; i < n; i++) {
prefixSums[i + 1] = prefixSums[i] + arr[i];
}
int sum = 0;
for (int start = 0; start < n; start++) {
for (int length = 1; start + length <= n; length += 2) {
int end = start + length - 1;
sum += prefixSums[end + 1] - prefixSums[start];
}
}
return sum;
}
}
```
**复杂度分析**
- 时间复杂度：$O(n^2)$，其中 $n$ 是数组 $\textit{arr}$ 的长度。需要 $O(n)$ 的时间计算前缀和数组 $\textit{prefixSums}$，长度为奇数的子数组的数量是 $O(n^2)$，对于每个子数组需要 $O(1)$ 的时间计算子数组的和，因此总时间复杂度是 $O(n^2)$。
- 空间复杂度：$O(n)$，其中 $n$ 是数组 $\textit{arr}$ 的长度。需要创建长度为 $n + 1$ 的前缀和数组 $\textit{prefixSums}$。
#### 方法三：数学
方法一和方法二都是通过计算每个子数组的和得到所有奇数长度子数组的和。可以换一种思路，数组中的每个元素都会在一个或多个奇数长度的子数组中出现，如果可以计算出每个元素在多少个长度为奇数的子数组中出现，即可得到所有奇数长度子数组的和。
对于元素 $\textit{arr}[i]$，记其左边和右边的元素个数分别为 $\textit{leftCount}$ 和 $\textit{rightCount}$，则 $\textit{leftCount} = i$，$\textit{rightCount} = n - i - 1$。如果元素 $\textit{arr}[i]$ 在一个长度为奇数的子数组中，则在该子数组中，元素 $\textit{arr}[i]$ 的左边和右边的元素个数一定同为奇数或同为偶数（注意 $0$ 也是偶数）。
- 当元素 $\textit{arr}[i]$ 的左边和右边的元素个数同为奇数时，在区间 $[0, \textit{leftCount}]$ 范围内的奇数有 $\textit{leftOdd} = \Big\lfloor \dfrac{\textit{leftCount} + 1}{2} \Big\rfloor$ 个，在区间 $[0, \textit{rightCount}]$ 范围内的奇数有 $\textit{rightOdd} = \Big\lfloor \dfrac{\textit{rightCount} + 1}{2} \Big\rfloor$ 个，包含元素 $\textit{arr}[i]$ 的子数组个数为 $\textit{leftOdd} \times \textit{rightOdd}$；
- 当元素 $\textit{arr}[i]$ 的左边和右边的元素个数同为偶数时，在区间 $[0, \textit{leftCount}]$ 范围内的偶数有 $\textit{leftEven} = \Big\lfloor \dfrac{\textit{leftCount}}{2} \Big\rfloor + 1$ 个，在区间 $[0, \textit{rightCount}]$ 范围内的偶数有 $\textit{rightEven} = \Big\lfloor \dfrac{\textit{rightCount}}{2} \Big\rfloor + 1$ 个，包含元素 $\textit{arr}[i]$ 的子数组个数为 $\textit{leftEven} \times \textit{rightEven}$。
根据上述分析可知，包含元素 $\textit{arr}[i]$ 的奇数长度子数组个数为 $\textit{leftOdd} \times \textit{rightOdd} + \textit{leftEven} \times \textit{rightEven}$，因此元素 $\textit{arr}[i]$ 对奇数长度子数组元素和的贡献为 $\textit{arr}[i] \times (\textit{leftOdd} \times \textit{rightOdd} + \textit{leftEven} \times \textit{rightEven})$。
* [sol3-Java]
```Java
class Solution {
public int sumOddLengthSubarrays(int[] arr) {
int sum = 0;
int n = arr.length;
for (int i = 0; i < n; i++) {
int leftCount = i, rightCount = n - i - 1;
int leftOdd = (leftCount + 1) / 2;
int rightOdd = (rightCount + 1) / 2;
int leftEven = leftCount / 2 + 1;
int rightEven = rightCount / 2 + 1;
sum += arr[i] * (leftOdd * rightOdd + leftEven * rightEven);
}
return sum;
}
}
```
* [sol3-C#]
```C#
public class Solution {
public int SumOddLengthSubarrays(int[] arr) {
int sum = 0;
int n = arr.Length;
for (int i = 0; i < n; i++) {
int leftCount = i, rightCount = n - i - 1;
int leftOdd = (leftCount + 1) / 2;
int rightOdd = (rightCount + 1) / 2;
int leftEven = leftCount / 2 + 1;
int rightEven = rightCount / 2 + 1;
sum += arr[i] * (leftOdd * rightOdd + leftEven * rightEven);
}
return sum;
}
}
```
**复杂度分析**
- 时间复杂度：$O(n)$，其中 $n$ 是数组 $\textit{arr}$ 的长度。需要遍历数组 $\textit{arr}$ 一次，对于每个元素，需要 $O(1)$ 的时间计算该元素在奇数长度子数组的和中的贡献值，因此总时间复杂度是 $O(n)$。
- 空间复杂度：$O(1)$。

204
src/main/java/leetcode/editor/cn/doc/solution/tao-tuo-zu-ai-zhe-by-leetcode-solution-gjga.lcv Normal file
View File

@ -0,0 +1,204 @@
#### 方法一：曼哈顿距离
为了逃脱阻碍者，玩家应按照最短路径向目的地移动。阻碍者为了抓住玩家，也会按照最短路径向目的地移动。由于每次移动为向四个方向之一移动一个单位，因此对于玩家和阻碍者而言，到达目的地的最短路径的距离为当前所在位置和目的地的曼哈顿距离。
用 $\text{dist}(A, B)$ 表示 $A$ 点和 $B$ 点的曼哈顿距离，曼哈顿距离的计算方法如下：
$$
\text(A, B) = \big| x_A - x_B \big| + \big| y_A - y_B \big|
$$
如果有一个阻碍者和目的地的曼哈顿距离小于玩家和目的地的曼哈顿距离，则该阻碍者可以在玩家之前到达目的地，然后停在目的地，玩家无法逃脱。
如果有一个阻碍者和目的地的曼哈顿距离等于玩家和目的地的曼哈顿距离，则该阻碍者可以和玩家同时到达目的地，玩家也无法逃脱。
如果所有的阻碍者和目的地的曼哈顿距离都大于玩家和目的地的曼哈顿距离，则玩家可以在阻碍者之前到达目的地。
如果玩家可以在阻碍者之前到达目的地，是否可能出现阻碍者在玩家前往目的地的中途拦截？答案是否定的，证明如下。
> 假设目的地是 $T$，初始时玩家位于 $S$，阻碍者位于 $G$，阻碍者在 $X$ 点拦截玩家。
>
> 由于阻碍者和目的地的曼哈顿距离大于玩家和目的地的曼哈顿距离，因此 $\text{dist}(G, T) > \text{dist}(S, T)$。
>
> 由于玩家会按照最短路径向目的地移动，因此如果阻碍者在 $X$ 点拦截玩家，则 $X$ 点一定在玩家前往目的地的最短路径上，满足 $\text{dist}(S, X) + \text{dist}(X, T) = \text{dist}(S, T)$。
>
> 由于 $X$ 点是拦截点，因此阻碍者到达 $X$ 点的时间早于或等于玩家到达 $X$ 点的时间，即 $\text{dist}(G, X) \le \text{dist}(S, X)$。
>
> 因此有：
>
> $$
> \begin
> \text(G, X) &\le \text(S, X) \\
> \text(G, X) + \text(X, T) &\le \text(S, X) + \text(X, T) \\
> \text(G, X) + \text(X, T) &\le \text(S, T)
> \end
> $$
>
> 由于阻碍者到目的地的最短路径长度是 $\text{dist}(G, T)$，因此有
>
> $$
> \text(G, T) \le \text(G, X) + \text(X, T) \le \text(S, T)
> $$
>
> 和条件 $\text{dist}(G, T) > \text{dist}(S, T)$ 矛盾。
>
> 因此当 $\text{dist}(G, T) > \text{dist}(S, T)$ 时，阻碍者不可能在玩家前往目的地的中途拦截，玩家可以成功逃脱。
基于上述分析，问题简化为计算玩家和目的地的曼哈顿距离以及每个阻碍者和目的地的曼哈顿距离，判断玩家是否可以在阻碍者之前到达目的地。
- 如果存在至少一个阻碍者和目的地的曼哈顿距离小于或等于玩家和目的地的曼哈顿距离，返回 $\text{false}$；
- 如果所有阻碍者和目的地的曼哈顿距离都大于玩家和目的地的曼哈顿距离，返回 $\text{true}$。
* [sol1-Java]
```Java
class Solution {
public boolean escapeGhosts(int[][] ghosts, int[] target) {
int[] source = {0, 0};
int distance = manhattanDistance(source, target);
for (int[] ghost : ghosts) {
int ghostDistance = manhattanDistance(ghost, target);
if (ghostDistance <= distance) {
return false;
}
}
return true;
}
public int manhattanDistance(int[] point1, int[] point2) {
return Math.abs(point1[0] - point2[0]) + Math.abs(point1[1] - point2[1]);
}
}
```
* [sol1-C#]
```C#
public class Solution {
public bool EscapeGhosts(int[][] ghosts, int[] target) {
int[] source = {0, 0};
int distance = ManhattanDistance(source, target);
foreach (int[] ghost in ghosts) {
int ghostDistance = ManhattanDistance(ghost, target);
if (ghostDistance <= distance) {
return false;
}
}
return true;
}
public int ManhattanDistance(int[] point1, int[] point2) {
return Math.Abs(point1[0] - point2[0]) + Math.Abs(point1[1] - point2[1]);
}
}
```
* [sol1-JavaScript]
```JavaScript
var escapeGhosts = function(ghosts, target) {
const source = [0, 0];
const distance = manhattanDistance(source, target);
for (const ghost of ghosts) {
const ghostDistance = manhattanDistance(ghost, target);
if (ghostDistance <= distance) {
return false;
}
}
return true;
}
const manhattanDistance = (point1, point2) => {
return Math.abs(point1[0] - point2[0]) + Math.abs(point1[1] - point2[1]);
}
```
* [sol1-Python3]
```Python
class Solution:
def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:
source = [0, 0]
distance = manhattanDistance(source, target)
return all(manhattanDistance(ghost, target) > distance for ghost in ghosts)
def manhattanDistance(point1: List[int], point2: List[int]) -> int:
return abs(point1[0] - point2[0]) + abs(point1[1] - point2[1])
```
* [sol1-Golang]
```go
func escapeGhosts(ghosts [][]int, target []int) bool {
source := []int{0, 0}
distance := manhattanDistance(source, target)
for _, ghost := range ghosts {
if manhattanDistance(ghost, target) <= distance {
return false
}
}
return true
}
func manhattanDistance(point1, point2 []int) int {
return abs(point1[0]-point2[0]) + abs(point1[1]-point2[1])
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
```
* [sol1-C++]
```C++
class Solution {
public:
int manhattanDistance(vector<int>& point1, vector<int>& point2) {
return abs(point1[0] - point2[0]) + abs(point1[1] - point2[1]);
}
bool escapeGhosts(vector<vector<int>>& ghosts, vector<int>& target) {
vector<int> source(2);
int distance = manhattanDistance(source, target);
for (auto& ghost : ghosts) {
int ghostDistance = manhattanDistance(ghost, target);
if (ghostDistance <= distance) {
return false;
}
}
return true;
}
};
```
* [sol1-C]
```C
int manhattanDistance(int* point1, int* point2) {
return abs(point1[0] - point2[0]) + abs(point1[1] - point2[1]);
}
bool escapeGhosts(int** ghosts, int ghostsSize, int* ghostsColSize, int* target, int targetSize) {
int source[2] = {0, 0};
int distance = manhattanDistance(source, target);
for (int i = 0; i < ghostsSize; i++) {
int ghostDistance = manhattanDistance(ghosts[i], target);
if (ghostDistance <= distance) {
return false;
}
}
return true;
}
```
**复杂度分析**
- 时间复杂度：$O(n)$，其中 $n$ 是数组 $\textit{ghosts}$ 的长度。需要计算玩家和目的地的距离，以及遍历数组 $\textit{ghosts}$ 计算每个阻碍者和目的地的距离。
- 空间复杂度：$O(1)$。

43
src/main/java/leetcode/editor/cn/doc/solution/tong-pai-xu-onjie-fa-shuang-bai-by-fszha-9zfo.lcv Normal file
View File

@ -0,0 +1,43 @@
![image.png](https://pic.leetcode-cn.com/1616408484-PFxGNt-image.png)
从题中所给条件出发，0 <= nums[i] <= 5000，5000并不是一个很大的数字，因此可以考虑用桶排序。
步骤：
1、通过桶排序，一次扫描完成排序
2、将桶中数字穿插放入nums中。注释比较详细，直接看代码。
*
```
class Solution {
public void wiggleSort(int[] nums) {
int[]bucket=new int[5001];
for(int num:nums)bucket[num]++;
int len=nums.length;
int small,big;//穿插数字时的上界
//总长度为奇数时，“小 大 小 大 小”边界左右都为较小的数；
//总长度为偶数时，“小 大 小 大”边界左为较小的数，边界右为较大的数
if((len&1)==1){
small=len-1;
big=len-2;
}else{
small=len-2;
big=len-1;
}
int j=5000; //从后往前，将桶中数字穿插到数组中，后界为j
//桶中大的数字在后面，小的数字在前面，所以先取出较大的数字，再取出较小的数字
//先将桶中的较大的数字穿插放在nums中
for(int i=1;i<=big;i+=2){
while (bucket[j]==0)j--;//找到不为0的桶
nums[i]=j;
bucket[j]--;
}
//再将桶中的较小的数字穿插放在nums中
for(int i=0;i<=small;i+=2){
while (bucket[j]==0)j--;//找到不为0的桶
nums[i]=j;
bucket[j]--;
}
}
}
```
如果题解对您有帮助，请点一个赞，谢谢！

113
src/main/java/leetcode/editor/cn/doc/solution/xiang-xi-si-lu-ji-you-hua-si-lu-fen-xi-zhu-xing-ji.lcv Normal file
View File

@ -0,0 +1,113 @@
#### 解题思路
##### 从 rand10() 到 rand7()
如果题目是给你 $rand10()$，让你生成 $1～7$ 之间的某个数，那非常好办，我们只要不断调用 $rand10()$ 即可，直到得到我们要的数，但是为什么可以呢？你可能会怀疑这个是不是等概率的，我们来计算一下
- 如果第一次就 $rand$ 到 $1～7$ 之间的数，那就是直接命中了，概率为 $\frac{1}{10}$
- 如果第二次命中,那么第一次必定没命中，没命中的概率为 $\frac{3}{10}$ ，再乘命中的概率 $\frac{1}{10}$ ，所以第二次命中的概率是 $\frac{1}{10}*\frac{3}{10}$
依次类推，我们求和，可以得到如下结果，可以知道，从 $rand10()$ 到 $rand7()$ 它是等概率的
![image.png](https://pic.leetcode-cn.com/13662225e7f9704ff4475d2a539c7228028ec61d3762f94fb833d29fb237c808-image.png)
##### 从 rand7() 到 rand10()
现在要从 $rand7()$ 到 $rand10()$，也要求是等概率的，那只要我们把小的数映射到一个大的数就好办了，那首先想到的办法是乘个两倍试一试，每个 $rand7()$ 它能生成数的范围是 $1～7$，$rand$ 两次，那么数的范围就变为 $2～14$，哦，你可能发现没有 $1$ 了，想要再减去个 $1$ 来弥补，$rand7()\ +\ rand7() - \ 1$，其实这样是错误的做法，因为对于数字 $5$ 这种，你有两种组合方式 $(2+3\ or\ 3+2)$，而对于 $14$，你只有一种组合方式$(7+7)$，它并不是等概率的，那么简单的加减法不能使用，因为它会使得概率不一致，我们的方法是利用乘法，一般思路如下面这样构建：
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad (rand7() - 1)*7+rand7()$
- 首先 $rand7()-1$ 得到的数的集合为 $\left\{ 0,1,2,3,4,5,6 \right\}$
- 再乘 $7$ 后得到的集合 $A$ 为 $\left\{ 0，7，14，21，28，35，42\right\}$
- 后面 $rand7()$ 得到的集合B为 $\left\{ 1,2,3,4,5,6,7\right\}$
有人可能会疑惑，你咋不乘 $6$，乘 $5$ 呢？因为它不是等概率生成，只有乘 $7$ 才能使得结果是等概率生成的，啥意思？我们得到的集合 $A$ 和集合 $B$，利用这两个集合，得到的数的范围是 $1～49$，每个数它显然是等概率出现的，因为这两个事件是独立事件，如果你不懂什么是独立事件，你试着加加看也能体会一点。
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad P(AB) = P(A)*P(B)=$$$\frac{1}{7}\ *\ \frac{1}{7}$
那么我们可以写出下面的代码
* []
```Java
class Solution extends SolBase {
public int rand10() {
// 首先得到一个数
int num = (rand7() - 1) * 7 + rand7();
// 只要它还大于10，那就给我不断生成，因为我只要范围在1-10的，最后直接返回就可以了
while (num > 10){
num = (rand7() - 1) * 7 + rand7();
}
return num;
}
}
```
提交发现跑的很慢
![image.png](https://pic.leetcode-cn.com/6b845e4c71c5d187df9b3be82953a97c207e812800cffea06231708e9a499a38-image.png)
我们来想想为什么
这样的一个问题是，我们的函数会得到 $1～49$ 之间的数，而我们只想得到 $1～10$ 之间的数，这一部分占的比例太少了，简而言之，这样效率太低，太慢，可能要 $while$ 循环很多次，那么解决思路就是舍弃一部分数，舍弃 $41～49$，因为是独立事件，我们生成的 $1～40$ 之间的数它是等概率的，我们最后完全可以利用 $1～40$ 之间的数来得到 $1～10$ 之间的数。所以，我们的代码可以改成下面这样
* []
```Java
public int rand10() {
// 首先得到一个数
int num = (rand7() - 1) * 7 + rand7();
// 只要它还大于40，那你就给我不断生成吧
while (num > 40)
num = (rand7() - 1) * 7 + rand7();
// 返回结果，+1是为了解决 40%10为0的情况
return 1 + num % 10;
}
```
![image.png](https://pic.leetcode-cn.com/8582eef1938e2d3e75e7e1717ab61871b180551b7b9b665cc2fe26207caec44c-image.png)
##### 再优化
更进一步，这时候我们舍弃了 $9$ 个数，舍弃的还是有点多，效率还是不高，怎么提高效率呢？那就是舍弃的数最好再少一点！因为这样能让 $while$ 循环少转几次，那么对于大于 $40$ 的随机数，别舍弃呀，利用这 $9$ 个数，再利用那个公式操作一下：
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad (大于40的随机数 - 40 - 1) * 7 + rand7()$
这样我们可以得到 $1-63$ 之间的随机数，只要舍弃 $3$ 个即可，那对于这 $3$ 个舍弃的，还可以再来一轮：
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad (大于60的随机数 - 60 - 1) * 7 + rand7()$
这样我们可以得到 $1-21$ 之间的随机数，只要舍弃 $1$ 个即可。
* []
```Java
/**
* The rand7() API is already defined in the parent class SolBase.
* public int rand7();
* @return a random integer in the range 1 to 7
*/
class Solution extends SolBase {
public int rand10() {
while (true){
int num = (rand7() - 1) * 7 + rand7();
// 如果在40以内，那就直接返回
if(num <= 40) return 1 + num % 10;
// 说明刚才生成的在41-49之间，利用随机数再操作一遍
num = (num - 40 - 1) * 7 + rand7();
if(num <= 60) return 1 + num % 10;
// 说明刚才生成的在61-63之间，利用随机数再操作一遍
num = (num - 60 - 1) * 7 + rand7();
if(num <= 20) return 1 + num % 10;
}
}
}
```
提交发现，本来是9ms，结果只要6ms了～
![image.png](https://pic.leetcode-cn.com/864308cff322f7d32a9b3b44dc89c2c4ec4ebc418f4f5619b1697677e612da65-image.png)
希望我的题解对您有帮助～～

34
src/main/java/leetcode/editor/cn/doc/solution/you-xian-dui-lie-zhu-yi-yi-chu-by-ddwuya-l3ua.lcv Normal file
View File

@ -0,0 +1,34 @@
### 解题思路
遇见负数先加上再说，同时保存在最小堆里面
如果此时血量不是正数了，那么就从堆中拿出最小的一个放到最后，同时更新血量
### 代码
* java
```java
class Solution {
public int magicTower(int[] nums) {
int n = nums.length;
Queue<Integer> queue = new PriorityQueue<>();
long cur = 1, sum = 1;
int ans = 0;
for(int i = 0;i < n;i++){
sum += nums[i];
if(nums[i] < 0){
queue.offer(nums[i]);
cur += nums[i];
if(cur <= 0){
cur -= queue.poll();
ans++;
}
}else{
cur += nums[i];
}
}
return sum > 0 ? ans : -1;
}
}
```

577
src/main/java/leetcode/editor/cn/doc/solution/you-xiao-de-gua-hao-zi-fu-chuan-by-leetc-osi3.lcv Normal file
View File

@ -0,0 +1,577 @@
#### 方法一：动态规划
要判断 $s$ 是否为有效的括号字符串，需要判断 $s$ 的首尾字符以及 $s$ 的中间字符是否符合有效的括号字符串的要求。可以使用动态规划求解。
假设字符串 $s$ 的长度为 $n$。定义 $\textit{dp}[i][j]$ 表示字符串 $s$ 从下标 $i$ 到 $j$ 的子串是否为有效的括号字符串，其中 $0 \le i \le j < n$。
动态规划的边界情况是子串的长度为 $1$ 或 $2$ 的情况。
- 当子串的长度为 $1$ 时，只有当该字符是 $\text{`*'}$ 时，才是有效的括号字符串，此时子串可以看成空字符串；
- 当子串的长度为 $2$ 时，只有当两个字符是 $\text{``()"}, \text{``(*"}, \text{``*)"}, \text{``**"}$ 中的一种情况时，才是有效的括号字符串，此时子串可以看成 $\text{``()"}$。
当子串的长度大于 $2$ 时，需要根据子串的首尾字符以及中间的字符判断子串是否为有效的括号字符串。字符串 $s$ 从下标 $i$ 到 $j$ 的子串的长度大于 $2$ 等价于 $j - i \ge 2$，此时 $\textit{dp}[i][j]$ 的计算如下，只要满足以下一个条件就有 $\textit{dp}[i][j] = \text{true}$：
- 如果 $s[i]$ 和 $s[j]$ 分别为左括号和右括号，或者为 $\text{`*'}$，则当 $\textit{dp}[i + 1][j - 1] = \text{true}$ 时，$\textit{dp}[i][j] = \text{true}$，此时 $s[i]$ 和 $s[j]$ 可以分别看成左括号和右括号；
- 如果存在 $i \le k < j$ 使得 $\textit{dp}[i][k]$ 和 $\textit{dp}[k + 1][j]$ 都为 $\textit{true}$，则 $\textit{dp}[i][j] = \text{true}$，因为字符串 $s$ 的下标范围 $[i, k]$ 和 $[k + 1, j]$ 的子串分别为有效的括号字符串，将两个子串拼接之后的子串也为有效的括号字符串，对应下标范围 $[i, j]$。
上述计算过程为从较短的子串的结果得到较长的子串的结果，因此需要注意动态规划的计算顺序。最终答案为 $\textit{dp}[0][n - 1]$。
* [sol1-Java]
```Java
class Solution {
public boolean checkValidString(String s) {
int n = s.length();
boolean[][] dp = new boolean[n][n];
for (int i = 0; i < n; i++) {
if (s.charAt(i) == '*') {
dp[i][i] = true;
}
}
for (int i = 1; i < n; i++) {
char c1 = s.charAt(i - 1), c2 = s.charAt(i);
dp[i - 1][i] = (c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*');
}
for (int i = n - 3; i >= 0; i--) {
char c1 = s.charAt(i);
for (int j = i + 2; j < n; j++) {
char c2 = s.charAt(j);
if ((c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*')) {
dp[i][j] = dp[i + 1][j - 1];
}
for (int k = i; k < j && !dp[i][j]; k++) {
dp[i][j] = dp[i][k] && dp[k + 1][j];
}
}
}
return dp[0][n - 1];
}
}
```
* [sol1-C#]
```C#
public class Solution {
public bool CheckValidString(string s) {
int n = s.Length;
bool[,] dp = new bool[n, n];
for (int i = 0; i < n; i++) {
if (s[i] == '*') {
dp[i, i] = true;
}
}
for (int i = 1; i < n; i++) {
char c1 = s[i - 1], c2 = s[i];
dp[i - 1, i] = (c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*');
}
for (int i = n - 3; i >= 0; i--) {
char c1 = s[i];
for (int j = i + 2; j < n; j++) {
char c2 = s[j];
if ((c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*')) {
dp[i, j] = dp[i + 1, j - 1];
}
for (int k = i; k < j && !dp[i, j]; k++) {
dp[i, j] = dp[i, k] && dp[k + 1, j];
}
}
}
return dp[0, n - 1];
}
}
```
* [sol1-JavaScript]
```JavaScript
var checkValidString = function(s) {
const n = s.length;
const dp = new Array(n).fill(0).map(() => new Array(n).fill(false));
for (let i = 0; i < n; i++) {
if (s[i] === '*') {
dp[i][i] = true;
}
}
for (let i = 1; i < n; i++) {
const c1 = s[i - 1], c2 = s[i];
dp[i - 1][i] = (c1 === '(' || c1 === '*') && (c2 === ')' || c2 === '*');
}
for (let i = n - 3; i >= 0; i--) {
const c1 = s[i];
for (let j = i + 2; j < n; j++) {
const c2 = s[j];
if ((c1 === '(' || c1 === '*') && (c2 === ')' || c2 === '*')) {
dp[i][j] = dp[i + 1][j - 1];
}
for (let k = i; k < j && !dp[i][j]; k++) {
dp[i][j] = dp[i][k] && dp[k + 1][j];
}
}
}
return dp[0][n - 1];
};
```
* [sol1-C++]
```C++
class Solution {
public:
bool checkValidString(string s) {
int n = s.size();
vector<vector<bool>> dp = vector<vector<bool>>(n,vector<bool>(n,false));
for (int i = 0; i < n; i++) {
if (s[i] == '*') {
dp[i][i] = true;
}
}
for (int i = 1; i < n; i++) {
char c1 = s[i - 1];
char c2 = s[i];
dp[i - 1][i] = (c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*');
}
for (int i = n - 3; i >= 0; i--) {
char c1 = s[i];
for (int j = i + 2; j < n; j++) {
char c2 = s[j];
if ((c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*')) {
dp[i][j] = dp[i + 1][j - 1];
}
for (int k = i; k < j && !dp[i][j]; k++) {
dp[i][j] = dp[i][k] && dp[k + 1][j];
}
}
}
return dp[0][n - 1];
}
};
```
* [sol1-Golang]
```go
func checkValidString(s string) bool {
n := len(s)
dp := make([][]bool, n)
for i := range dp {
dp[i] = make([]bool, n)
}
for i, ch := range s {
if ch == '*' {
dp[i][i] = true
}
}
for i := 1; i < n; i++ {
c1, c2 := s[i-1], s[i]
dp[i-1][i] = (c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*')
}
for i := n - 3; i >= 0; i-- {
c1 := s[i]
for j := i + 2; j < n; j++ {
c2 := s[j]
if (c1 == '(' || c1 == '*') && (c2 == ')' || c2 == '*') {
dp[i][j] = dp[i+1][j-1]
}
for k := i; k < j && !dp[i][j]; k++ {
dp[i][j] = dp[i][k] && dp[k+1][j]
}
}
}
return dp[0][n-1]
}
```
**复杂度分析**
- 时间复杂度：$O(n^3)$，其中 $n$ 是字符串 $s$ 的长度。动态规划的状态数是 $O(n^2)$，每个状态的计算时间最多为 $O(n)$。
- 空间复杂度：$O(n^2)$，其中 $n$ 是字符串 $s$ 的长度。创建了 $n$ 行 $n$ 列的二维数组 $\textit{dp}$。
#### 方法二：栈
括号匹配的问题可以用栈求解。
如果字符串中没有星号，则只需要一个栈存储左括号，在从左到右遍历字符串的过程中检查括号是否匹配。
在有星号的情况下，需要两个栈分别存储左括号和星号。从左到右遍历字符串，进行如下操作。
- 如果遇到左括号，则将当前下标存入左括号栈。
- 如果遇到星号，则将当前下标存入星号栈。
- 如果遇到右括号，则需要有一个左括号或星号和右括号匹配，由于星号也可以看成右括号或者空字符串，因此当前的右括号应优先和左括号匹配，没有左括号时和星号匹配：
1. 如果左括号栈不为空，则从左括号栈弹出栈顶元素；
2. 如果左括号栈为空且星号栈不为空，则从星号栈弹出栈顶元素；
3. 如果左括号栈和星号栈都为空，则没有字符可以和当前的右括号匹配，返回 $\text{false}$。
遍历结束之后，左括号栈和星号栈可能还有元素。为了将每个左括号匹配，需要将星号看成右括号，且每个左括号必须出现在其匹配的星号之前。当两个栈都不为空时，每次从左括号栈和星号栈分别弹出栈顶元素，对应左括号下标和星号下标，判断是否可以匹配，匹配的条件是左括号下标小于星号下标，如果左括号下标大于星号下标则返回 $\text{false}$。
最终判断左括号栈是否为空。如果左括号栈为空，则左括号全部匹配完毕，剩下的星号都可以看成空字符串，此时 $s$ 是有效的括号字符串，返回 $\text{true}$。如果左括号栈不为空，则还有左括号无法匹配，此时 $s$ 不是有效的括号字符串，返回 $\text{false}$。
* [sol2-Java]
```Java
class Solution {
public boolean checkValidString(String s) {
Deque<Integer> leftStack = new LinkedList<Integer>();
Deque<Integer> asteriskStack = new LinkedList<Integer>();
int n = s.length();
for (int i = 0; i < n; i++) {
char c = s.charAt(i);
if (c == '(') {
leftStack.push(i);
} else if (c == '*') {
asteriskStack.push(i);
} else {
if (!leftStack.isEmpty()) {
leftStack.pop();
} else if (!asteriskStack.isEmpty()) {
asteriskStack.pop();
} else {
return false;
}
}
}
while (!leftStack.isEmpty() && !asteriskStack.isEmpty()) {
int leftIndex = leftStack.pop();
int asteriskIndex = asteriskStack.pop();
if (leftIndex > asteriskIndex) {
return false;
}
}
return leftStack.isEmpty();
}
}
```
* [sol2-C#]
```C#
public class Solution {
public bool CheckValidString(string s) {
Stack<int> leftStack = new Stack<int>();
Stack<int> asteriskStack = new Stack<int>();
int n = s.Length;
for (int i = 0; i < n; i++) {
char c = s[i];
if (c == '(') {
leftStack.Push(i);
} else if (c == '*') {
asteriskStack.Push(i);
} else {
if (leftStack.Count > 0) {
leftStack.Pop();
} else if (asteriskStack.Count > 0) {
asteriskStack.Pop();
} else {
return false;
}
}
}
while (leftStack.Count > 0 && asteriskStack.Count > 0) {
int leftIndex = leftStack.Pop();
int asteriskIndex = asteriskStack.Pop();
if (leftIndex > asteriskIndex) {
return false;
}
}
return leftStack.Count == 0;
}
}
```
* [sol2-JavaScript]
```JavaScript
var checkValidString = function(s) {
const leftStack = [];
const asteriskStack = [];
const n = s.length;
for (let i = 0; i < n; i++) {
const c = s[i];
if (c === '(') {
leftStack.push(i);
} else if (c === '*') {
asteriskStack.push(i);
} else {
if (leftStack.length) {
leftStack.pop();
} else if (asteriskStack.length) {
asteriskStack.pop();
} else {
return false;
}
}
}
while (leftStack.length && asteriskStack.length) {
const leftIndex = leftStack.pop();
const asteriskIndex = asteriskStack.pop();
if (leftIndex > asteriskIndex) {
return false;
}
}
return leftStack.length === 0;
};
```
* [sol2-C++]
```C++
class Solution {
public:
bool checkValidString(string s) {
stack<int> leftStack;
stack<int> asteriskStack;
int n = s.size();
for (int i = 0; i < n; i++) {
char c = s[i];
if (c == '(') {
leftStack.push(i);
} else if (c == '*') {
asteriskStack.push(i);
} else {
if (!leftStack.empty()) {
leftStack.pop();
} else if (!asteriskStack.empty()) {
asteriskStack.pop();
} else {
return false;
}
}
}
while (!leftStack.empty() && !asteriskStack.empty()) {
int leftIndex = leftStack.top();
leftStack.pop();
int asteriskIndex = asteriskStack.top();
asteriskStack.pop();
if (leftIndex > asteriskIndex) {
return false;
}
}
return leftStack.empty();
}
};
```
* [sol2-Golang]
```go
func checkValidString(s string) bool {
var leftStk, asteriskStk []int
for i, ch := range s {
if ch == '(' {
leftStk = append(leftStk, i)
} else if ch == '*' {
asteriskStk = append(asteriskStk, i)
} else if len(leftStk) > 0 {
leftStk = leftStk[:len(leftStk)-1]
} else if len(asteriskStk) > 0 {
asteriskStk = asteriskStk[:len(asteriskStk)-1]
} else {
return false
}
}
i := len(leftStk) - 1
for j := len(asteriskStk) - 1; i >= 0 && j >= 0; i, j = i-1, j-1 {
if leftStk[i] > asteriskStk[j] {
return false
}
}
return i < 0
}
```
**复杂度分析**
- 时间复杂度：$O(n)$，其中 $n$ 是字符串 $s$ 的长度。需要遍历字符串一次，遍历过程中每个字符的操作时间都是 $O(1)$，遍历结束之后对左括号栈和星号栈弹出元素的操作次数不会超过 $n$。
- 空间复杂度：$O(n)$，其中 $n$ 是字符串 $s$ 的长度。空间复杂度主要取决于左括号栈和星号栈，两个栈的元素总数不会超过 $n$。
#### 方法三：贪心
使用贪心的思想，可以将空间复杂度降到 $O(1)$。
从左到右遍历字符串，遍历过程中，未匹配的左括号数量可能会出现如下变化：
- 如果遇到左括号，则未匹配的左括号数量加 $1$；
- 如果遇到右括号，则需要有一个左括号和右括号匹配，因此未匹配的左括号数量减 $1$；
- 如果遇到星号，由于星号可以看成左括号、右括号或空字符串，因此未匹配的左括号数量可能加 $1$、减 $1$ 或不变。
基于上述结论，可以在遍历过程中维护未匹配的左括号数量可能的最小值和最大值，根据遍历到的字符更新最小值和最大值：
- 如果遇到左括号，则将最小值和最大值分别加 $1$；
- 如果遇到右括号，则将最小值和最大值分别减 $1$；
- 如果遇到星号，则将最小值减 $1$，将最大值加 $1$。
任何情况下，未匹配的左括号数量必须非负，因此当最大值变成负数时，说明没有左括号可以和右括号匹配，返回 $\text{false}$。
当最小值为 $0$ 时，不应将最小值继续减少，以确保最小值非负。
遍历结束时，所有的左括号都应和右括号匹配，因此只有当最小值为 $0$ 时，字符串 $s$ 才是有效的括号字符串。
* [sol3-Java]
```Java
class Solution {
public boolean checkValidString(String s) {
int minCount = 0, maxCount = 0;
int n = s.length();
for (int i = 0; i < n; i++) {
char c = s.charAt(i);
if (c == '(') {
minCount++;
maxCount++;
} else if (c == ')') {
minCount = Math.max(minCount - 1, 0);
maxCount--;
if (maxCount < 0) {
return false;
}
} else {
minCount = Math.max(minCount - 1, 0);
maxCount++;
}
}
return minCount == 0;
}
}
```
* [sol3-C#]
```C#
public class Solution {
public bool CheckValidString(string s) {
int minCount = 0, maxCount = 0;
int n = s.Length;
for (int i = 0; i < n; i++) {
char c = s[i];
if (c == '(') {
minCount++;
maxCount++;
} else if (c == ')') {
minCount = Math.Max(minCount - 1, 0);
maxCount--;
if (maxCount < 0) {
return false;
}
} else {
minCount = Math.Max(minCount - 1, 0);
maxCount++;
}
}
return minCount == 0;
}
}
```
* [sol3-JavaScript]
```JavaScript
var checkValidString = function(s) {
let minCount = 0, maxCount = 0;
const n = s.length;
for (let i = 0; i < n; i++) {
const c = s[i];
if (c === '(') {
minCount++;
maxCount++;
} else if (c === ')') {
minCount = Math.max(minCount - 1, 0);
maxCount--;
if (maxCount < 0) {
return false;
}
} else {
minCount = Math.max(minCount - 1, 0);
maxCount++;
}
}
return minCount === 0;
};
```
* [sol3-C++]
```C++
class Solution {
public:
bool checkValidString(string s) {
int minCount = 0, maxCount = 0;
int n = s.size();
for (int i = 0; i < n; i++) {
char c = s[i];
if (c == '(') {
minCount++;
maxCount++;
} else if (c == ')') {
minCount = max(minCount - 1, 0);
maxCount--;
if (maxCount < 0) {
return false;
}
} else {
minCount = max(minCount - 1, 0);
maxCount++;
}
}
return minCount == 0;
}
};
```
* [sol3-Golang]
```go
func checkValidString(s string) bool {
minCount, maxCount := 0, 0
for _, ch := range s {
if ch == '(' {
minCount++
maxCount++
} else if ch == ')' {
minCount = max(minCount-1, 0)
maxCount--
if maxCount < 0 {
return false
}
} else {
minCount = max(minCount-1, 0)
maxCount++
}
}
return minCount == 0
}
func max(a, b int) int {
if b > a {
return b
}
return a
}
```
**复杂度分析**
- 时间复杂度：$O(n)$，其中 $n$ 是字符串 $s$ 的长度。需要遍历字符串一次。
- 空间复杂度：$O(1)$。

333
src/main/java/leetcode/editor/cn/doc/solution/zhi-you-liang-ge-jian-de-jian-pan-by-lee-ussa.lcv Normal file
View File

@ -0,0 +1,333 @@
#### 方法一：动态规划
**思路与算法**
我们可以使用动态规划的思路解决本题。
设 $f[i]$ 表示打印出 $i$ 个 $\text{A}$ 的最少操作次数。由于我们只能使用「复制全部」和「粘贴」两种操作，那么要想得到 $i$ 个 $\text{A}$，我们必须首先拥有 $j$ 个 $\text{A}$，使用一次「复制全部」操作，再使用若干次「粘贴」操作得到 $i$ 个 $\text{A}$。
因此，这里的 $j$ 必须是 $i$ 的因数，「粘贴」操作的使用次数即为 $\dfrac{i}{j} - 1$。我们可以枚举 $j$ 进行状态转移，这样就可以得到状态转移方程：
$$
f[i] = \min_{j \mid i} \big\{ f[j] + \frac \big\}
$$
其中 $j \mid i$ 表示 $j$ 可以整除 $i$，即 $j$ 是 $i$ 的因数。
动态规划的边界条件为 $f[1] = 0$，最终的答案即为 $f[n]$。
**细节**
在枚举 $i$ 的因数 $j$ 时，我们可以直接在 $O(i)$ 的时间内依次枚举 $[1, i)$。
由于 $i$ 肯定同时拥有因数 $j$ 和 $\dfrac{i}{j}$，二者必有一个小于等于 $\sqrt{i}$。因此，一种时间复杂度更低的方法是，我们只在 $[1, \sqrt{i}]$ 的范围内枚举 $j$，并用 $j$ 和 $\dfrac{i}{j}$ 分别作为因数进行状态转移，时间复杂度为 $O(\sqrt{i})$。
**代码**
* [sol1-C++]
```C++
class Solution {
public:
int minSteps(int n) {
vector<int> f(n + 1);
for (int i = 2; i <= n; ++i) {
f[i] = INT_MAX;
for (int j = 1; j * j <= i; ++j) {
if (i % j == 0) {
f[i] = min(f[i], f[j] + i / j);
f[i] = min(f[i], f[i / j] + j);
}
}
}
return f[n];
}
};
```
* [sol1-Java]
```Java
class Solution {
public int minSteps(int n) {
int[] f = new int[n + 1];
for (int i = 2; i <= n; ++i) {
f[i] = Integer.MAX_VALUE;
for (int j = 1; j * j <= i; ++j) {
if (i % j == 0) {
f[i] = Math.min(f[i], f[j] + i / j);
f[i] = Math.min(f[i], f[i / j] + j);
}
}
}
return f[n];
}
}
```
* [sol1-C#]
```C#
public class Solution {
public int MinSteps(int n) {
int[] f = new int[n + 1];
for (int i = 2; i <= n; ++i) {
f[i] = int.MaxValue;
for (int j = 1; j * j <= i; ++j) {
if (i % j == 0) {
f[i] = Math.Min(f[i], f[j] + i / j);
f[i] = Math.Min(f[i], f[i / j] + j);
}
}
}
return f[n];
}
}
```
* [sol1-Python3]
```Python
class Solution:
def minSteps(self, n: int) -> int:
f = [0] * (n + 1)
for i in range(2, n + 1):
f[i] = float("inf")
j = 1
while j * j <= i:
if i % j == 0:
f[i] = min(f[i], f[j] + i // j)
f[i] = min(f[i], f[i // j] + j)
j += 1
return f[n]
```
* [sol1-Golang]
```go
func minSteps(n int) int {
f := make([]int, n+1)
for i := 2; i <= n; i++ {
f[i] = math.MaxInt32
for j := 1; j*j <= i; j++ {
if i%j == 0 {
f[i] = min(f[i], f[j]+i/j)
f[i] = min(f[i], f[i/j]+j)
}
}
}
return f[n]
}
func min(a, b int) int {
if a > b {
return b
}
return a
}
```
* [sol1-JavaScript]
```JavaScript
var minSteps = function(n) {
const f = new Array(n + 1).fill(0);
for (let i = 2; i <= n; ++i) {
f[i] = Number.MAX_SAFE_INTEGER;
for (let j = 1; j * j <= i; ++j) {
if (i % j === 0) {
f[i] = Math.min(f[i], Math.floor(f[j] + i / j));
f[i] = Math.min(f[i], Math.floor(f[i / j] + j));
}
}
}
return f[n];
};
```
**复杂度分析**
- 时间复杂度：$O(n \sqrt{n})$。
- 空间复杂度：$O(n)$，即为存储所有状态需要的空间。
#### 方法二：分解质因数
**思路与算法**
观察方法一中的状态转移方程：
$$
f[i] = \min_{j \mid i} \big\{ f[j] + \frac \big\}
$$
我们可以转写成等价的形式：
$$
f[i] = \min_{j \mid i} \big\{ f[\frac{i}{j}] + j \big\}
$$
此时状态转移方程就有了直观上的表述，即 $f[n]$ 表示：
> 给定初始值 $n$，我们希望通过若干次操作将其变为 $1$。每次操作我们可以选择 $n$ 的一个大于 $1$ 的因数 $j$，耗费 $j$ 的代价并且将 $n$ 减少为 $\dfrac{n}{j}$。在所有可行的操作序列中，总代价的**最小值**即为 $f[n]$。
我们选择的所有因数的乘积必然为 $n$。因此，我们将 $n$ 拆分成若干个大于 $1$ 的整数的乘积：
$$
n = \alpha_1 \times \alpha_2 \times \cdots \times \alpha_k
$$
那么总代价即为：
$$
\sum_^k \alpha_i
$$
对于任意的 $\alpha_i$，如果其为素数，那么无法继续进行拆分；如果其为合数，那么对于任意一种拆分成两个大于 $1$ 的整数的方式：
$$
\alpha_i = \beta_0 \times \beta_1
$$
拆分前的代价为 $\beta_0 \times \beta_1$，而拆分后的代价为 $\beta_0 + \beta_1$。由于它们均大于 $1$，因此：
$$
\beta_0 + \beta_1 \leq \beta_0 \times \beta_1
$$
恒成立。也就是说，在达到**最小的总代价**时，我们将 $n$ 拆分成了若干个素数的乘积。因此我们只需要对 $n$ 进行质因数分解，统计所有质因数的和，即为最终的答案。
**证明**
当 $\beta_0, \beta_1 > 1$ 时：
$$
\beta_0 \times \beta_1 - (\beta_0 + \beta_1) = (\beta_0 - 1)(\beta_1 - 1) - 1 \geq 0
$$
得证。
**代码**
* [sol2-C++]
```C++
class Solution {
public:
int minSteps(int n) {
int ans = 0;
for (int i = 2; i * i <= n; ++i) {
while (n % i == 0) {
n /= i;
ans += i;
}
}
if (n > 1) {
ans += n;
}
return ans;
}
};
```
* [sol2-Java]
```Java
class Solution {
public int minSteps(int n) {
int ans = 0;
for (int i = 2; i * i <= n; ++i) {
while (n % i == 0) {
n /= i;
ans += i;
}
}
if (n > 1) {
ans += n;
}
return ans;
}
}
```
* [sol2-C#]
```C#
public class Solution {
public int MinSteps(int n) {
int ans = 0;
for (int i = 2; i * i <= n; ++i) {
while (n % i == 0) {
n /= i;
ans += i;
}
}
if (n > 1) {
ans += n;
}
return ans;
}
}
```
* [sol2-Python3]
```Python
class Solution:
def minSteps(self, n: int) -> int:
ans = 0
i = 2
while i * i <= n:
while n % i == 0:
n //= i
ans += i
i += 1
if n > 1:
ans += n
return ans
```
* [sol2-Golang]
```go
func minSteps(n int) (ans int) {
for i := 2; i*i <= n; i++ {
for n%i == 0 {
n /= i
ans += i
}
}
if n > 1 {
ans += n
}
return
}
```
* [sol2-JavaScript]
```JavaScript
var minSteps = function(n) {
let ans = 0;
for (let i = 2; i * i <= n; ++i) {
while (n % i === 0) {
n = Math.floor(n / i);
ans += i;
}
}
if (n > 1) {
ans += n;
}
return ans;
};
```
**复杂度分析**
- 时间复杂度：$O(\sqrt{n})$，即为质因数分解的时间复杂度。
- 空间复杂度：$O(1)$。