101:对称二叉树

src/main/java/leetcode/editor/cn/SymmetricTree.java

@@ -0,0 +1,84 @@
+//给定一个二叉树，检查它是否是镜像对称的。 
+//
+// 
+//
+// 例如，二叉树 [1,2,2,3,4,4,3] 是对称的。 
+//
+//     1
+//   / \
+//  2   2
+// / \ / \
+//3  4 4  3
+// 
+//
+// 
+//
+// 但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的: 
+//
+//     1
+//   / \
+//  2   2
+//   \   \
+//   3    3
+// 
+//
+// 
+//
+// 进阶： 
+//
+// 你可以运用递归和迭代两种方法解决这个问题吗？ 
+// Related Topics 树 深度优先搜索 广度优先搜索 二叉树 👍 1583 👎 0
+
+package leetcode.editor.cn;
+
+import com.code.leet.entiy.TreeNode;
+
+//101:对称二叉树
+class SymmetricTree {
+    public static void main(String[] args) {
+        //测试代码
+        Solution solution = new SymmetricTree().new Solution();
+    }
+
+    //力扣代码
+    //leetcode submit region begin(Prohibit modification and deletion)
+
+    /**
+     * Definition for a binary tree node.
+     * public class TreeNode {
+     * int val;
+     * TreeNode left;
+     * TreeNode right;
+     * TreeNode() {}
+     * TreeNode(int val) { this.val = val; }
+     * TreeNode(int val, TreeNode left, TreeNode right) {
+     * this.val = val;
+     * this.left = left;
+     * this.right = right;
+     * }
+     * }
+     */
+    class Solution {
+        public boolean isSymmetric(TreeNode root) {
+            return dfs(root.left, root.right);
+        }
+
+        private boolean dfs(TreeNode node1, TreeNode node2) {
+            if (node1 == null && node2 == null) {
+                return true;
+            }
+            if (node1 == null || node2 == null) {
+                return false;
+            }
+            if (node1.val != node2.val) {
+                return false;
+            }
+            if (!dfs(node1.left, node2.right)) {
+                return false;
+            }
+            return dfs(node1.right, node2.left);
+        }
+    }
+//leetcode submit region end(Prohibit modification and deletion)
+
+}

src/main/java/leetcode/editor/cn/doc/content/SymmetricTree.md

@@ -0,0 +1,30 @@
+<p>给定一个二叉树，检查它是否是镜像对称的。</p>
+
+<p>&nbsp;</p>
+
+<p>例如，二叉树&nbsp;<code>[1,2,2,3,4,4,3]</code> 是对称的。</p>
+
+<pre>    1
+   / \
+  2   2
+ / \ / \
+3  4 4  3
+</pre>
+
+<p>&nbsp;</p>
+
+<p>但是下面这个&nbsp;<code>[1,2,2,null,3,null,3]</code> 则不是镜像对称的:</p>
+
+<pre>    1
+   / \
+  2   2
+   \   \
+   3    3
+</pre>
+
+<p>&nbsp;</p>
+
+<p><strong>进阶：</strong></p>
+
+<p>你可以运用递归和迭代两种方法解决这个问题吗？</p>
+<div><div>Related Topics</div><div><li>树</li><li>深度优先搜索</li><li>广度优先搜索</li><li>二叉树</li></div></div><br><div><li>👍 1583</li><li>👎 0</li></div>

src/main/java/leetcode/editor/cn/doc/solution/dui-cheng-er-cha-shu-by-leetcode-solution.lcv

@@ -0,0 +1,232 @@
+### 📺 视频题解
+
+![101. 对称二叉树.mp4](https://leetcode-cn.com/problems/symmetric-tree/solution/dui-cheng-er-cha-shu-by-leetcode-solution/d45ef3c2-7ecd-4a10-b1f4-1ea3be6ce8c8)
+
+### 📖 文字题解
+
+#### 方法一：递归
+
+**思路和算法**
+
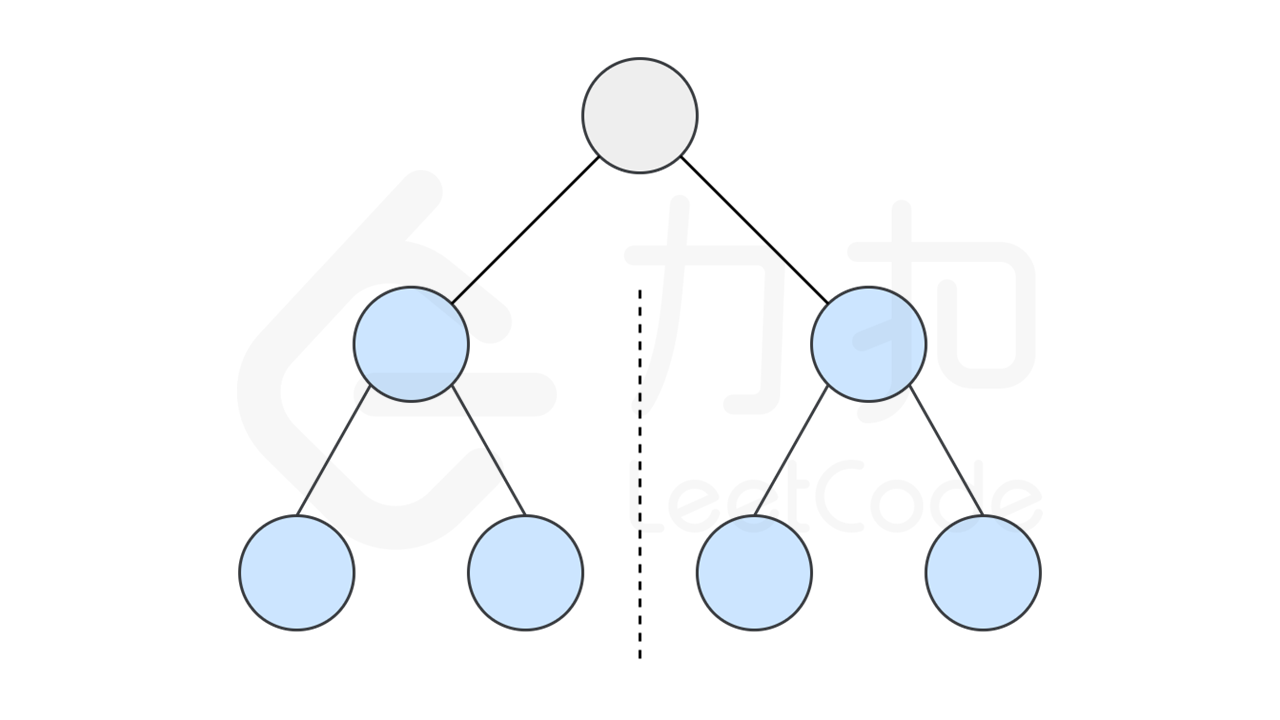
+如果一个树的左子树与右子树镜像对称，那么这个树是对称的。
+
+![fig1](https://assets.leetcode-cn.com/solution-static/101/101_fig1.PNG)
+
+因此，该问题可以转化为：两个树在什么情况下互为镜像？
+
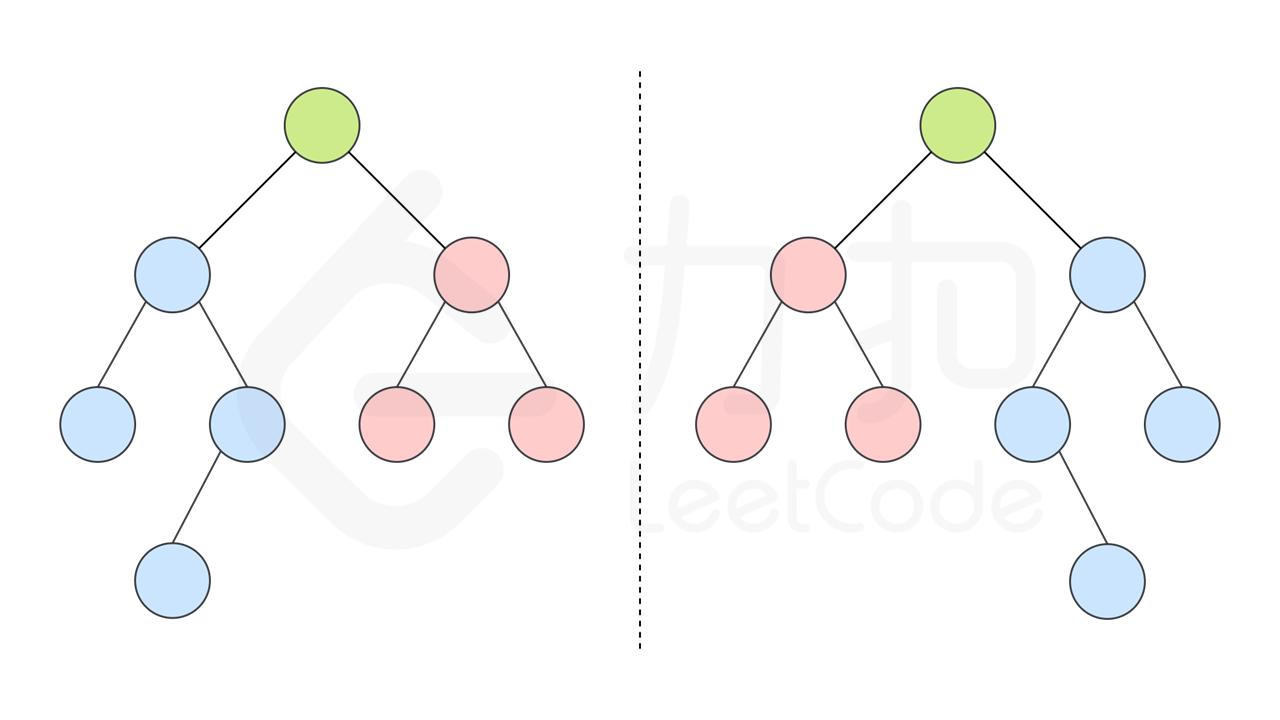
+如果同时满足下面的条件，两个树互为镜像：
+
++ 它们的两个根结点具有相同的值
++ 每个树的右子树都与另一个树的左子树镜像对称
+
+![fig2](https://assets.leetcode-cn.com/solution-static/101/101_fig2.PNG)
+
+我们可以实现这样一个递归函数，通过「同步移动」两个指针的方法来遍历这棵树，$p$ 指针和 $q$ 指针一开始都指向这棵树的根，随后 $p$ 右移时，$q$ 左移，$p$ 左移时，$q$ 右移。每次检查当前 $p$ 和 $q$ 节点的值是否相等，如果相等再判断左右子树是否对称。
+
+代码如下。
+
+* [sol1-C++]
+
+```cpp
+class Solution {
+public:
+    bool check(TreeNode *p, TreeNode *q) {
+        if (!p && !q) return true;
+        if (!p || !q) return false;
+        return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
+    }
+
+    bool isSymmetric(TreeNode* root) {
+        return check(root, root);
+    }
+};
+```
+
+* [sol1-Java]
+
+```Java
+class Solution {
+    public boolean isSymmetric(TreeNode root) {
+        return check(root, root);
+    }
+
+    public boolean check(TreeNode p, TreeNode q) {
+        if (p == null && q == null) {
+            return true;
+        }
+        if (p == null || q == null) {
+            return false;
+        }
+        return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);
+    }
+}
+```
+
+* [sol1-Golang]
+
+```golang
+func isSymmetric(root *TreeNode) bool {
+    return check(root, root)
+}
+
+func check(p, q *TreeNode) bool {
+    if p == nil && q == nil {
+        return true
+    }
+    if p == nil || q == nil {
+        return false
+    }
+    return p.Val == q.Val && check(p.Left, q.Right) && check(p.Right, q.Left) 
+}
+```
+
+* [sol1-TypeScript]
+
+```TypeScript
+const check = (p: TreeNode | null, q: TreeNode | null): boolean => {
+    if (!p && !q) return true;
+    if (!p || !q) return false;
+    return p.val === q.val && check(p.left, q.right) && check(p.right, q.left);
+}
+var isSymmetric = function(root: TreeNode | null): boolean {
+    return check(root, root);
+};
+```
+
+**复杂度分析**
+
+假设树上一共 $n$ 个节点。
+
++ 时间复杂度：这里遍历了这棵树，渐进时间复杂度为 $O(n)$。
++ 空间复杂度：这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 $n$，故渐进空间复杂度为 $O(n)$。
+
+#### 方法二：迭代
+
+**思路和算法**
+
+「方法一」中我们用递归的方法实现了对称性的判断，那么如何用迭代的方法实现呢？首先我们引入一个队列，这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。
+
+* [sol2-C++]
+
+```cpp
+class Solution {
+public:
+    bool check(TreeNode *u, TreeNode *v) {
+        queue <TreeNode*> q;
+        q.push(u); q.push(v);
+        while (!q.empty()) {
+            u = q.front(); q.pop();
+            v = q.front(); q.pop();
+            if (!u && !v) continue;
+            if ((!u || !v) || (u->val != v->val)) return false;
+
+            q.push(u->left); 
+            q.push(v->right);
+
+            q.push(u->right); 
+            q.push(v->left);
+        }
+        return true;
+    }
+
+    bool isSymmetric(TreeNode* root) {
+        return check(root, root);
+    }
+};
+```
+
+* [sol2-Java]
+
+```Java
+class Solution {
+    public boolean isSymmetric(TreeNode root) {
+        return check(root, root);
+    }
+
+    public boolean check(TreeNode u, TreeNode v) {
+        Queue<TreeNode> q = new LinkedList<TreeNode>();
+        q.offer(u);
+        q.offer(v);
+        while (!q.isEmpty()) {
+            u = q.poll();
+            v = q.poll();
+            if (u == null && v == null) {
+                continue;
+            }
+            if ((u == null || v == null) || (u.val != v.val)) {
+                return false;
+            }
+
+            q.offer(u.left);
+            q.offer(v.right);
+
+            q.offer(u.right);
+            q.offer(v.left);
+        }
+        return true;
+    }
+}
+```
+
+* [sol2-Golang]
+
+```golang
+func isSymmetric(root *TreeNode) bool {
+    u, v := root, root
+    q := []*TreeNode{}
+    q = append(q, u)
+    q = append(q, v)
+    for len(q) > 0 {
+        u, v = q[0], q[1]
+        q = q[2:]
+        if u == nil && v == nil {
+            continue
+        }
+        if u == nil || v == nil {
+            return false
+        }
+        if u.Val != v.Val {
+            return false
+        }
+        q = append(q, u.Left)
+        q = append(q, v.Right)
+
+        q = append(q, u.Right)
+        q = append(q, v.Left)
+    }
+    return true
+}
+```
+
+* [sol2-TypeScript]
+
+```TypeScript
+const check = (u: TreeNode | null, v: TreeNode | null): boolean => {
+    const q: (TreeNode | null)[] = [];
+    q.push(u),q.push(v);
+
+    while (q.length) {
+        u = q.shift()!;
+        v = q.shift()!;
+
+        if (!u && !v) continue;
+        if ((!u || !v) || (u.val !== v.val)) return false;
+
+        q.push(u.left); 
+        q.push(v.right);
+
+        q.push(u.right); 
+        q.push(v.left);
+    }
+    return true;
+}
+var isSymmetric = function(root: TreeNode | null): boolean {
+    return check(root, root);
+};
+```
+
+**复杂度分析**
+
++ 时间复杂度：$O(n)$，同「方法一」。
++ 空间复杂度：这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 $n$ 个点，故渐进空间复杂度为 $O(n)$。
+